Experimental Study of Non Linear Second Sound Waves

Experimental Study of Non. Linear Second Sound Waves in He-II Victor Efimov Institute of Solid State Physics RAS, Chernogolovka, Russia; Lancaster University, Lancaster, UK I. Borisenko, O. Griffiths, P. Hendry, G. Kolmakov, A. Kuliev, E. Lebedeva, P. E. V. Mc. Clintock, L. Mezhov-Deglin 9 December 2005 Warwick

Nonlinear second sound waves in superfluid helium 9 December 2005 Warwick 2

Hydrodynamic Equations of Ideal Fluids For any an ideal fluid (incompressible, without energy dissipation) it may be written the equation of continuity (mass conservation) where mass flux density Ø the equation of motion Newton’s second law Ø Ø the equation of adiabatic motion of an ideal fluid the “equation of entropy continuity” where “entropy flux” 9 December 2005 Warwick 3

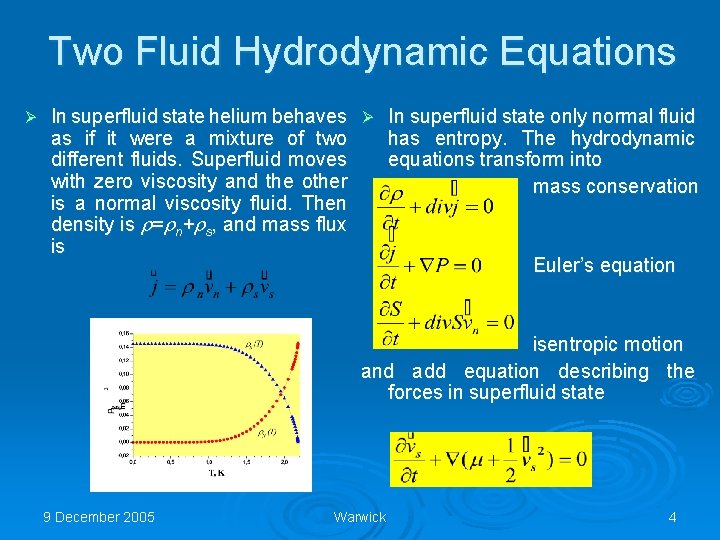
Two Fluid Hydrodynamic Equations Ø In superfluid state helium behaves Ø In superfluid state only normal fluid as if it were a mixture of two has entropy. The hydrodynamic different fluids. Superfluid moves equations transform into with zero viscosity and the other mass conservation is a normal viscosity fluid. Then density is = n+ s, and mass flux is Euler’s equation isentropic motion and add equation describing the forces in superfluid state 9 December 2005 Warwick 4

Sounds in Superfluid Helium The differentiation of two equations with respect to time and substituting into another relationships we obtain for small disturbance (linear waves) Solutions are Ø wave of density (co-moving motion normal and superfluid component) Ø waves of temperature or entropy (countermovement motion normal and superfluid components, = n+ s=const 9 December 2005 Warwick 5

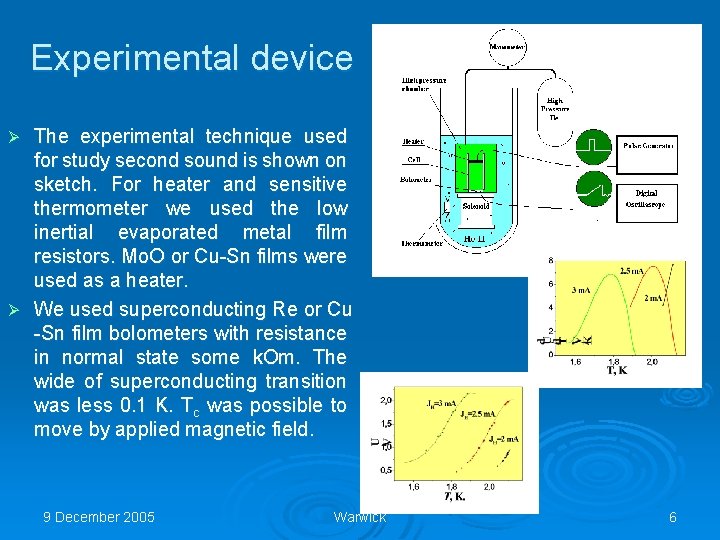
Experimental device The experimental technique used for study second sound is shown on sketch. For heater and sensitive thermometer we used the low inertial evaporated metal film resistors. Mo. O or Cu-Sn films were used as a heater. Ø We used superconducting Re or Cu -Sn film bolometers with resistance in normal state some k. Om. The wide of superconducting transition was less 0. 1 K. Tc was possible to move by applied magnetic field. Ø 9 December 2005 Warwick 6

Ø Ø 9 December 2005 The time resolution of heat pulses by heater and bolometer was better 0. 3 s. The sensitivity of registration pulse by temperature was less 10 -6 K and defined by noise levels. The high pressure chamber allowed us to study the processes of generation of second and first sound waves at different pressures as well as pressure dependence of nonlinear effects. We used cylinder wave guide diameter 15 -30 mm for experiments with second sound wave resonator, L=15 -70 mm. Glass tube with diameter 3 mm with moving heater insert inside the tube was used in experiments with shock waves propagation. Small sizes of the heater allowed us to reach the extremely high intensity of heat pulses. The power density in these experiments was up to 250 W/cm 2 Warwick 7

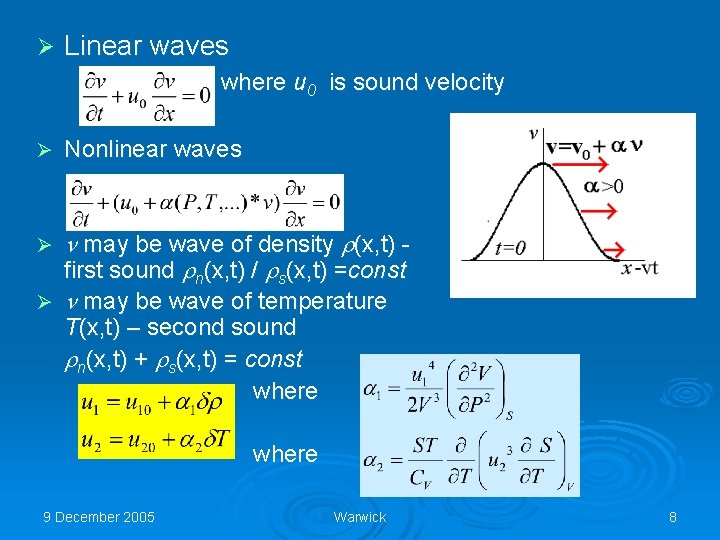
Ø Linear waves where u 0 is sound velocity Ø Nonlinear waves Ø may be wave of density (x, t) first sound n(x, t) / s(x, t) =const may be wave of temperature Ø T(x, t) – second sound n(x, t) + s(x, t) = const where 9 December 2005 Warwick 8

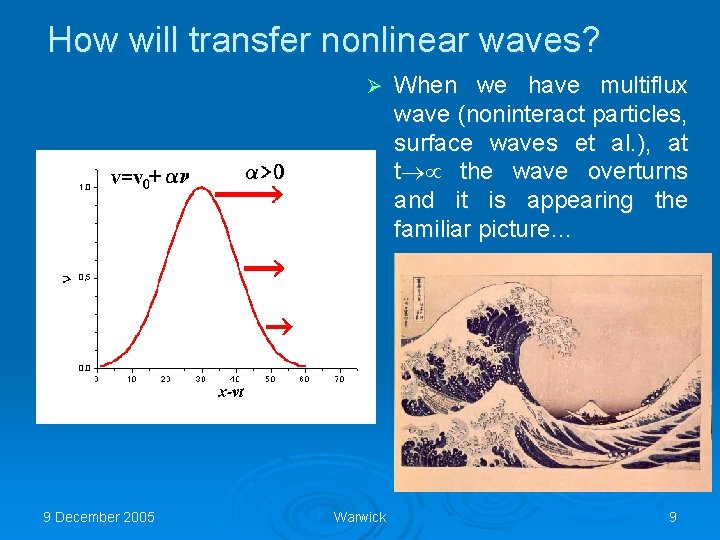
How will transfer nonlinear waves? Ø 9 December 2005 Warwick When we have multiflux wave (noninteract particles, surface waves et al. ), at t®µ the wave overturns and it is appearing the familiar picture… 9

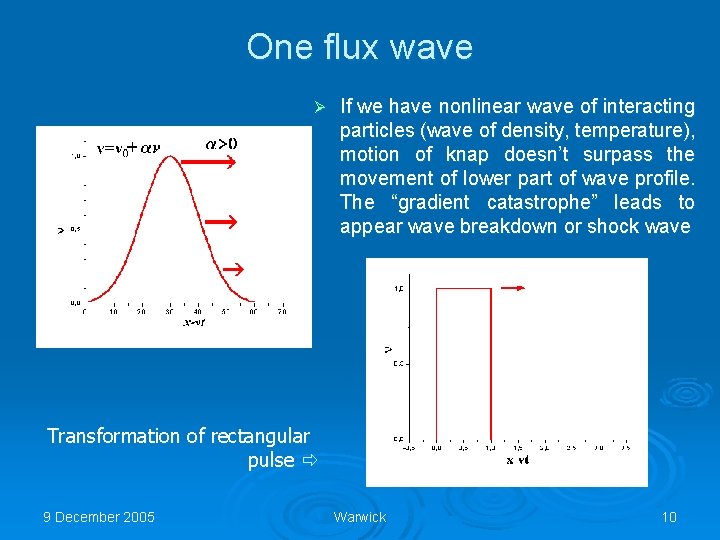
One flux wave Ø If we have nonlinear wave of interacting particles (wave of density, temperature), motion of knap doesn’t surpass the movement of lower part of wave profile. The “gradient catastrophe” leads to appear wave breakdown or shock wave Transformation of rectangular pulse ð 9 December 2005 Warwick 10

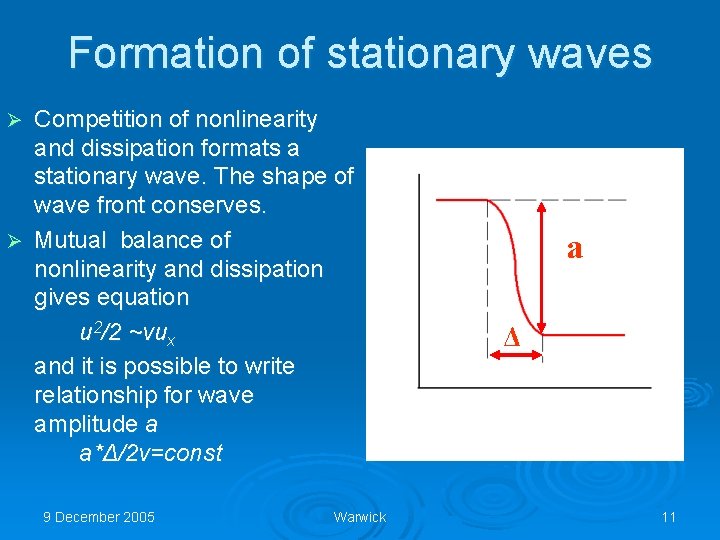
Formation of stationary waves Competition of nonlinearity and dissipation formats a stationary wave. The shape of wave front conserves. Ø Mutual balance of nonlinearity and dissipation gives equation u 2/2 ~νux and it is possible to write relationship for wave amplitude a a*Δ/2ν=const Ø 9 December 2005 Warwick a Δ 11

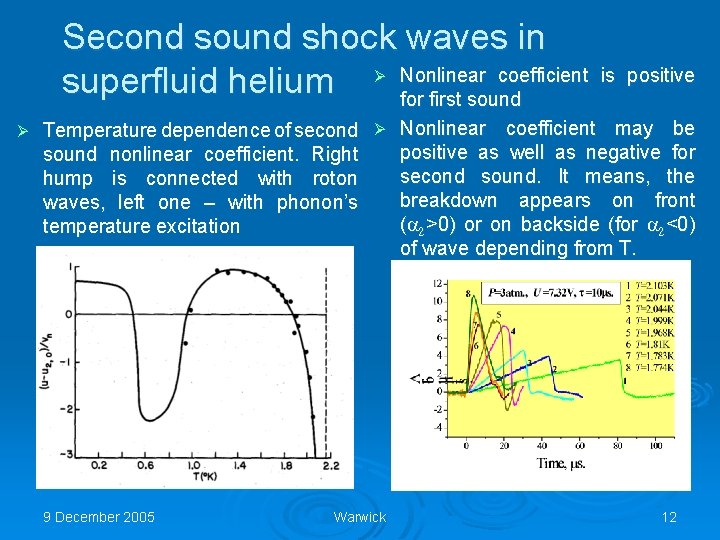
Second sound shock waves in coefficient superfluid helium Ø Nonlinear for first sound Ø is positive Temperature dependence of second Ø Nonlinear coefficient may be positive as well as negative for sound nonlinear coefficient. Right second sound. It means, the hump is connected with roton breakdown appears on front waves, left one – with phonon’s ( 2>0) or on backside (for 2<0) temperature excitation of wave depending from T. 9 December 2005 Warwick 12

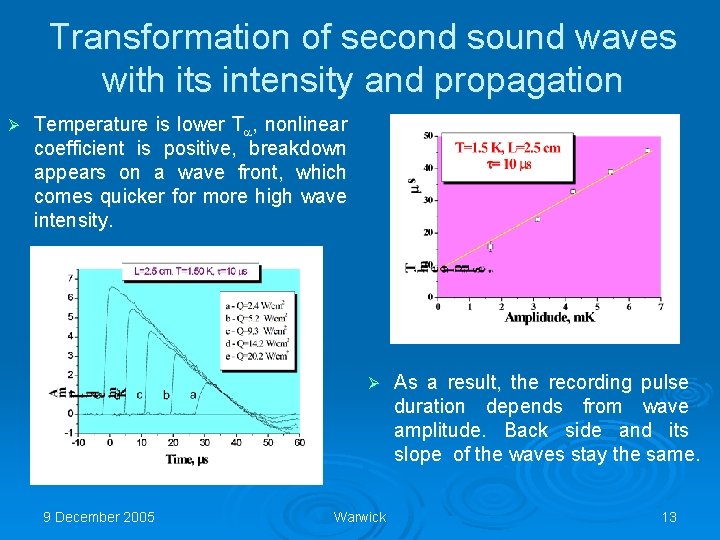
Transformation of second sound waves with its intensity and propagation Ø Temperature is lower T , nonlinear coefficient is positive, breakdown appears on a wave front, which comes quicker for more high wave intensity. Ø 9 December 2005 Warwick As a result, the recording pulse duration depends from wave amplitude. Back side and its slope of the waves stay the same. 13

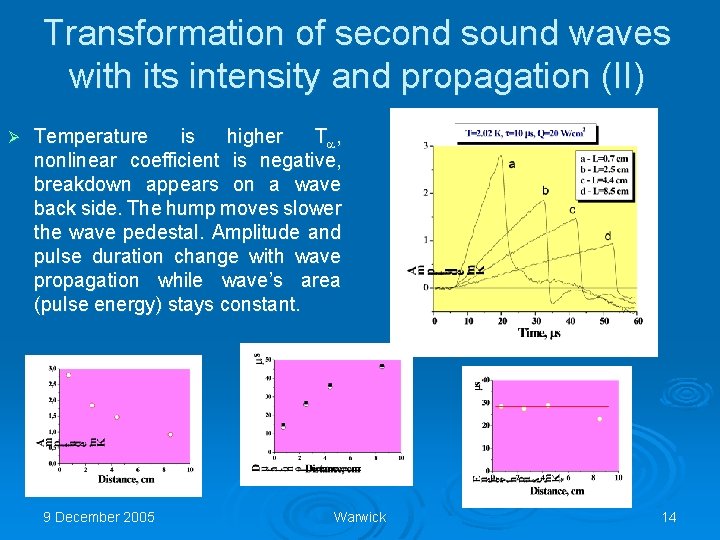
Transformation of second sound waves with its intensity and propagation (II) Ø Temperature is higher T , nonlinear coefficient is negative, breakdown appears on a wave back side. The hump moves slower the wave pedestal. Amplitude and pulse duration change with wave propagation while wave’s area (pulse energy) stays constant. 9 December 2005 Warwick 14

3 -D geometry pulse propagation 9 December 2005 Warwick 15

Wave propagation in 3 -dimensional Ø The first term is outgoing wave, propagated from the origin. The geometry second term is a wave coming to the Ø Spherical or 3 -Dimensional waves centre. A spherical wave has an have dependence density, velocity, amplitude which decreases inversely temperature, pressure only on the as a distance from the centre. The distance from some point. intensity in the wave falls as the square of the distance. And the total Ø The general solution of the wave energy flux in the wave is distributed equation will be determined by equation for velocity potential: Δφ- over a surface whose area (1/c 2) 2φ/ t 2=0. In spherical co- increases as r 2. ordinates the Laplacian transforms Ø A monochromatic stationary the equation into spherical wave is of the form where k= /c We seek a solution in the form φ=f(r, t)/r. Substitution gives us the Ø An outgoing monochromatic ordinary one-dimensional, and spherical wave is given by general solution of the spherical and φ=0 before and equation is after passage of wave. 9 December 2005 Warwick 16

Second Sound Wave Ø in 3 -D geometry Ø The solution of this system is The linearized equation of motion for the second sound can be derived where the ‘retarded’ time ‘t is from general equations of two-fluids introduced ‘t=t-(r-a)/u 20 hydrodynamics. We can introduce a Ø The variation of temperature in the wave potential (r, t) by the relation wave T=- / t and if we integrate p/S= , where p is a momentum of T over all time at any r, the result a unit mass of a helium. The physical is zero quantities can be expressed via the potential by the following way Ø The variation of pressure in the first sound wave P=- / t gives the similar result Then wave equation is rewritten as and boundary condition as q=TSvn, or Ø This means that, the both waves where q is function of of condensation and rarefaction time and a – radius of must be observed in spherical heater. geometry. 9 December 2005 Warwick 17

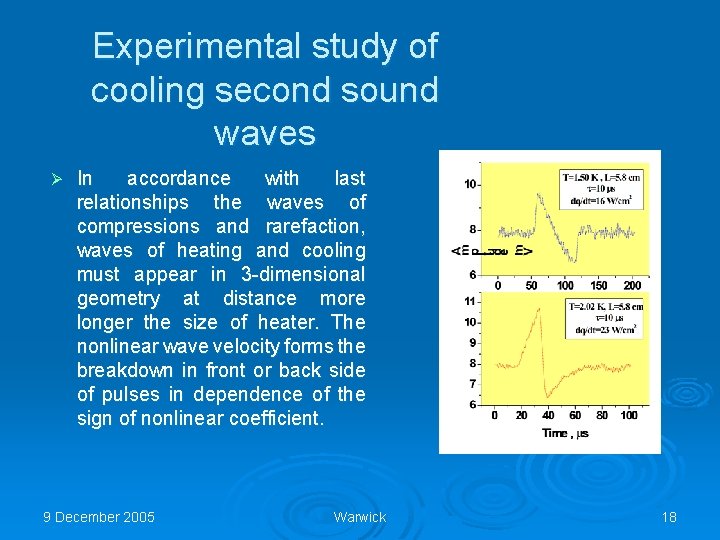
Experimental study of cooling second sound waves Ø In accordance with last relationships the waves of compressions and rarefaction, waves of heating and cooling must appear in 3 -dimensional geometry at distance more longer the size of heater. The nonlinear wave velocity forms the breakdown in front or back side of pulses in dependence of the sign of nonlinear coefficient. 9 December 2005 Warwick 18

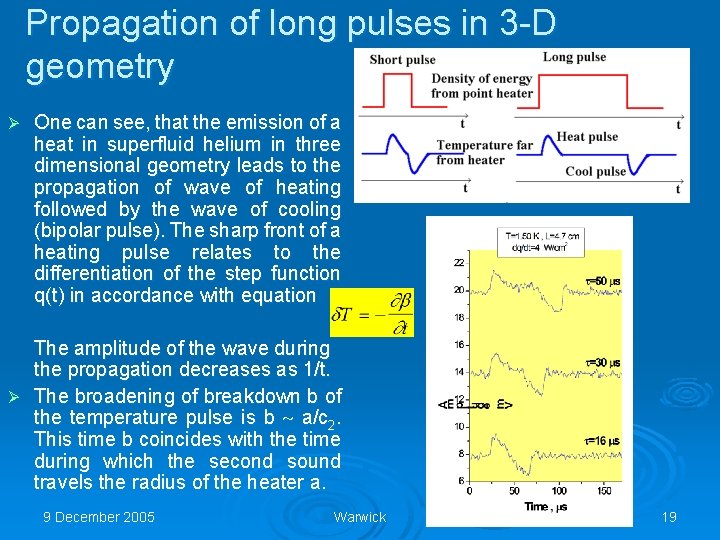
Propagation of long pulses in 3 -D geometry Ø One can see, that the emission of a heat in superfluid helium in three dimensional geometry leads to the propagation of wave of heating followed by the wave of cooling (bipolar pulse). The sharp front of a heating pulse relates to the differentiation of the step function q(t) in accordance with equation The amplitude of the wave during the propagation decreases as 1/t. Ø The broadening of breakdown b of the temperature pulse is b a/c 2. This time b coincides with the time during which the second sound travels the radius of the heater a. 9 December 2005 Warwick 19

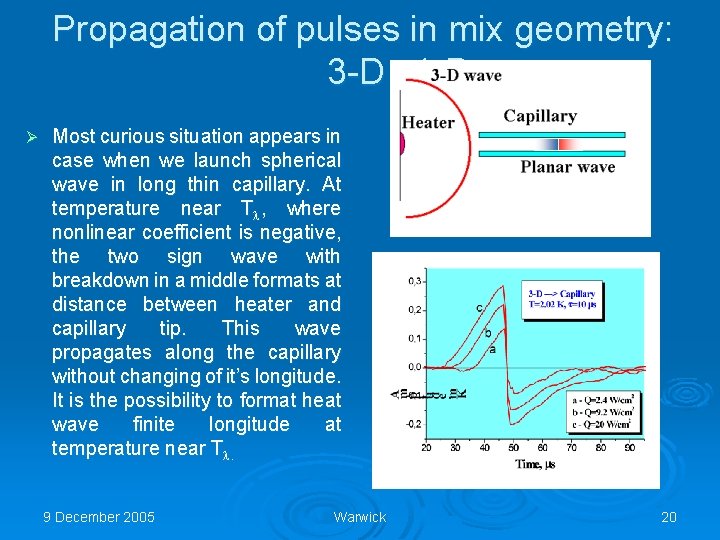
Propagation of pulses in mix geometry: 3 -D ð 1 -D Ø Most curious situation appears in case when we launch spherical wave in long thin capillary. At temperature near T , where nonlinear coefficient is negative, the two sign wave with breakdown in a middle formats at distance between heater and capillary tip. This wave propagates along the capillary without changing of it’s longitude. It is the possibility to format heat wave finite longitude at temperature near T. 9 December 2005 Warwick 20

Stationary nonlinear second sound waves. Energy transformation in Superfluid Helium-4 9 December 2005 Warwick 21

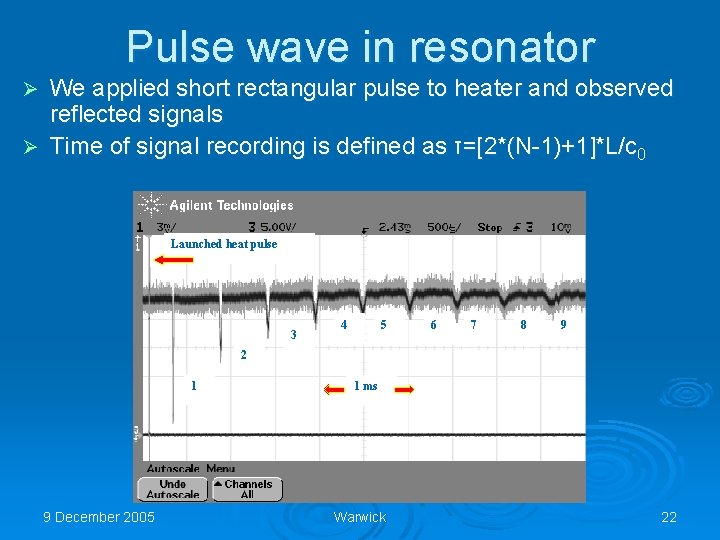
Pulse wave in resonator We applied short rectangular pulse to heater and observed reflected signals Ø Time of signal recording is defined as τ=[2*(N-1)+1]*L/c 0 Ø Launched heat pulse 3 4 5 6 7 8 9 2 1 9 December 2005 1 ms Warwick 22

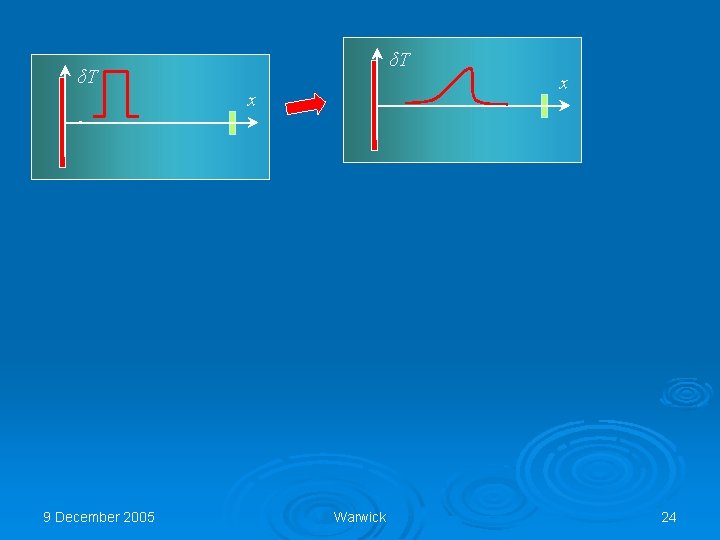
δT 9 December 2005 x Warwick 23

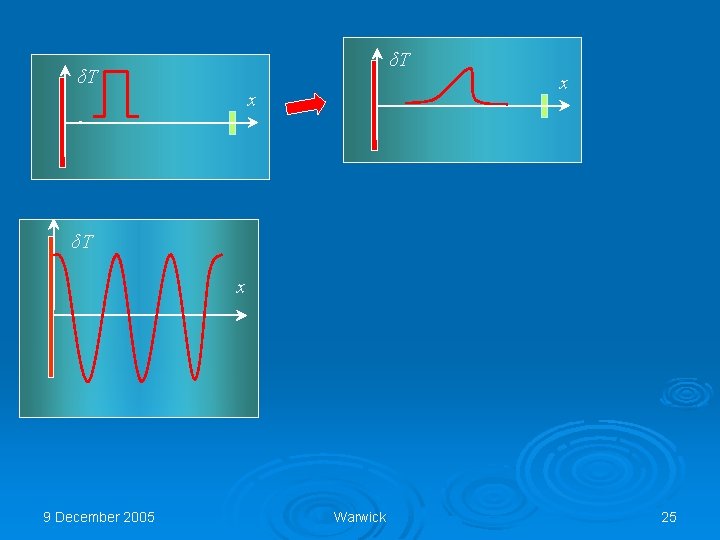
δT 9 December 2005 δT x Warwick x 24

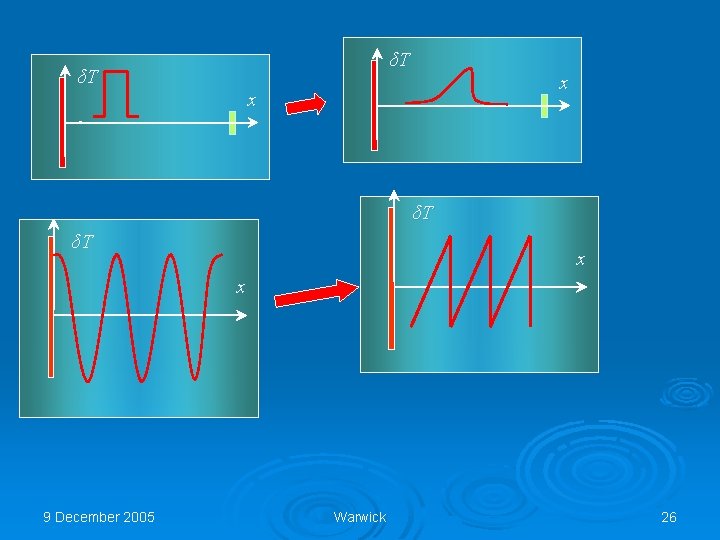
δT δT x x δT x 9 December 2005 Warwick 25

δT δT x x 9 December 2005 Warwick 26

δT δT x δT ? x 9 December 2005 x Warwick 27

δT δT x δT ? x 9 December 2005 x Warwick 28

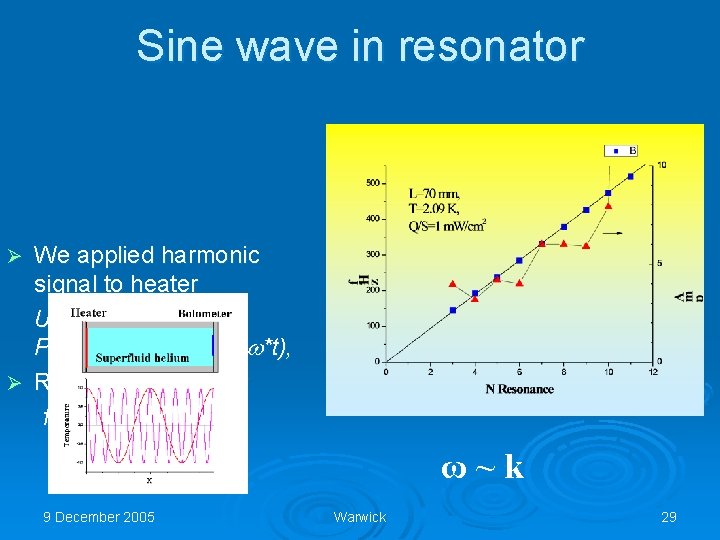
Sine wave in resonator We applied harmonic signal to heater U~sin( *t), P~sin 2( *t)=1+sin(2 *t), Ø Resonant frequency f. G=c 0/4 L Ø ω~k 9 December 2005 Warwick 29

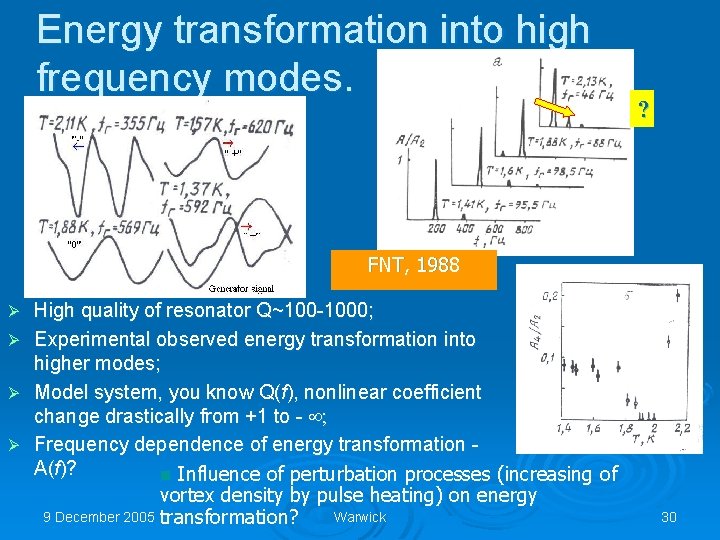
Energy transformation into high frequency modes. ? FNT, 1988 Ø Ø High quality of resonator Q~100 -1000; Experimental observed energy transformation into higher modes; Model system, you know Q(f), nonlinear coefficient change drastically from +1 to - ¥; Frequency dependence of energy transformation A(f)? n Influence of perturbation processes (increasing of vortex density by pulse heating) on energy 9 December 2005 transformation? Warwick 30

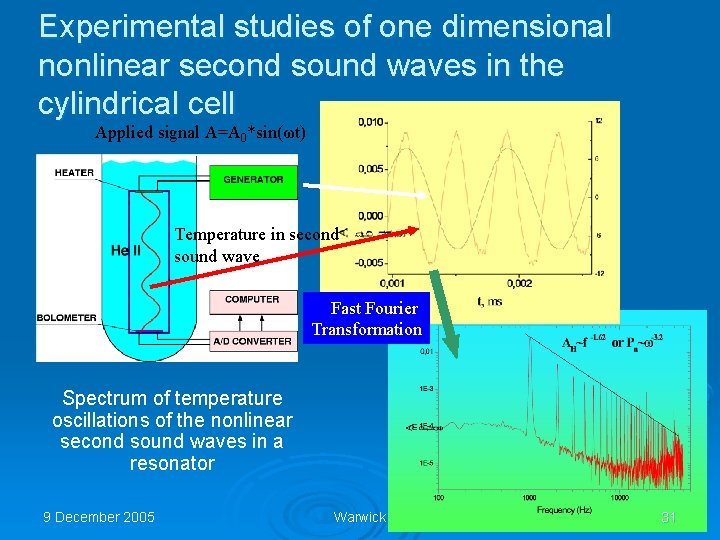
Experimental studies of one dimensional nonlinear second sound waves in the cylindrical cell Applied signal A=A 0*sin(ωt) Temperature in second sound wave Fast Fourier Transformation Spectrum of temperature oscillations of the nonlinear second sound waves in a resonator 9 December 2005 Warwick 31

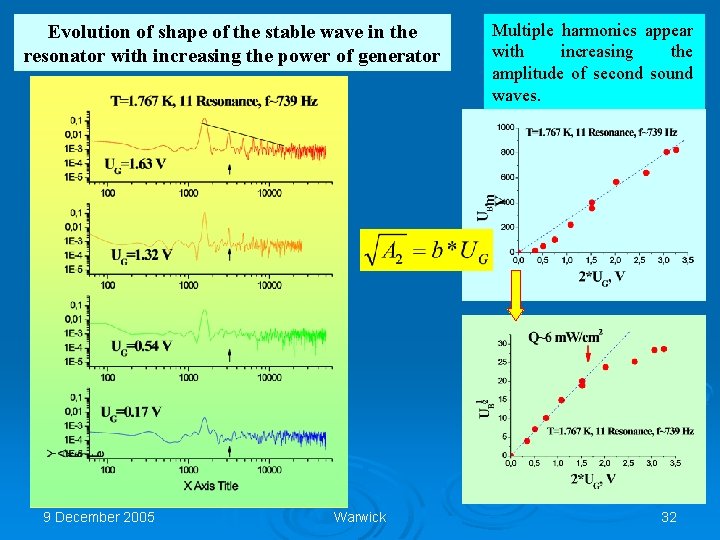
Evolution of shape of the stable wave in the resonator with increasing the power of generator 9 December 2005 Warwick Multiple harmonics appear with increasing the amplitude of second sound waves. 32

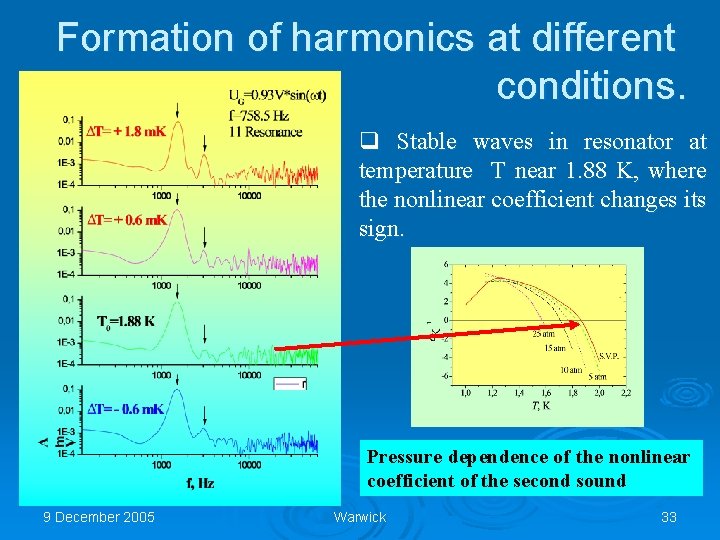
Formation of harmonics at different conditions. q Stable waves in resonator at temperature T near 1. 88 K, where the nonlinear coefficient changes its sign. Pressure dependence of the nonlinear coefficient of the second sound 9 December 2005 Warwick 33

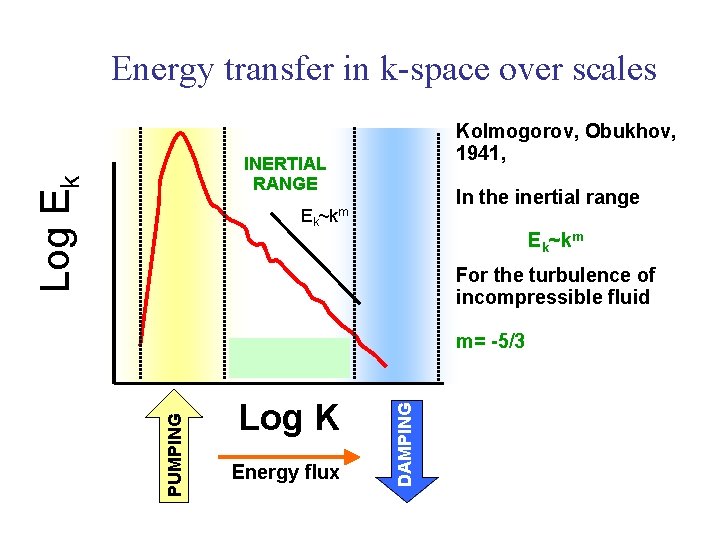
Energy transfer in k-space over scales Kolmogorov, Obukhov, 1941, Log Ek INERTIAL RANGE In the inertial range Ek~km For the turbulence of incompressible fluid Log K Energy flux DAMPING PUMPING m= -5/3

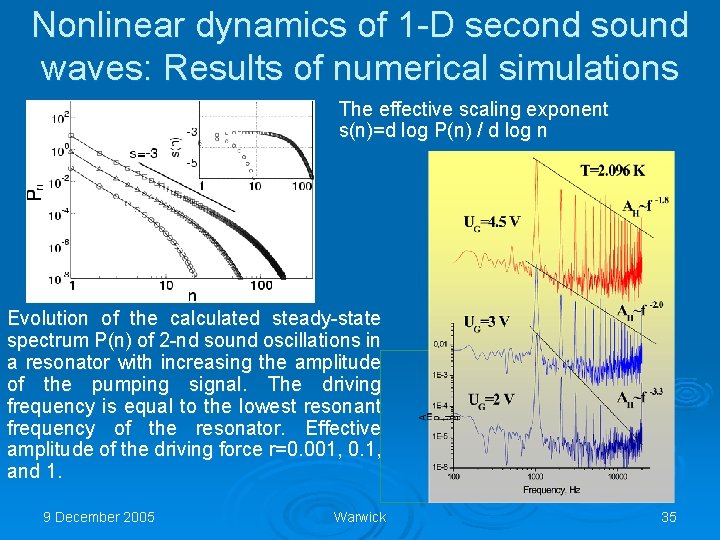
Nonlinear dynamics of 1 -D second sound waves: Results of numerical simulations The effective scaling exponent s(n)=d log P(n) / d log n Evolution of the calculated steady-state spectrum P(n) of 2 -nd sound oscillations in a resonator with increasing the amplitude of the pumping signal. The driving frequency is equal to the lowest resonant frequency of the resonator. Effective amplitude of the driving force r=0. 001, 0. 1, and 1. 9 December 2005 Warwick 35

CONCLUSIONS Experiments with the waves in the bulk of superfluid helium present a unique possibility to study nonlinear and turbulent behaviour in a system of interacting waves. q At high amplitudes of the driving force (or high quality of resonator) a sine second sound wave transforms into periodic one with many multiple harmonics. At high frequencies the power-like spectrum is violated due to transition from the nonlinear wave regime of the energy transfer to the viscous damping. q Experimental studies of turbulence of the 2 -nd sound waves showed the dependence of power-like spectrum from the value of the nonlinear coefficient and amplitude of second sound waves. q 9 December 2005 Warwick 36

Nonstationary energy transformation in resonator. Formation and decay spectrum. 9 December 2005 Warwick 37

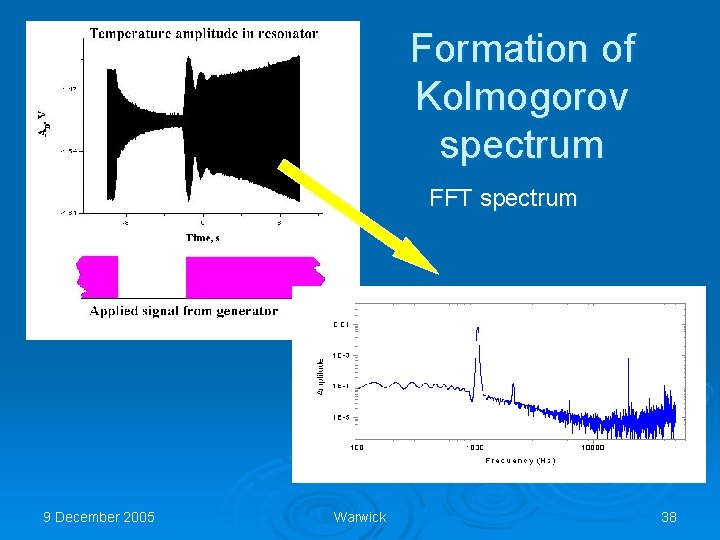
Formation of Kolmogorov spectrum FFT spectrum 9 December 2005 Warwick 38

9 December 2005 Warwick 39

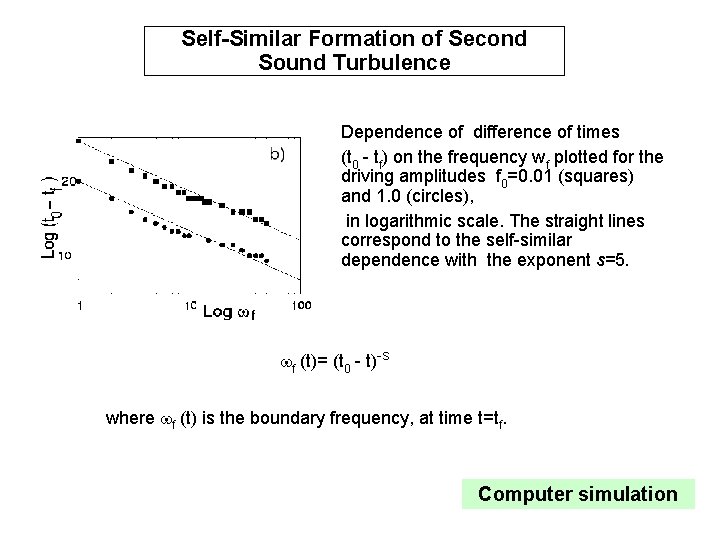
Self-Similar Formation of Second Sound Turbulence Dependence of difference of times (t 0 - tf) on the frequency wf plotted for the driving amplitudes f 0=0. 01 (squares) and 1. 0 (circles), in logarithmic scale. The straight lines correspond to the self-similar dependence with the exponent s=5. wf (t)= (t 0 - t)-s where wf (t) is the boundary frequency, at time t=tf. Computer simulation

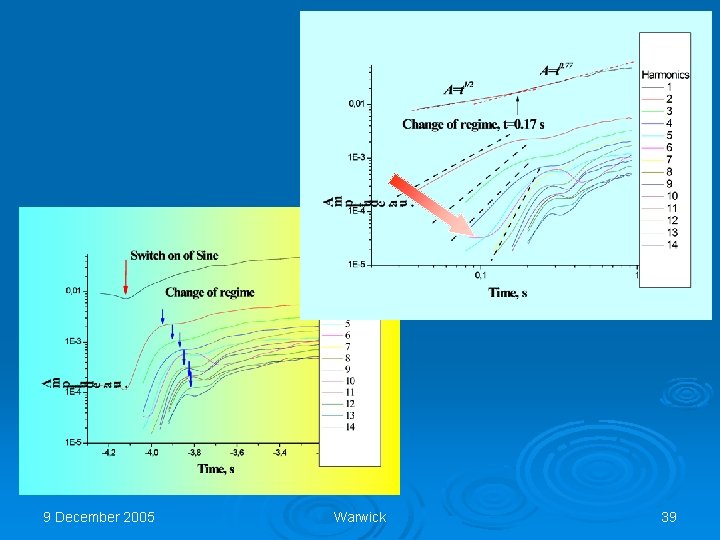
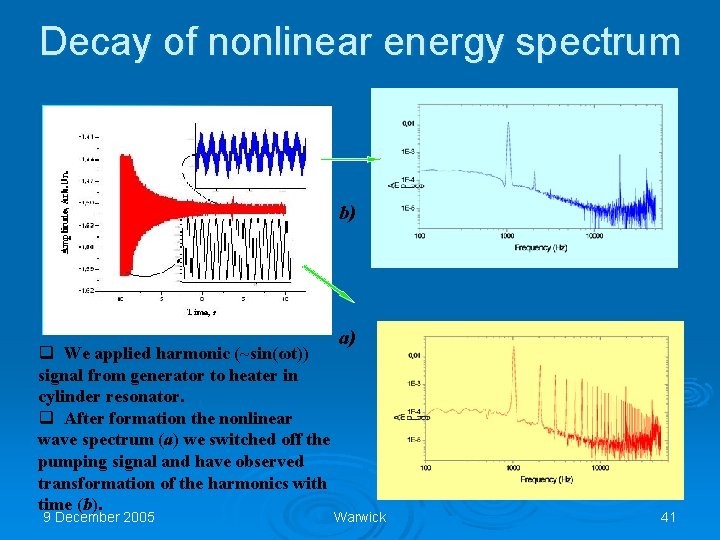
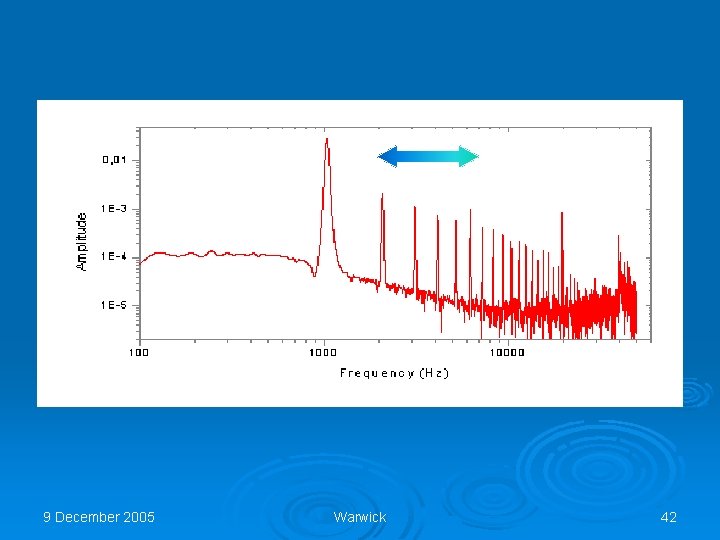
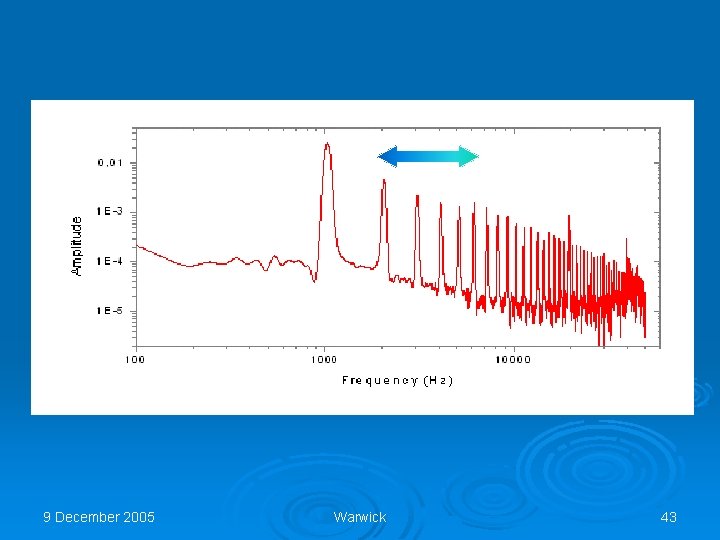
Decay of nonlinear energy spectrum b) q We applied harmonic (~sin(ωt)) signal from generator to heater in cylinder resonator. q After formation the nonlinear wave spectrum (a) we switched off the pumping signal and have observed transformation of the harmonics with time (b). 9 December 2005 a) Warwick 41

9 December 2005 Warwick 42

9 December 2005 Warwick 43

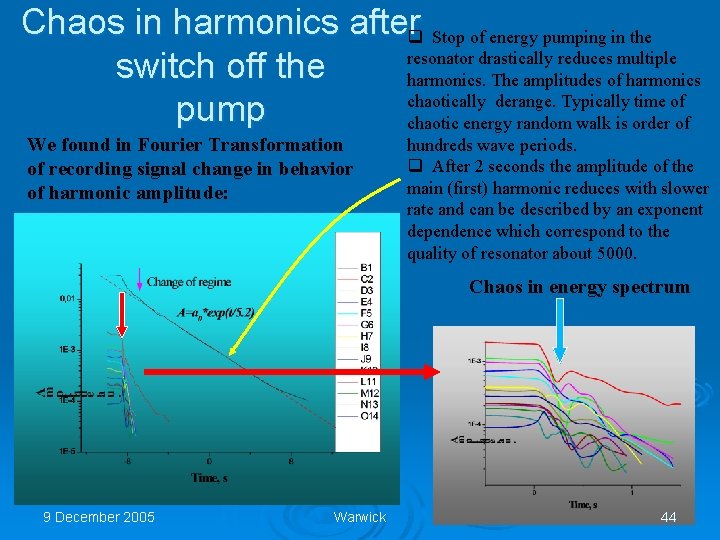
Chaos in harmonics afterq Stop of energy pumping in the resonator drastically reduces multiple switch off the harmonics. The amplitudes of harmonics chaotically derange. Typically time of pump chaotic energy random walk is order of We found in Fourier Transformation of recording signal change in behavior of harmonic amplitude: hundreds wave periods. q After 2 seconds the amplitude of the main (first) harmonic reduces with slower rate and can be described by an exponent dependence which correspond to the quality of resonator about 5000. Chaos in energy spectrum 9 December 2005 Warwick 44

Conclusions The equation of nonlinear second sound wave in resonator utt- (с0 +α u )2 uxx=-ν uxxx at 0<x<L utt- (с0 +α u )2 uxx=-ν uxxx + F(t) at x=0, where F(t)=A*sin (w*t) or =0 ux=0 at x=0, x=L Ø Formation of kolmogorov spectrum – energy transformation from low to high frequencies. Ø Decay of nonlinear harmonic spectrum can be explained by chaotic energy transformation. Ø 9 December 2005 Warwick 45

Disturbance in superfluid helium. Ø Ø 9 December 2005 Measurements in 3 -D geometry; Long pulse; Bipolar pulse (pulse of heating, undisturbed medium – normal and superfluid components counter-flow, pulse of cooling) forms in helium at distance >> size of heater; Intensive heat pulse counter-flow increases the vortex tangle and relaxation in medium, second pulse significant decreases Warwick 46

Conclusions Ø The superfluid helium is perfect model medium for study nonlinear effects, energy transformation and interaction of waves of different nature – wave of first and second sounds. 9 December 2005 Warwick 47

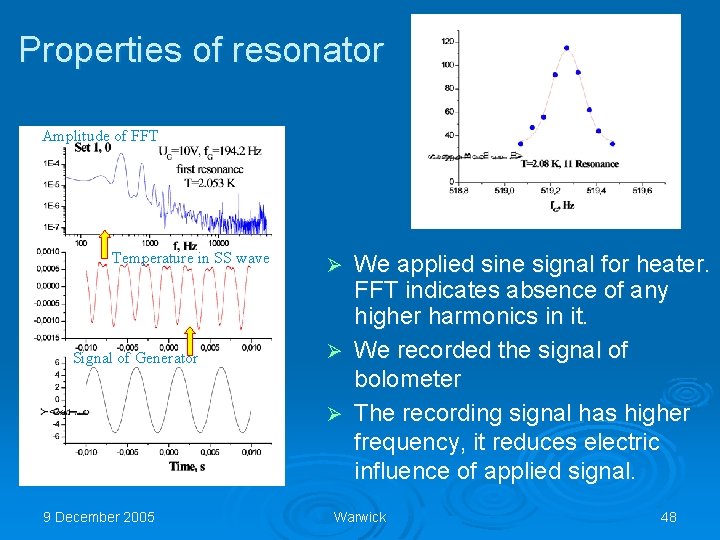
Properties of resonator Amplitude of FFT Temperature in SS wave Signal of Generator 9 December 2005 We applied sine signal for heater. FFT indicates absence of any higher harmonics in it. Ø We recorded the signal of bolometer Ø The recording signal has higher frequency, it reduces electric influence of applied signal. Ø Warwick 48

One direction waves Wave equations Linear wave ut+c 0 ux=0 nonlinearity dissipation ut+c 0 ux= νuxx ut+(c 0+αu)ux=0 In moving system x’=x-c 0 t ut=0 ut+uux=0 ut= νuxx Two direction waves 9 December 2005 ut+(c 0+αu)ux=νuxx ut+ uux = νuxx utt- с02 uxx=-νuxxx utt- (с0 -α u )2 uxx=0 utt- с20 uxx - (u ux)x=0 Utt-c 02 uxx=0 Nonlinearity and dissipation utt- (с0 -α u )2 uxx=-ν uxxx utt- с20 uxx - (u ux)x =-νuxxx Warwick 49

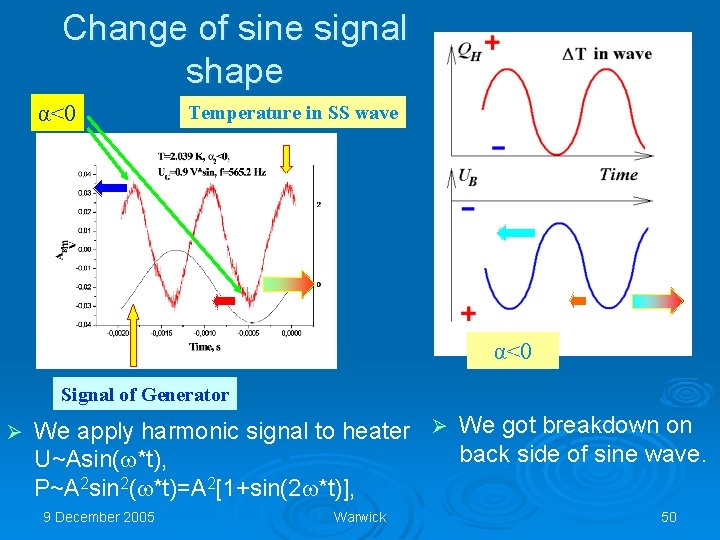
Change of sine signal shape α<0 Temperature in SS wave α<0 Signal of Generator Ø We apply harmonic signal to heater Ø We got breakdown on back side of sine wave. U~Asin(w*t), P~A 2 sin 2(w*t)=A 2[1+sin(2 w*t)], 9 December 2005 Warwick 50