Experimental Skills in Physics B Sc Part I

Experimental Skills in Physics (B. Sc. Part - I) Dr. T. J. SHINDE Department of physics Smt. K. R. P. Kanya Mahavidyalaya, Islampur, Dist. - Sangli-415 409
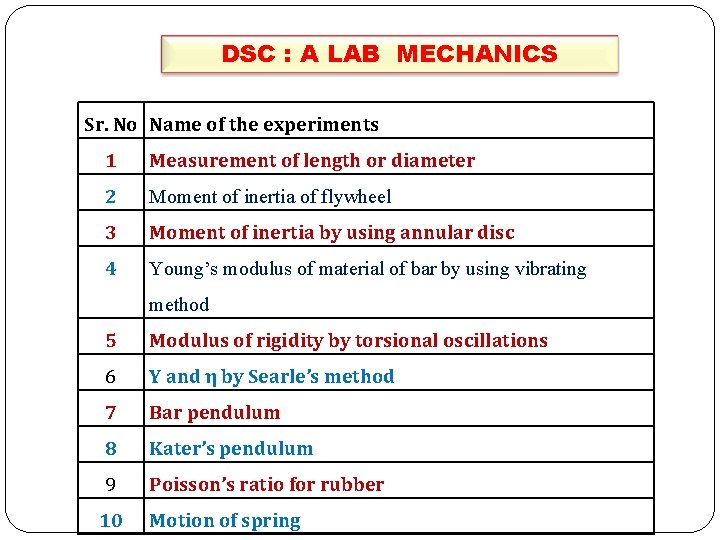
DSC : A LAB MECHANICS Sr. No Name of the experiments 1 Measurement of length or diameter 2 Moment of inertia of flywheel 3 Moment of inertia by using annular disc 4 Young’s modulus of material of bar by using vibrating method 5 Modulus of rigidity by torsional oscillations 6 Y and η by Searle’s method 7 Bar pendulum 8 Kater’s pendulum 9 Poisson’s ratio for rubber 10 Motion of spring
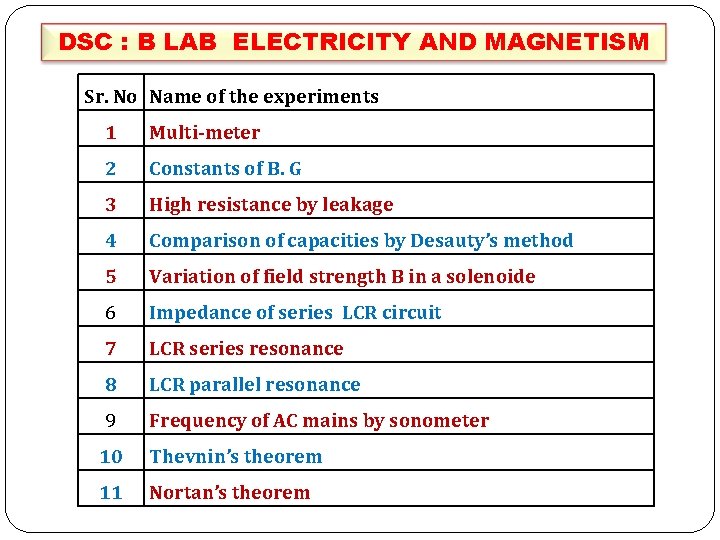
DSC : B LAB ELECTRICITY AND MAGNETISM Sr. No Name of the experiments 1 Multi-meter 2 Constants of B. G 3 High resistance by leakage 4 Comparison of capacities by Desauty’s method 5 Variation of field strength B in a solenoide 6 Impedance of series LCR circuit 7 LCR series resonance 8 LCR parallel resonance 9 Frequency of AC mains by sonometer 10 Thevnin’s theorem 11 Nortan’s theorem
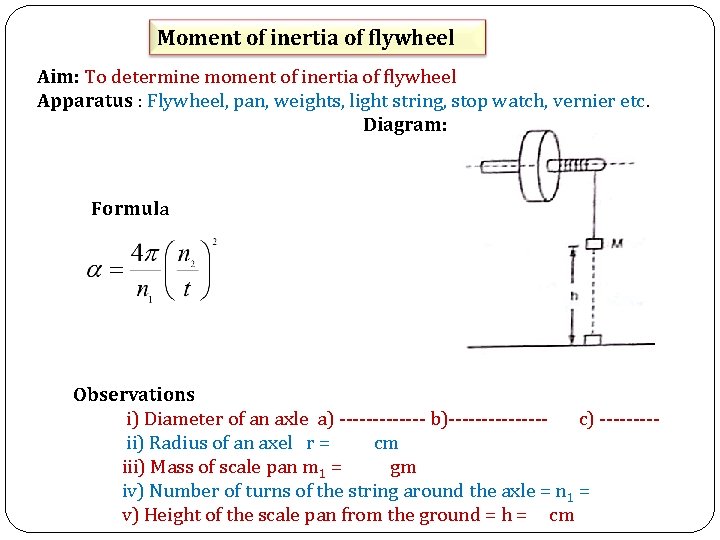
Moment of inertia of flywheel Aim: To determine moment of inertia of flywheel Apparatus : Flywheel, pan, weights, light string, stop watch, vernier etc. Diagram: Formula Observations i) Diameter of an axle a) ------- b)-------c) ----ii) Radius of an axel r = cm iii) Mass of scale pan m 1 = gm iv) Number of turns of the string around the axle = n 1 = v) Height of the scale pan from the ground = h = cm
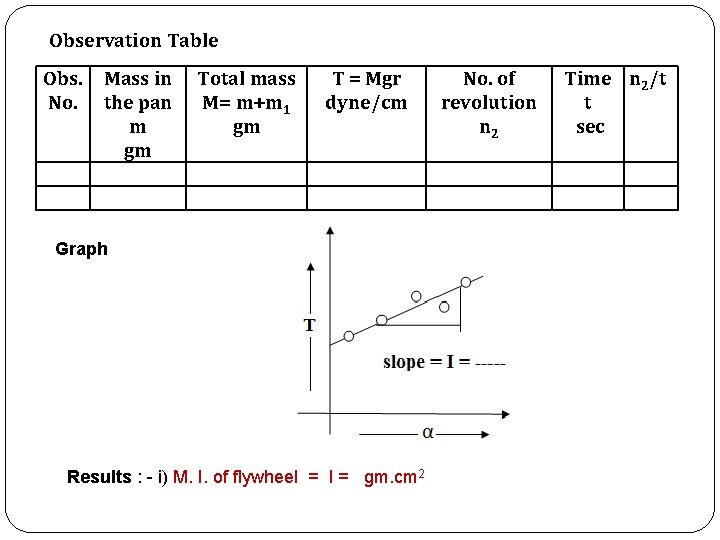
Observation Table Obs. No. Mass in the pan m gm Total mass M= m+m 1 gm T = Mgr dyne/cm Graph Results : - i) M. I. of flywheel = I = gm. cm 2 No. of revolution n 2 Time n 2/t t sec
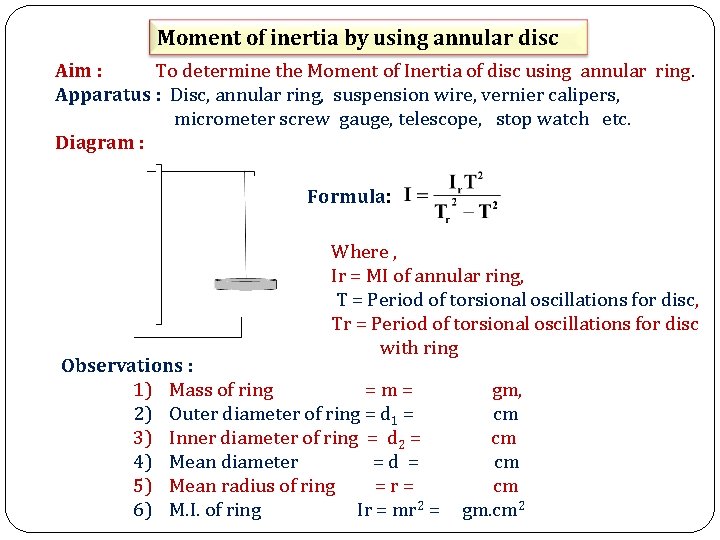
Moment of inertia by using annular disc Aim : To determine the Moment of Inertia of disc using annular ring. Apparatus : Disc, annular ring, suspension wire, vernier calipers, micrometer screw gauge, telescope, stop watch etc. Diagram : Formula: Where , Ir = MI of annular ring, T = Period of torsional oscillations for disc, Tr = Period of torsional oscillations for disc with ring Observations : 1) Mass of ring =m= 2) Outer diameter of ring = d 1 = 3) Inner diameter of ring = d 2 = 4) Mean diameter =d = 5) Mean radius of ring =r= 6) M. I. of ring Ir = mr 2 = gm, cm cm gm. cm 2
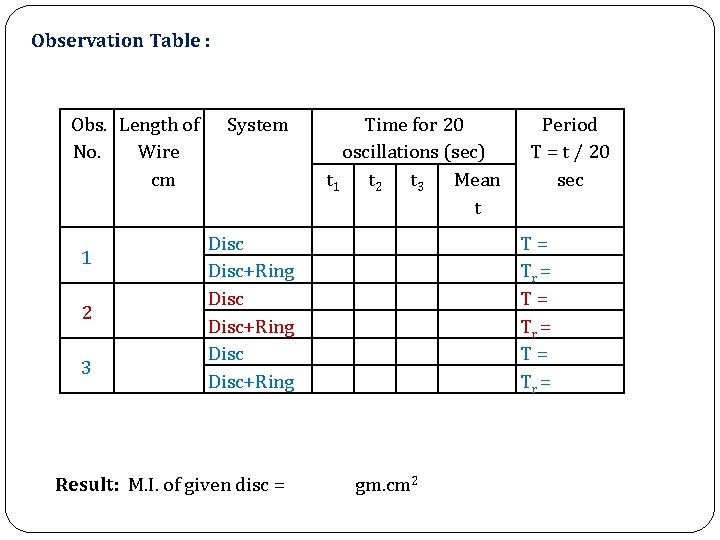
Observation Table : Obs. Length of No. Wire cm 1 2 3 System Time for 20 oscillations (sec) t 1 t 2 t 3 Mean t Disc+Ring Disc+Ring Result: M. I. of given disc = Period T = t / 20 sec T= Tr = gm. cm 2
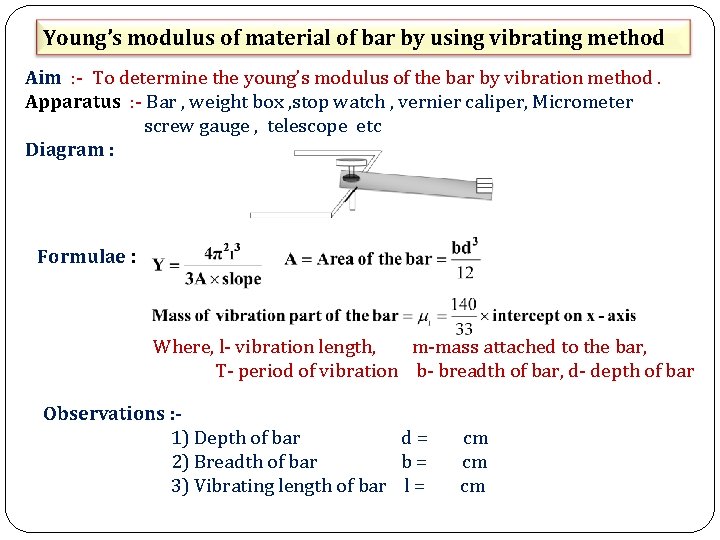
Young’s modulus of material of bar by using vibrating method Aim : - To determine the young’s modulus of the bar by vibration method. Apparatus : - Bar , weight box , stop watch , vernier caliper, Micrometer screw gauge , telescope etc Diagram : Formulae : Where, l- vibration length, m-mass attached to the bar, T- period of vibration b- breadth of bar, d- depth of bar Observations : 1) Depth of bar d= 2) Breadth of bar b= 3) Vibrating length of bar l = cm cm cm
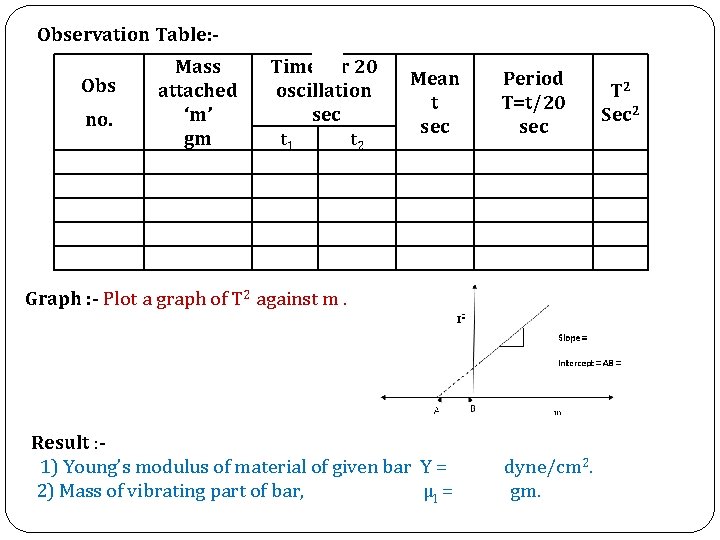
Observation Table: Obs no. Mass attached ‘m’ gm Time for 20 oscillation sec t 1 t 2 Mean t sec Period T=t/20 sec Graph : - Plot a graph of T 2 against m. Result : 1) Young’s modulus of material of given bar Y = 2) Mass of vibrating part of bar, μl = dyne/cm 2. gm. T 2 Sec 2

Modulus of rigidity by torsional oscillations Aim : - Determine the modulus of rigidity of the material of wire by dynamical method using a solid disc. Apparatus : - steel wire , solid disc , stop watch etc. Diagram : Formulae : Where, moment of inertia I = MR 2/2= --gm. cm 2 Observations : - 1) Mass of solid disc M =-----------gm. 2) Diameter of solid disc d = ---------- cm. 3) Radius of solid disc R =---------- cm. 4) Reading for diameter of steel wire. i) ---------iii)-----Mean diameter D = cm. 5) Mean radius wire r= cm.
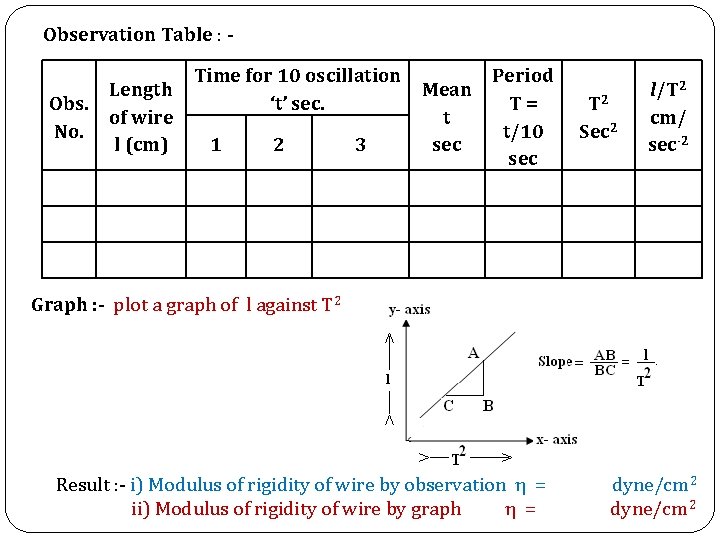
Observation Table : Obs. No. Length of wire l (cm) Time for 10 oscillation ‘t’ sec. 1 2 3 Mean t sec Period T= t/10 sec T 2 Sec 2 l/T 2 cm/ sec-2 Graph : - plot a graph of l against T 2 Result : - i) Modulus of rigidity of wire by observation η = ii) Modulus of rigidity of wire by graph η = dyne/cm 2

Y and η by Searle’s method Aim: To determine Young’s modulus and modulus ofthe material of a given wire by Searle’s method. Apparatus: Two identical bar, wire, stop watch, screw gauge, vernier caliper, thread and scale etc. Diagram : - Formulae: Where, = length of given wire between two bar r = radius of wire, b= Breadth of bar T =time period when two bar execute S. H. M together or flexural oscillation,
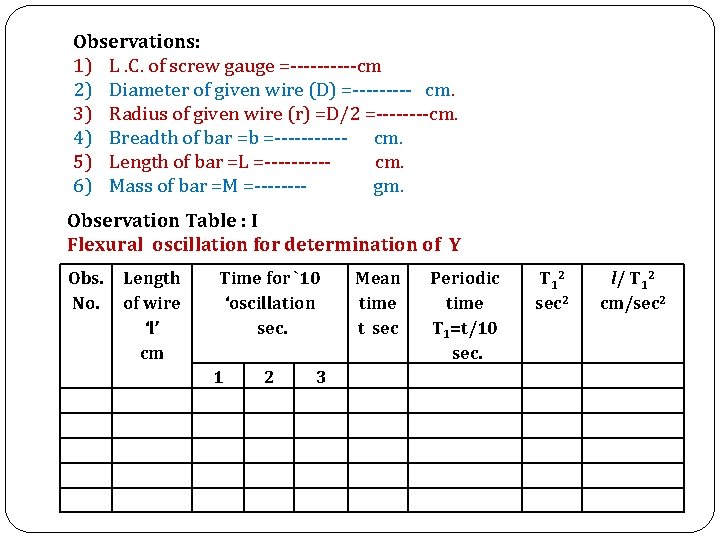
Observations: 1) L. C. of screw gauge =-----cm 2) Diameter of given wire (D) =----- cm. 3) Radius of given wire (r) =D/2 =----cm. 4) Breadth of bar =b =------ cm. 5) Length of bar =L =-----cm. 6) Mass of bar =M =-------gm. Observation Table : I Flexural oscillation for determination of Y Obs. No. Length of wire ‘l’ cm Time for `10 ‘oscillation sec. 1 2 3 Mean time t sec Periodic time T 1=t/10 sec. T 12 sec 2 l/ T 12 cm/sec 2
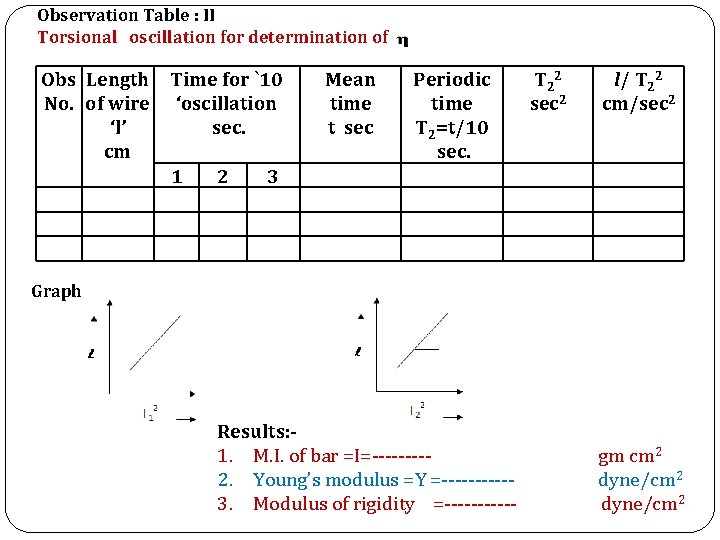
Observation Table : II Torsional oscillation for determination of Obs Length No. of wire ‘l’ cm Time for `10 ‘oscillation sec. 1 2 Mean time t sec Periodic time T 2=t/10 sec. T 2 2 sec 2 l/ T 22 cm/sec 2 3 Graph Results: 1. M. I. of bar =I=----2. Young’s modulus =Y =-----3. Modulus of rigidity =------ gm cm 2 dyne/cm 2
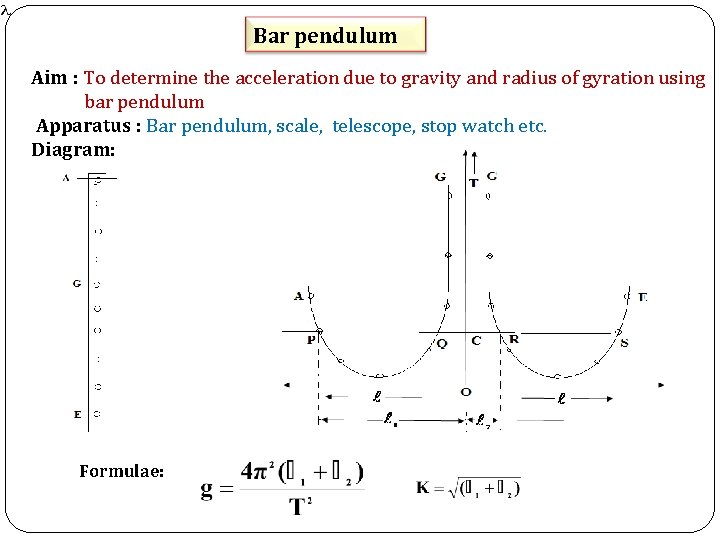
Bar pendulum Aim : To determine the acceleration due to gravity and radius of gyration using bar pendulum Apparatus : Bar pendulum, scale, telescope, stop watch etc. Diagram: Formulae:
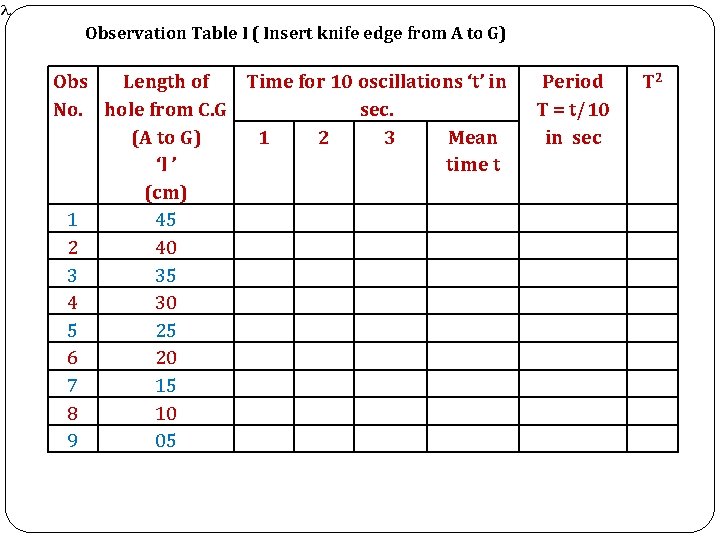
Observation Table I ( Insert knife edge from A to G) Obs Length of Time for 10 oscillations ‘t’ in No. hole from C. G sec. (A to G) 1 2 3 Mean ‘l ’ time t (cm) 1 45 2 40 3 35 4 30 5 25 6 20 7 15 8 10 9 05 Period T = t/10 in sec T 2
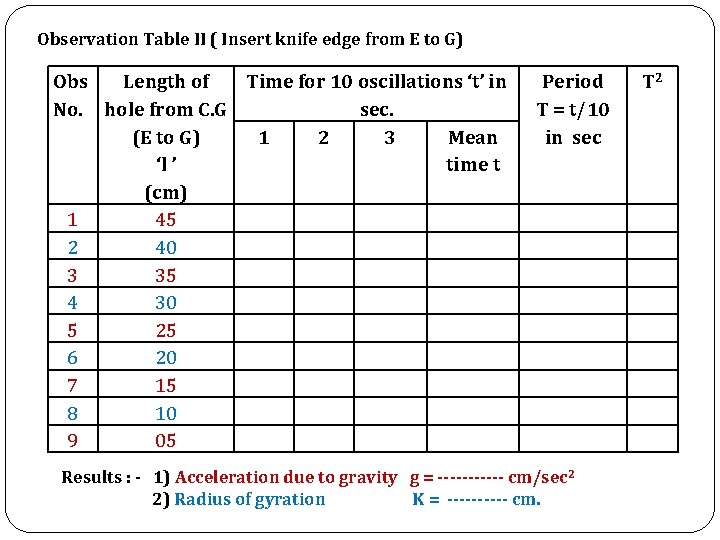
Observation Table II ( Insert knife edge from E to G) Obs Length of Time for 10 oscillations ‘t’ in No. hole from C. G sec. (E to G) 1 2 3 Mean ‘l ’ time t (cm) 1 45 2 40 3 35 4 30 5 25 6 20 7 15 8 10 9 05 Period T = t/10 in sec Results : - 1) Acceleration due to gravity g = ------ cm/sec 2 2) Radius of gyration K = ----- cm. T 2
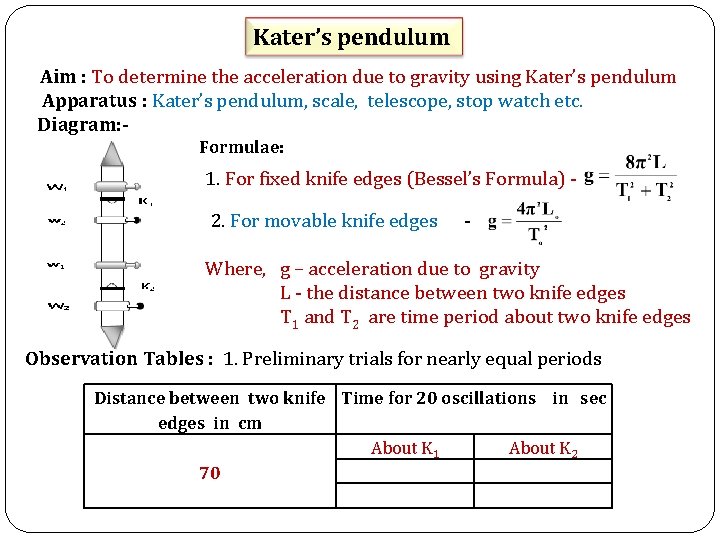
Kater’s pendulum Aim : To determine the acceleration due to gravity using Kater’s pendulum Apparatus : Kater’s pendulum, scale, telescope, stop watch etc. Diagram: Formulae: 1. For fixed knife edges (Bessel’s Formula) 2. For movable knife edges - Where, g – acceleration due to gravity L - the distance between two knife edges T 1 and T 2 are time period about two knife edges Observation Tables : 1. Preliminary trials for nearly equal periods Distance between two knife Time for 20 oscillations in sec edges in cm About K 1 About K 2 70
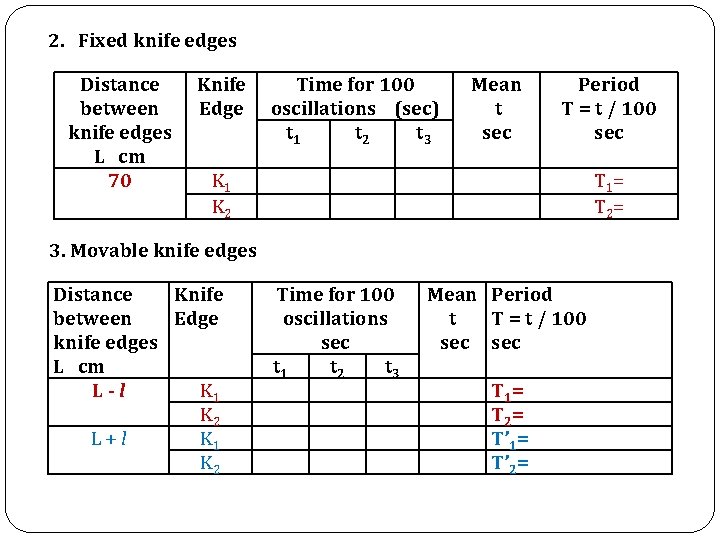
2. Fixed knife edges Distance between knife edges L cm 70 Knife Edge Time for 100 oscillations (sec) t 1 t 2 t 3 Mean t sec Period T = t / 100 sec K 1 K 2 T 1= T 2= 3. Movable knife edges Distance Knife between Edge knife edges L cm L-l K 1 K 2 L+l K 1 K 2 Time for 100 oscillations sec t 1 t 2 t 3 Mean Period t T = t / 100 sec T 1 = T 2 = T’ 1= T’ 2=
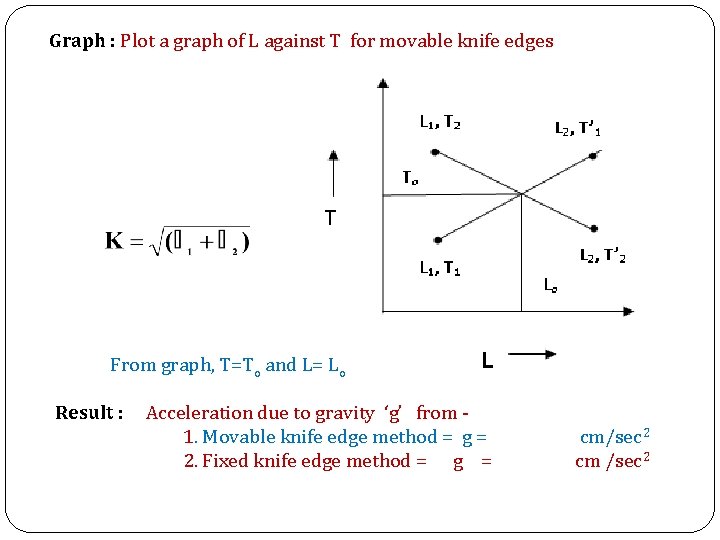
Graph : Plot a graph of L against T for movable knife edges From graph, T=To and L= Lo Result : Acceleration due to gravity ‘g’ from 1. Movable knife edge method = g = 2. Fixed knife edge method = g = cm/sec 2 cm /sec 2
Poisson’s ratio for rubber Aim : To determine the value of Poisson’s ratio for rubber. Apparatus : Rubber tube, slotted weights, specimen tube, vernier, micrometer, burette etc. Diagram Formulae: Observations : 1. Outer diameter of rubber tube D = 2. Outer radius of rubber tube R = 3. Thickness of the sample t= 4 Inner radius of the tube r = R-t = cm cm
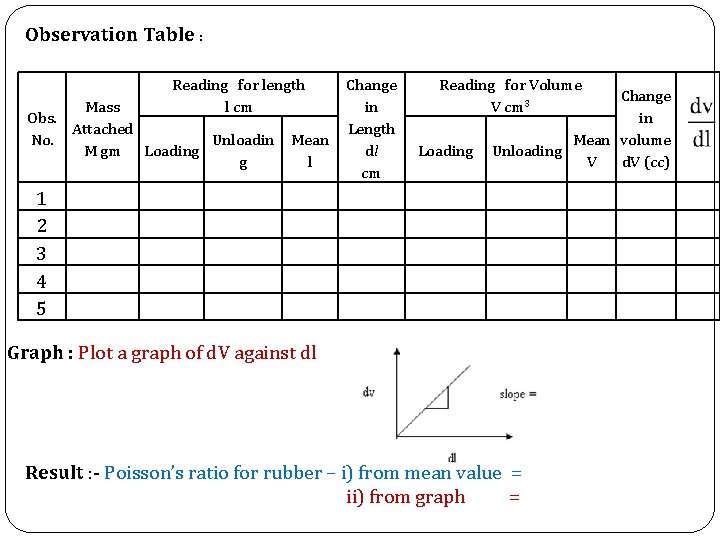
Observation Table : Reading for length l cm Mass Obs. Attached No. Unloadin M gm Loading g Mean l Change in Length dl cm Reading for Volume V cm 3 Loading Change in Mean volume Unloading d. V (cc) V 1 2 3 4 5 Graph : Plot a graph of d. V against dl Result : - Poisson’s ratio for rubber – i) from mean value = ii) from graph =
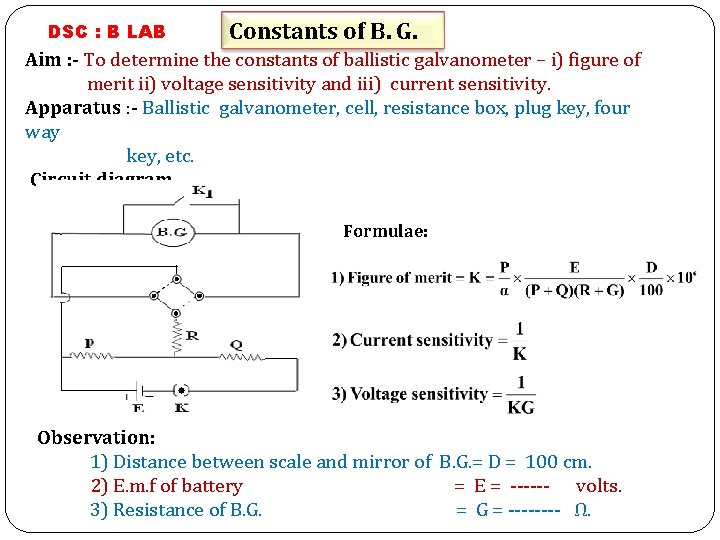
DSC : B LAB Constants of B. G. Aim : - To determine the constants of ballistic galvanometer – i) figure of merit ii) voltage sensitivity and iii) current sensitivity. Apparatus : - Ballistic galvanometer, cell, resistance box, plug key, four way key, etc. Circuit diagram Formulae: Observation: 1) Distance between scale and mirror of B. G. = D = 100 cm. 2) E. m. f of battery = E = ------ volts. 3) Resistance of B. G. = G = ---- Ω.
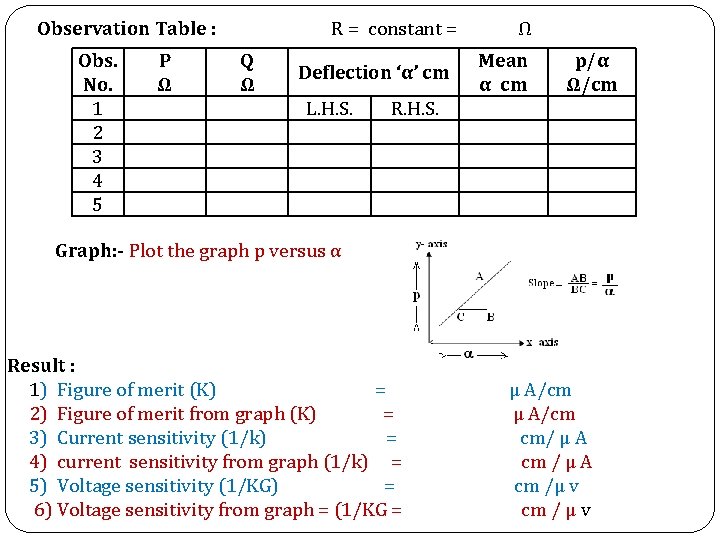
Observation Table : Obs. No. 1 2 3 4 5 P Ω R = constant = Q Ω Deflection ‘α’ cm L. H. S. Ω Mean α cm p/α Ω/cm R. H. S. Graph: - Plot the graph p versus α Result : 1) Figure of merit (K) = 2) Figure of merit from graph (K) = 3) Current sensitivity (1/k) = 4) current sensitivity from graph (1/k) = 5) Voltage sensitivity (1/KG) = 6) Voltage sensitivity from graph = (1/KG = µ A/cm μ A/cm cm/ µ A cm / μ A cm /µ v cm / μ v
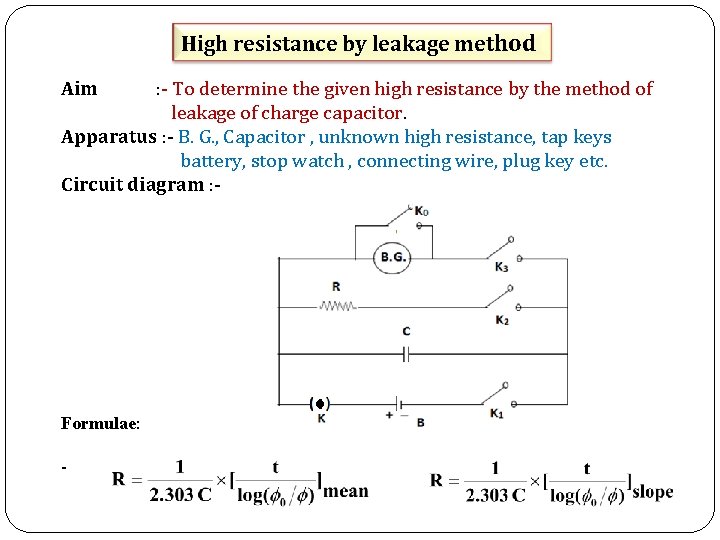
High resistance by leakage method Aim : - To determine the given high resistance by the method of leakage of charge capacitor. Apparatus : - B. G. , Capacitor , unknown high resistance, tap keys battery, stop watch , connecting wire, plug key etc. Circuit diagram : - Formulae: -
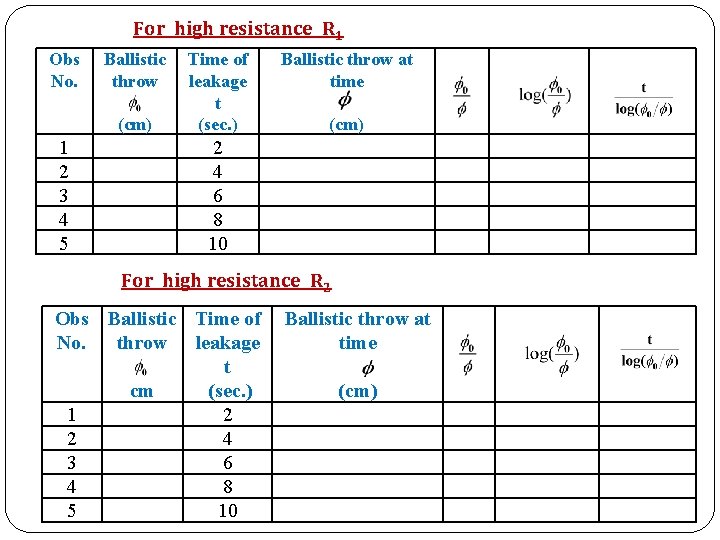
For high resistance R 1 Obs No. Ballistic throw (cm) 1 2 3 4 5 Time of leakage t (sec. ) Ballistic throw at time (cm) 2 4 6 8 10 For high resistance R 2 Obs Ballistic Time of No. throw leakage t cm (sec. ) 1 2 2 4 3 6 4 8 5 10 Ballistic throw at time (cm)
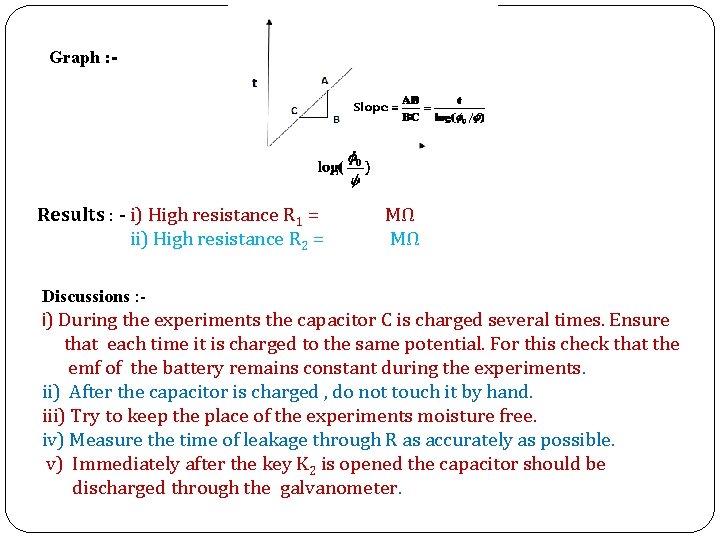
Graph : - Results : - i) High resistance R 1 = ii) High resistance R 2 = MΩ MΩ Discussions : i) During the experiments the capacitor C is charged several times. Ensure that each time it is charged to the same potential. For this check that the emf of the battery remains constant during the experiments. ii) After the capacitor is charged , do not touch it by hand. iii) Try to keep the place of the experiments moisture free. iv) Measure the time of leakage through R as accurately as possible. v) Immediately after the key K 2 is opened the capacitor should be discharged through the galvanometer.

Comparison of capacities by Desauty’s method Aim : - To determine the ratio’s of the capacities CA: CB & CA: CC of condensers A, B, C if CA=------µF (given). Find CB and CC by De Sauty’s method. Apparatus : - Capacitors, resistance boxes, B. G. , battery, De Sauty’s key etc. . Circuit diagram : - Formula: i) CA/CB = R 2/R 1 Observation: - Given, ii). CA/CC = R 2/R 1 CA =……. . F.
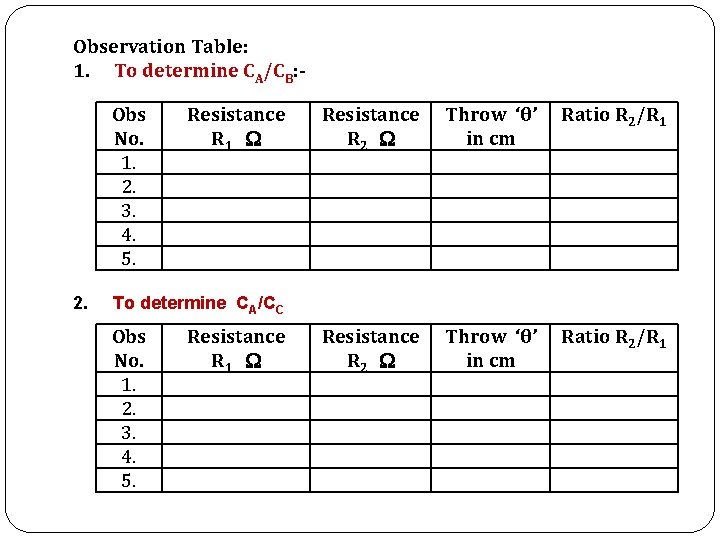
Observation Table: 1. To determine CA/CB: Obs No. 1. 2. 3. 4. 5. 2. Resistance R 1 Resistance R 2 Throw ‘θ’ in cm Ratio R 2/R 1 To determine CA/CC Obs No. 1. 2. 3. 4. 5. Resistance R 1
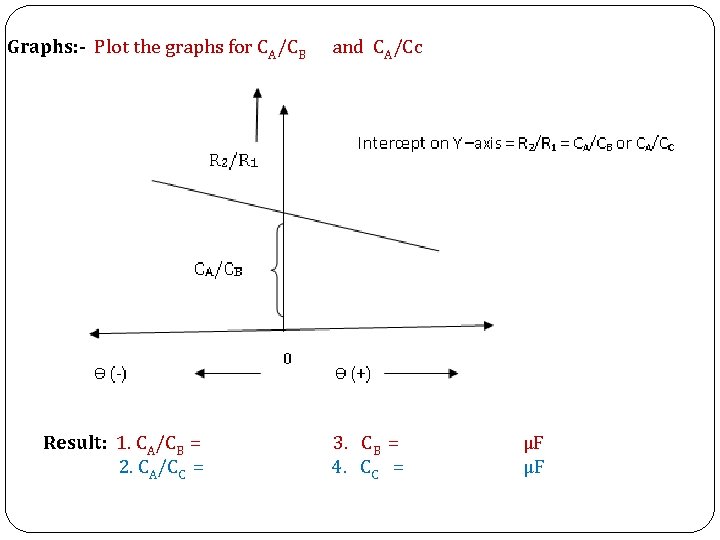
Graphs: - Plot the graphs for CA/CB Result: 1. CA/CB = 2. CA/CC = and CA/Cc 3. CB = 4. CC = µF µF
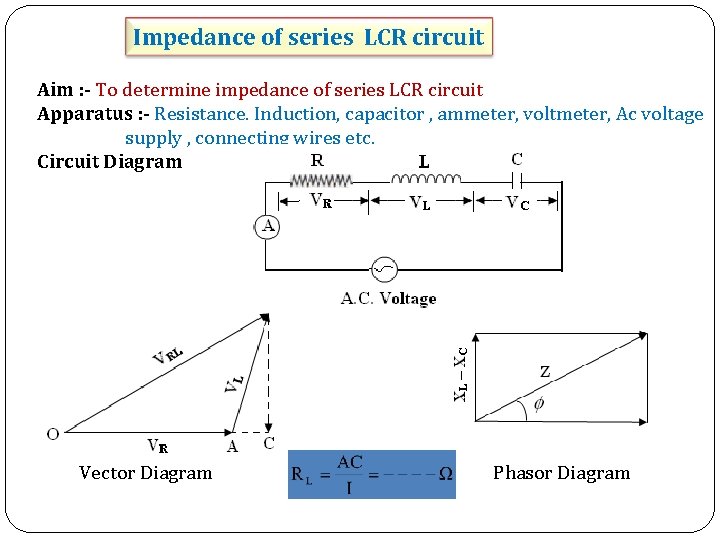
Impedance of series LCR circuit Aim : - To determine impedance of series LCR circuit Apparatus : - Resistance. Induction, capacitor , ammeter, voltmeter, Ac voltage supply , connecting wires etc. Circuit Diagram Vector Diagram Phasor Diagram
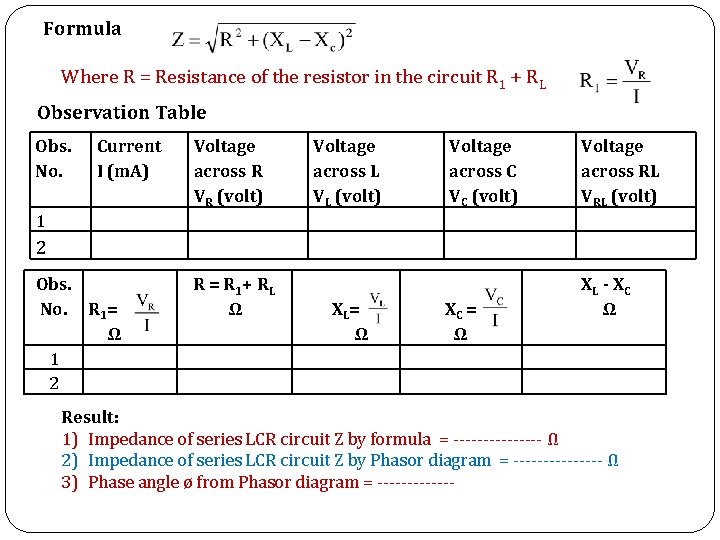
Formula Where R = Resistance of the resistor in the circuit R 1 + RL Observation Table Obs. No. Current I (m. A) Voltage across R VR (volt) Voltage across L VL (volt) Voltage across C VC (volt) Voltage across RL VRL (volt) 1 2 Obs. No. R 1= Ω 1 2 R = R 1+ RL Ω XL= Ω XC = Ω XL - XC Ω Result: 1) Impedance of series LCR circuit Z by formula = -------- Ω 2) Impedance of series LCR circuit Z by Phasor diagram = -------- Ω 3) Phase angle ø from Phasor diagram = -------

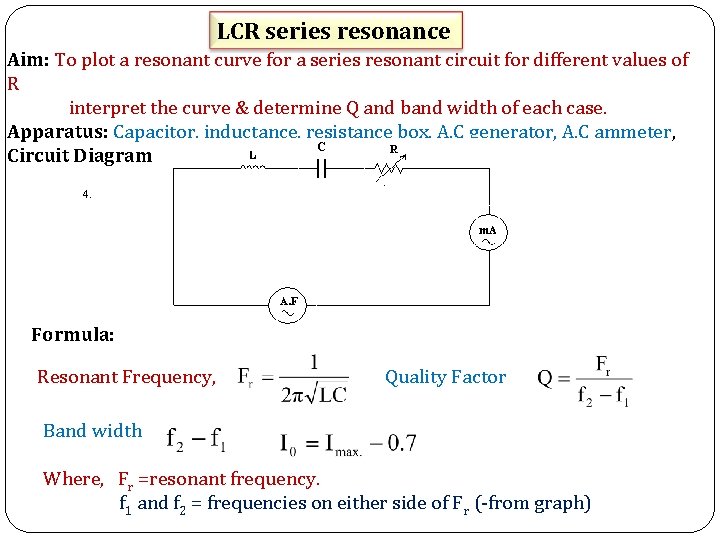
LCR series resonance Aim: To plot a resonant curve for a series resonant circuit for different values of R interpret the curve & determine Q and band width of each case. Apparatus: Capacitor, inductance, resistance box, A. C generator, A. C ammeter, Circuit Diagram 4. Formula: Resonant Frequency, Quality Factor Band width Where, Fr =resonant frequency. f 1 and f 2 = frequencies on either side of Fr (-from graph)
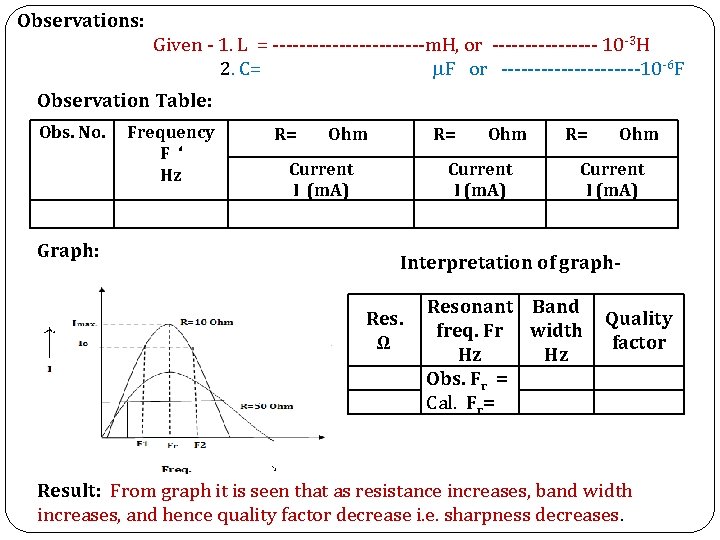
Observations: Given - 1. L = ------------m. H, or -------- 10 -3 H 2. C= F or -----------10 -6 F Observation Table: Obs. No. Graph: Frequency F ‘ Hz R= Ohm R= Current I (m. A) Ohm Current I (m. A) R= Ohm Current I (m. A) Interpretation of graph. Res. Ω Resonant Band freq. Fr width Hz Hz Obs. Fr = Cal. Fr= Quality factor Result: From graph it is seen that as resistance increases, band width increases, and hence quality factor decrease i. e. sharpness decreases.
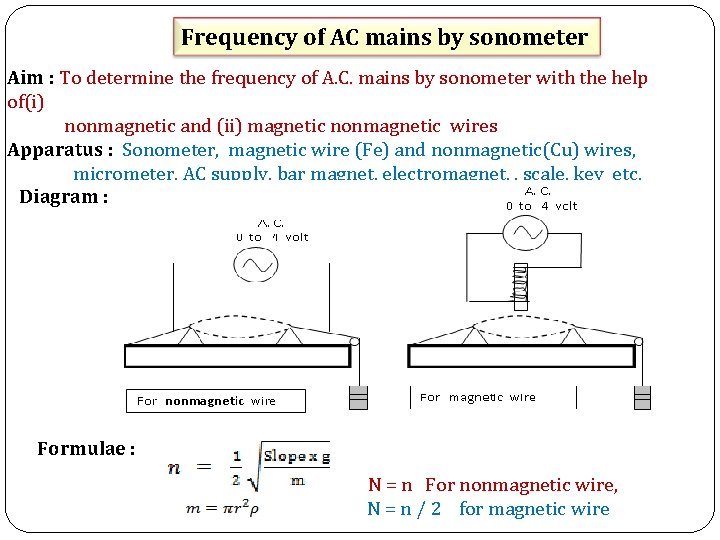
Frequency of AC mains by sonometer Aim : To determine the frequency of A. C. mains by sonometer with the help of(i) nonmagnetic and (ii) magnetic nonmagnetic wires Apparatus : Sonometer, magnetic wire (Fe) and nonmagnetic(Cu) wires, micrometer, AC supply, bar magnet, electromagnet, , scale, key etc. Diagram : Formulae : N = n For nonmagnetic wire, N = n / 2 for magnetic wire
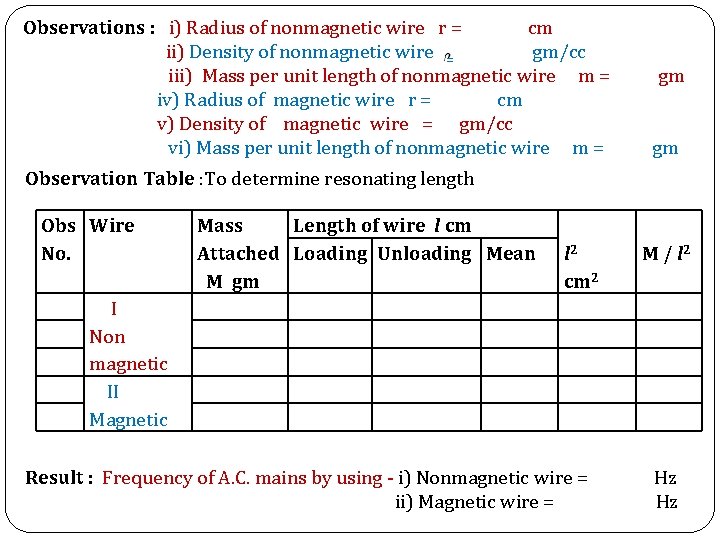
Observations : i) Radius of nonmagnetic wire r = cm ii) Density of nonmagnetic wire = gm/cc iii) Mass per unit length of nonmagnetic wire m = iv) Radius of magnetic wire r = cm v) Density of magnetic wire = gm/cc vi) Mass per unit length of nonmagnetic wire m = gm gm Observation Table : To determine resonating length Obs Wire No. Mass Length of wire l cm Attached Loading Unloading Mean M gm l 2 cm 2 M / l 2 I Non magnetic II Magnetic Result : Frequency of A. C. mains by using - i) Nonmagnetic wire = ii) Magnetic wire = Hz Hz
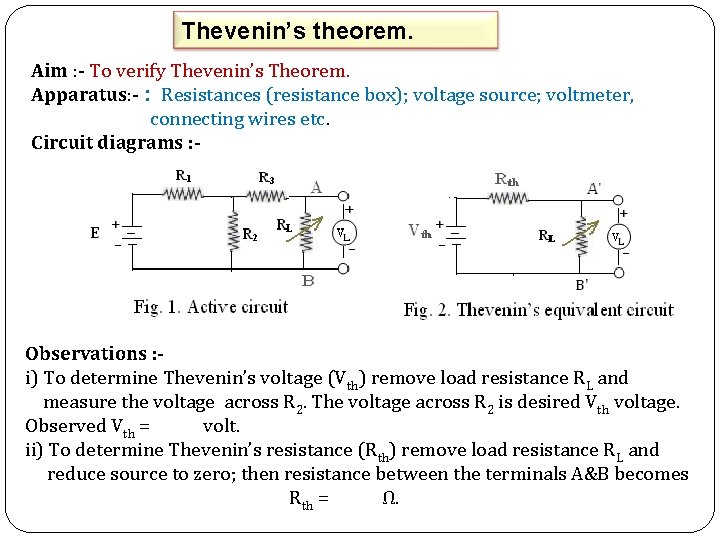
Thevenin’s theorem. Aim : - To verify Thevenin’s Theorem. Apparatus: - : Resistances (resistance box); voltage source; voltmeter, connecting wires etc. Circuit diagrams : - Observations : i) To determine Thevenin’s voltage (Vth) remove load resistance RL and measure the voltage across R 2. The voltage across R 2 is desired Vth voltage. Observed Vth = volt. ii) To determine Thevenin’s resistance (Rth) remove load resistance RL and reduce source to zero; then resistance between the terminals A&B becomes Rth = Ω.
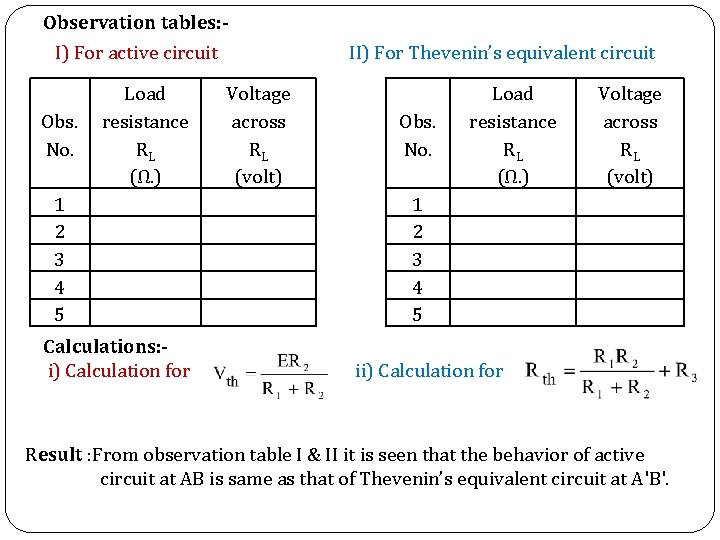
Observation tables: I) For active circuit Obs. No. Load resistance RL (Ω. ) 1 2 3 4 5 Calculations: i) Calculation for Voltage across RL (volt) II) For Thevenin’s equivalent circuit Obs. No. Load resistance RL (Ω. ) Voltage across RL (volt) 1 2 3 4 5 ii) Calculation for Result : From observation table I & II it is seen that the behavior of active circuit at AB is same as that of Thevenin’s equivalent circuit at A'B'.

Thank You
- Slides: 40