Experimental Design for Microarray Studies Kathleen Kerr Department

Experimental Design for Microarray Studies Kathleen Kerr Department of Biostatistics University of Washington

Design: The “Pre-Planning” Stage Before an investigator consults a statistician about design, s/he has probably already made some important design decisions about the types of m. RNA to be studied. • Which treatments to apply? • Under what conditions will m. RNA be collected? These choices are primarily made based on scientific, not statistical, considerations. • Technical consideration: can the samples provide sufficient m. RNA?

The “Pre-Planning” Stage At this point, it is most important to establish realistic expectations for the study. • What are the goals of the experiment? • What do the investigators hope to learn? What will they do with the information?

Is the study an experiment or an observational study? Unfortunately, all microarray studies tend to be called experiments, even when they are observational studies. John Potter Epidemiology, cancer genetics and microarrays: making correct inferences, using appropriate designs TRENDS in Genetics, 2003

Is the study an experiment or an observational study? Answering this question is the first step in understanding the causal inferences that CAN and CANNOT be made. There is a tendency in the microarray literature to make unjustified causal inferences about observed gene expression differences in observational studies.

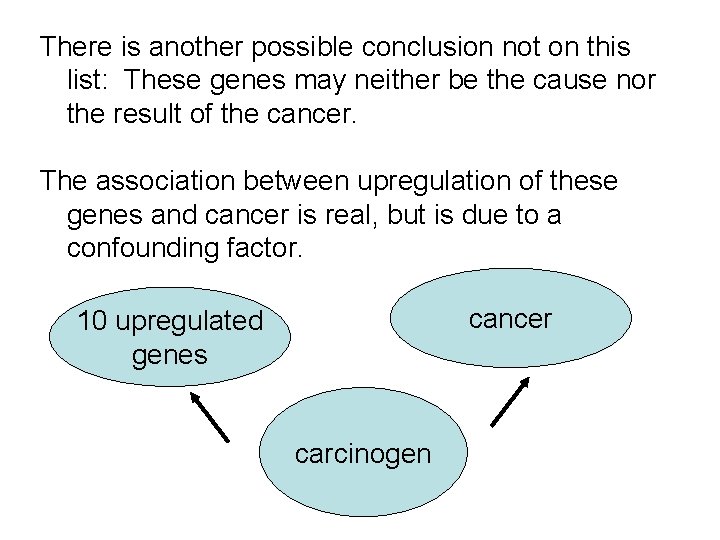
Example: A comparison of the gene expression between cancer patients and control patients who do not have cancer yields ten genes that are significantly and substantially upregulated in the cancer patients. These changes are real and not type I errors – if the study is repeated these ten genes show the same pattern. Possible Conclusions: A. Overactivity in these genes caused the cancer. B. These genes are upregulated as a result of these patients having cancer. C. All of the Above. D. None of the Above.

There is another possible conclusion not on this list: These genes may neither be the cause nor the result of the cancer. The association between upregulation of these genes and cancer is real, but is due to a confounding factor. cancer 10 upregulated genes carcinogen

In general, we should be extremely cautious about making causal inferences from observational studies. (Even when the “observations” are high -tech measurements like gene expression. ) In randomized experiments, there is greater ability to make causal inferences because randomization should eliminate the possibility that observed associations are due to confounding factors.

E. g. , We apply a drug treatment to a randomly selected set of mice and a placebo to another randomly selected set. Because of the randomization, we are justified in making causal inferences: up- or downregulated genes can be inferred to have been caused by the treatment. Caution: This is quite different from causal inferences about the effect of gene expression changes.

Topics in Experimental Design 1. General design principles for microarrays • • Two-color, one-color Three principles of design 2. Design issues for two-color platforms • Blocking 3. Putting it all together • Replication and blocking

General Principles of Statistical Design I. Replication • • II. Means different things in microarrays There are different kinds of replicates with different levels of importance Randomization • Important but often overlooked III. Blocking • Key aspect of design for 2 -color arrays

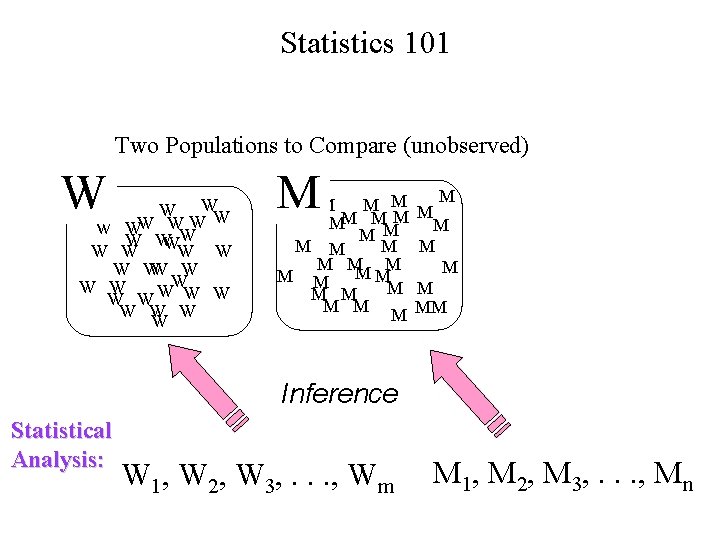
Replication First level of replication: Genes spotted multiple times per array Second level of replication: Multiple arrays to study the samples contrast with: Replication in the classical sense: Random sampling of individuals from the populations of interest or randomly assigning individuals to treatment groups.

Statistics 101 Two Populations to Compare (unobserved) W W WW W W W W W W M M M M MM M M M observed: M M MM e pl m a S M W 1, W 2, W 3, . . . , Wm e pl m a S M 1, M 2, M 3, . . . , Mn

Statistics 101 Two Populations to Compare (unobserved) W W WW W W W W W W M M MM M M M M MM Inference Statistical Analysis: W 1, W 2, W 3, . . . , Wm M 1, M 2, M 3, . . . , Mn

We may at once admit that any inference from the particular to the general must be attended with some degree of uncertainty, but this is not the same as to admit that such inference cannot be absolutely rigorous, for the nature and degree of the uncertainty may itself be capable of rigorous expression. — R. A. Fisher Statistician Geneticist

Replication Measurement Error/ Technical Error First level of replication: Genes spotted multiple times per array Second level of replication: Multiple arrays to study the samples replication Biological Variability repeated measures / subsampling Replication in the classical sense: Random sampling of individuals from the populations of interest or randomly assigning individuals to treatment groups. Without this kind of replication, inference is limited to the particular RNAs in the study.

Repeated measurements through multiple slides and/or multiple spots is useful for controlling measurement error. However, these can never substitute for biological replication – they do not provide information for making the desired inferences.

Technical replicates, while useful, are not necessary in most experiments. Biological replicates are more useful. Heuristically, biological replicates provide information about both technical and biological variation; technical replicates provide information only about technical variation.

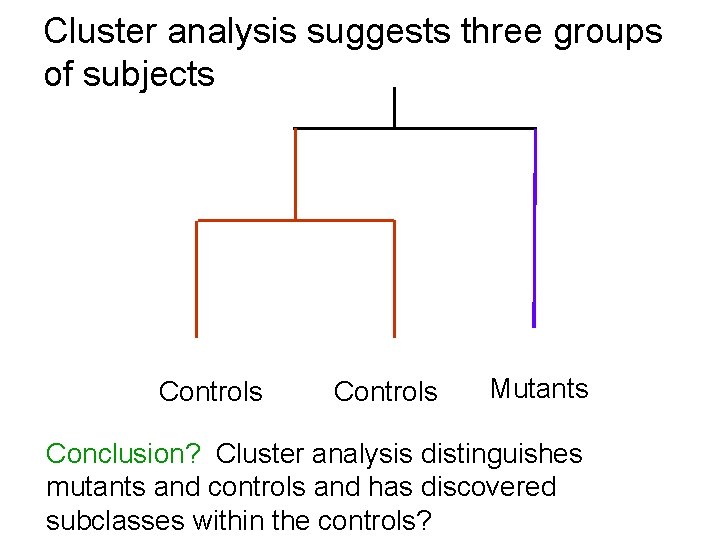
To introduce the next topic: An example and a word of caution Experiment: 30 RNAs – 10 carriers of a mutation – 20 controls • expression analysis on a single-channel platform • limited to 10 hybridizations in 1 day, so the study was carried out over 3 days

Cluster analysis suggests three groups of subjects Controls Mutants Conclusion? Cluster analysis distinguishes mutants and controls and has discovered subclasses within the controls?

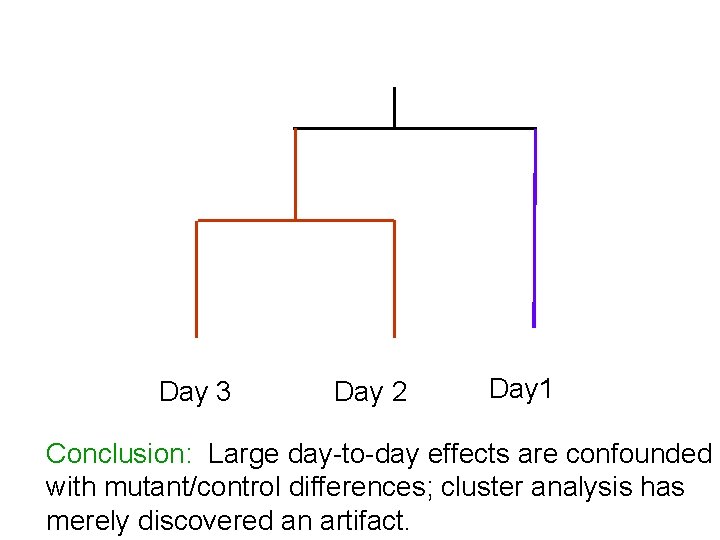
Day 3 Day 2 Day 1 Conclusion: Large day-to-day effects are confounded with mutant/control differences; cluster analysis has merely discovered an artifact.

experimental plan: Day 1: 10 mutants Day 2: 10 controls Day 3: 10 remaining controls

Randomization Once an experimental design has been chosen, everything possible (practical) should be randomized. • Randomize animals into treatment/control or dosage group. • Randomly choose arrays from batch of arrays for each hybridization. Randomization controls unanticipated systematic biases.

Blocking is a design technique for dealing with known sources of variation (contrast with randomization, which addresses unanticipated sources of variation)

Blocking Scientists routinely and intuitively apply the principle of blocking in all their experiments: • If an assay is known to be affected by humidity, conduct all assays on samples to be compared at the same time, when humidity is effectively constant • Compare a new ocular treatment with placebo by applying one of each to each eye of multiple individuals. Allows “within individual” evaluation of the treatment

With two-color array platforms, “blocking” is built into the system. . .

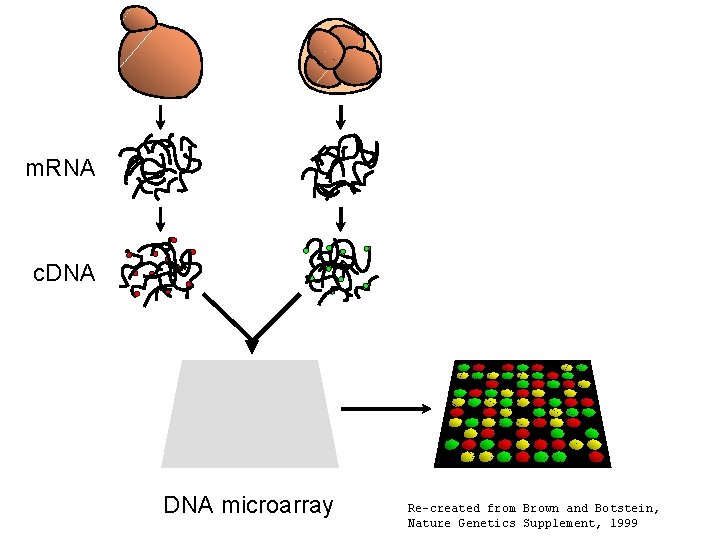
m. RNA c. DNA microarray Re-created from Brown and Botstein, Nature Genetics Supplement, 1999

Because of spot-to-spot variation, the amount of red or green signal could reflect the amount of transcript OR simply the amount of probe available for hybridization. However, aside from the spot characteristics, the relative size of the red and green signal should be informative about the relative amount of transcript in the two samples. Loosely, we can think of two-color arrays as a “comparison” between a pair of RNAs.

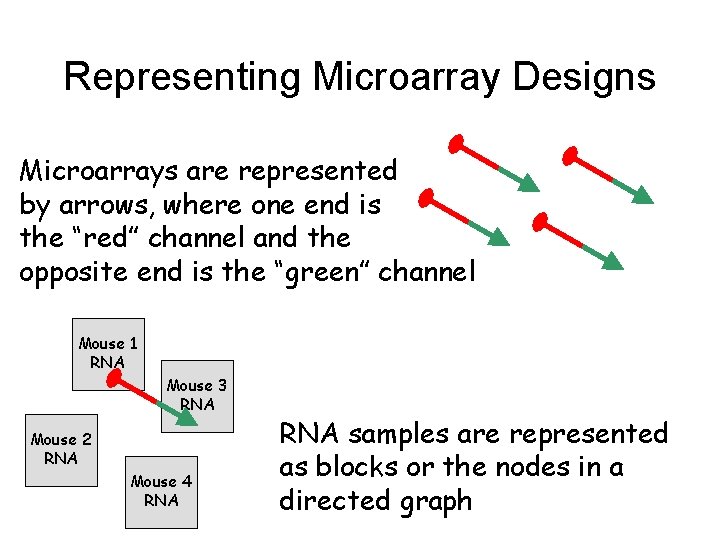
Representing Microarray Designs Microarrays are represented by arrows, where one end is the “red” channel and the opposite end is the “green” channel Mouse 1 RNA Mouse 3 RNA Mouse 2 RNA Mouse 4 RNA samples are represented as blocks or the nodes in a directed graph

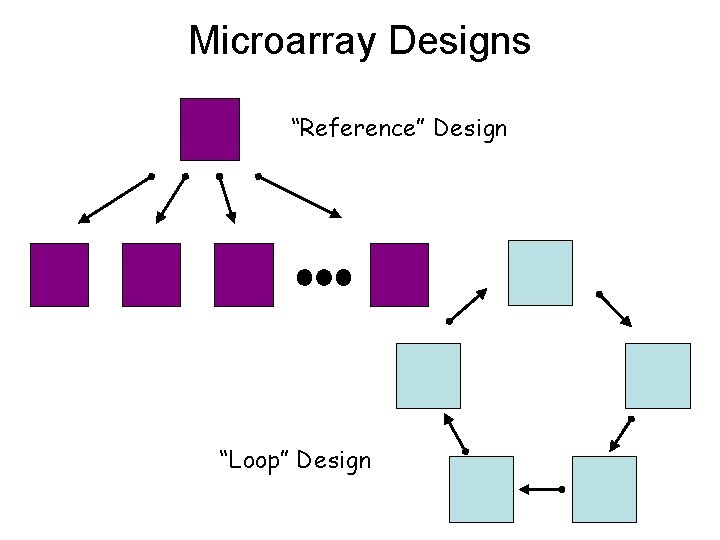
Microarray Designs “Reference” Design “Loop” Design

Kerr and Churchill (Biostatistics, 2001) compared the relative efficiency of different experimental layouts for making inference about gene expression in the assayed RNAs. For example, the loop design is more efficient than the reference design for up to 10 RNAs. Then loops get too big and reference design are more efficient.

However, this does not address the question that is important for most studies: how does gene expression differ between two or more populations?

How do we combine biological replicates, which are crucial for making the desired inference, with the blocking structure of a two-color platform?

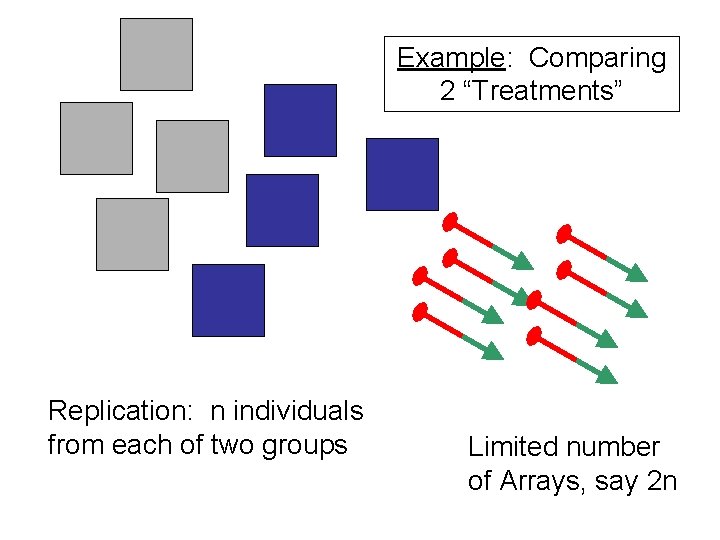
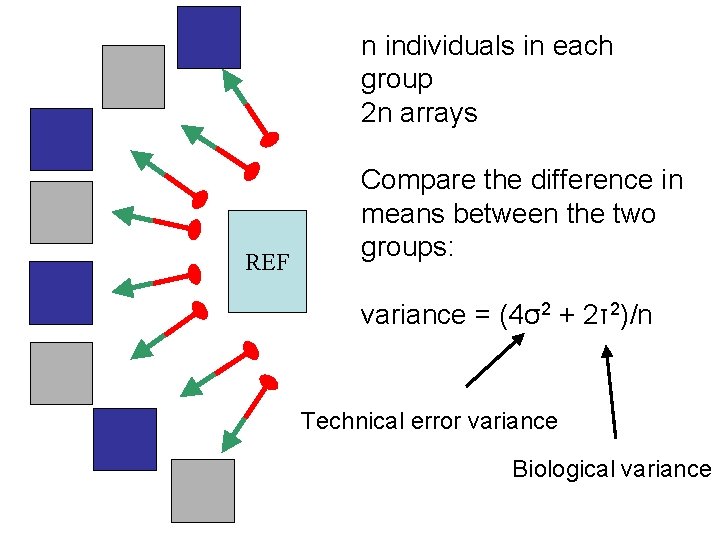
Example: Comparing 2 “Treatments” Replication: n individuals from each of two groups Limited number of Arrays, say 2 n

n individuals in each group 2 n arrays REF Compare the difference in means between the two groups: variance = (4σ2 + 2τ2)/n Technical error variance Biological variance

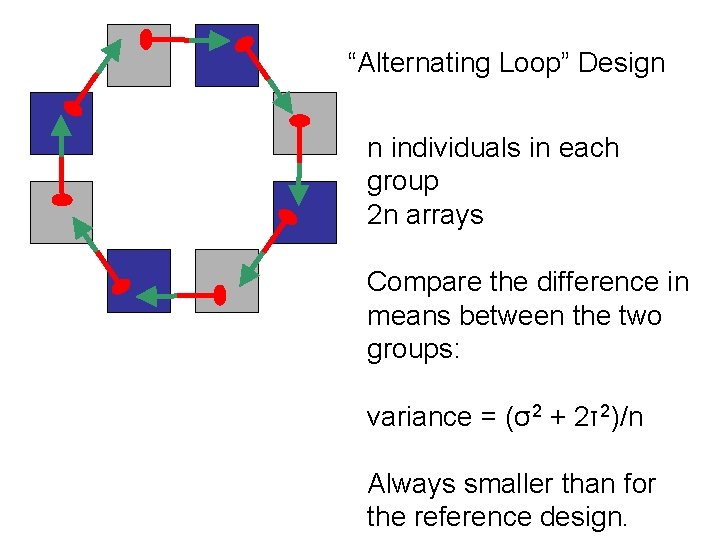
“Alternating Loop” Design n individuals in each group 2 n arrays Compare the difference in means between the two groups: variance = (σ2 + 2τ2)/n Always smaller than for the reference design.

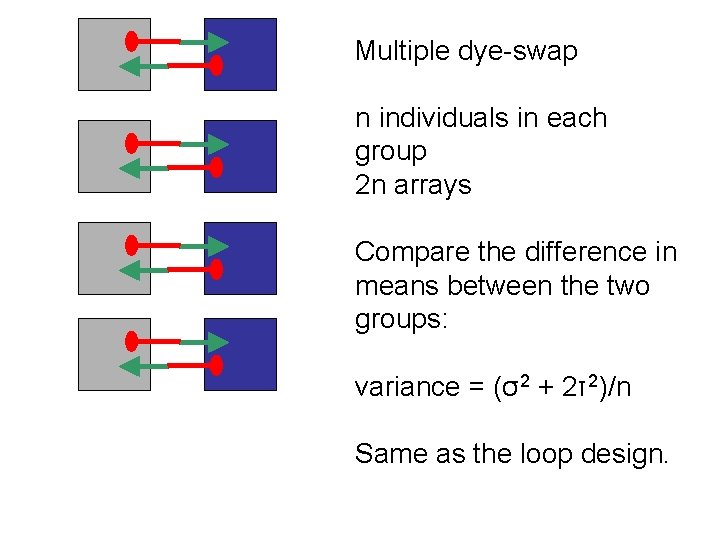
Multiple dye-swap n individuals in each group 2 n arrays Compare the difference in means between the two groups: variance = (σ2 + 2τ2)/n Same as the loop design.

(σ2 + 2τ2) is always less than (4σ2 + 2τ2). However, if biological variability is high then the efficiency advantage of the loop is diminished. In analyzing data from any of these designs, it is crucial that different kinds of replicates are treated differently. Inference should be based on biological variability, not technical error.

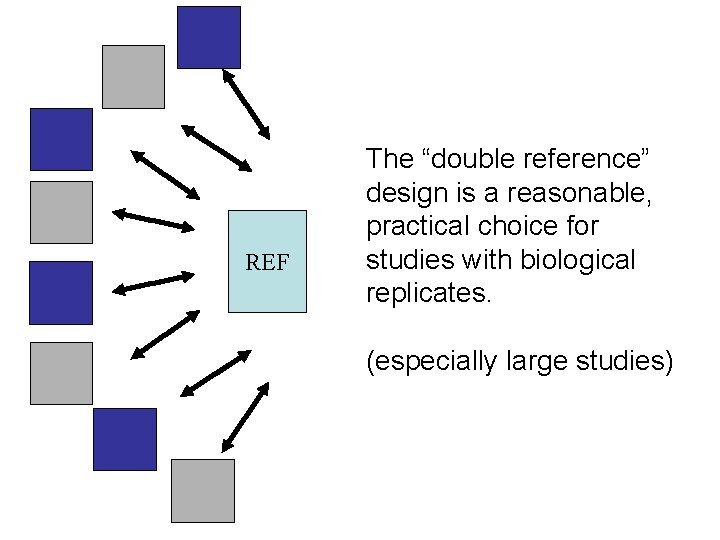
REF The “double reference” design is a reasonable, practical choice for studies with biological replicates. (especially large studies)

Generally, we want efficient designs for an appropriate criterion but we should consider other aspects of good design: • • Robust properties Extendibility Simplicity of execution Useful sub-designs

• Robust properties What happens to the efficiency if we lose an array? If we lose some spots on every array? • Extendibility What if we decide to add more samples to the study later? • Simplicity of execution Will we be able to keep track of the assays we need to do? • Useful sub-designs What if we want to analyze the data on just a subset of samples?

An invited speaker at RECOMB 2001 in Montreal made the following observation and comment (paraphrase): Some scientists talk about microarray data today the way some scientists used to talk about computers in the 1960’s. They seemed to think that, once computers became powerful enough, they would – by some unspecified mechanism – suddenly become intelligent. That is, scientists talk with awe about the masses of data produced by microarrays. There seems to be an unspoken notion that once enough data are collected, we will – by some unspecified mechanism – know everything about the underlying biology.

It doesn’t work that way! Lots of Data do not necessarily mean Lots of Information! Microarrays are still just a measurement tool – it still takes carefully designed experiments and careful data analysis to use this tool to learn more about biology.

A final word on design: “To call in the statistician after the experiment is done may be no more than asking him to perform a postmortem examination: he may be able to say what the experiment died of. '' -R. A. Fisher, ca 1938

Summary • Make sure expectations are realistic – Experiment or observational study? • Replication is useful at all levels, but biological replicates trump technical replicates – In most studies, all replicates should be biological replicates – If the design has both kinds of replicates, the analysis must treat different kinds of replicates differently • Randomize, randomize. . . • Blocking is a key feature of two-color array experimental design • The design of a microarray experiment is the most important determinant of the success of the study – Unlike a bad analysis, you cannot recover from a bad design