Experiment Simulation Thermal Diffuse Scattering Si 300 K

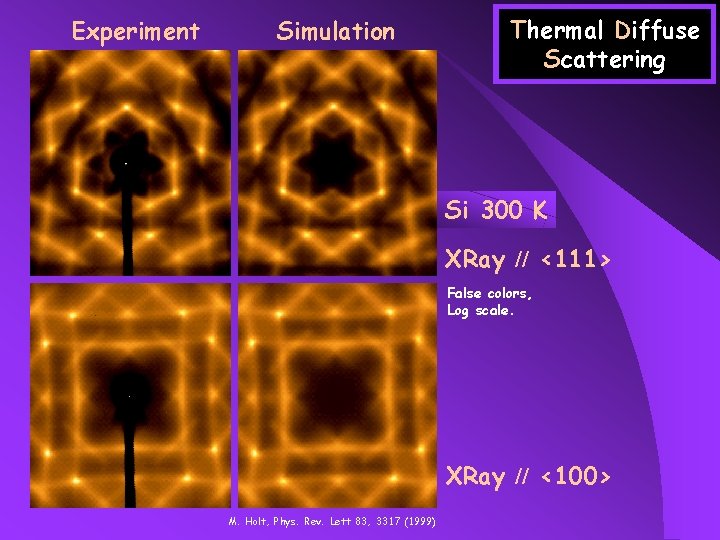
Experiment Simulation Thermal Diffuse Scattering Si 300 K XRay // <111> False colors, Log scale. XRay // <100> M. Holt, Phys. Rev. Lett 83, 3317 (1999)

TDS calculation-1 One atom per cell Harmonic theory: At first order, displacement-displacement correlations

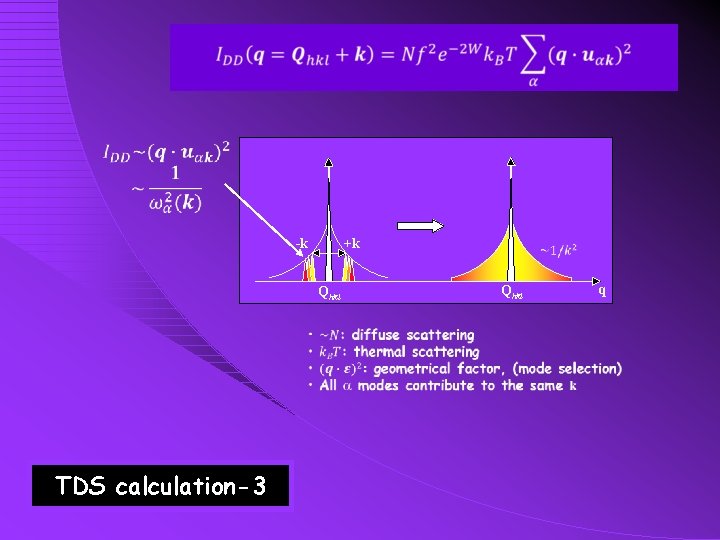
-k +k Qhkl TDS calculation-3 q

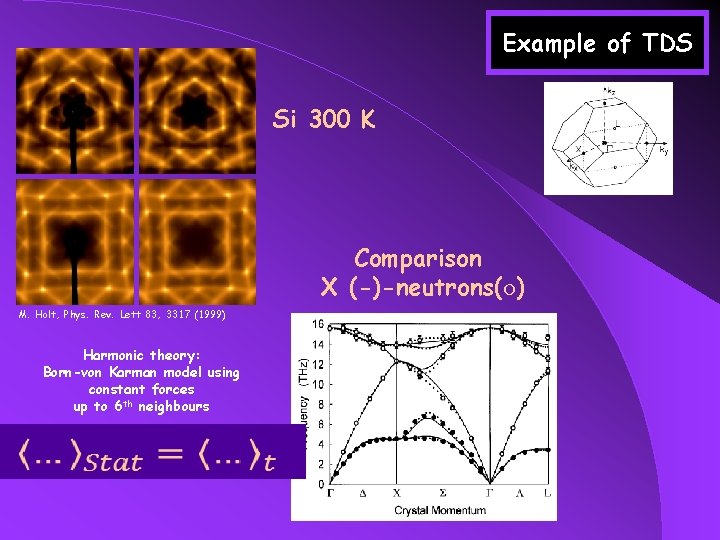
Example of TDS Si 300 K Comparison X (-)-neutrons(o) M. Holt, Phys. Rev. Lett 83, 3317 (1999) Harmonic theory: Born-von Karman model using constant forces up to 6 th neighbours

Substitution disorder Alloy or solid solution Ax. B 1 -x No information on correlations • Case of total disorder Laue scattering:

Correlations Conditional probabilities AB pairs = BA pairs Short-range order: Warren-Cowley parameters B A

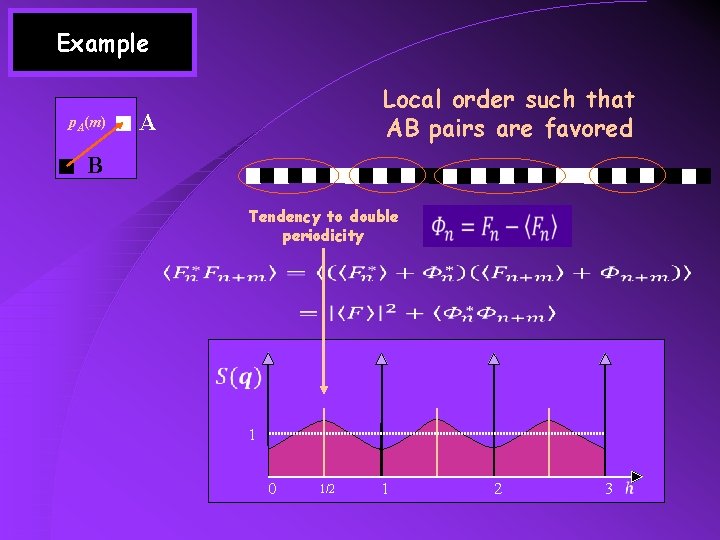
Example p. A(m) Local order such that AB pairs are favored A B Tendency to double periodicity 1 0 1/2 1 2 3

Conclusion

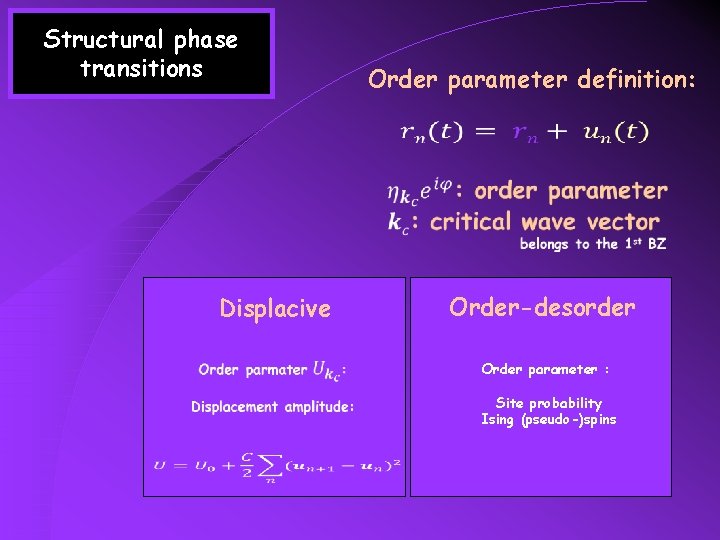
Structural phase transitions Order parameter definition: Displacive Order-desorder Order parameter : Site probability Ising (pseudo-)spins

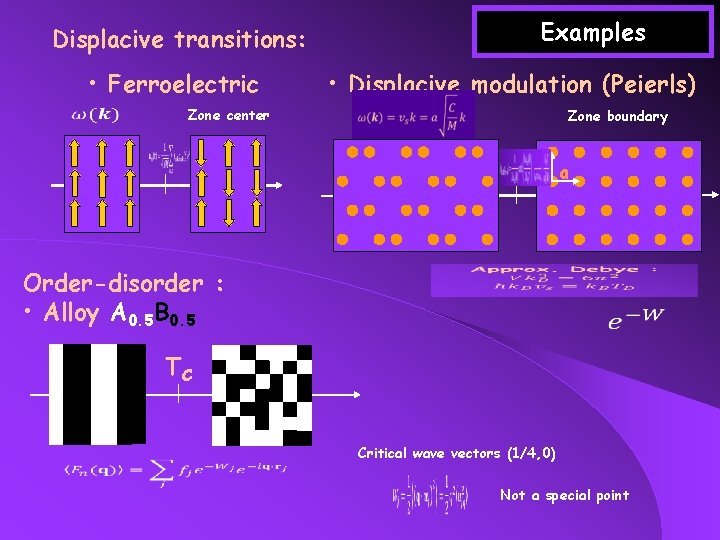
Examples Displacive transitions: • Ferroelectric Zone center • Displacive modulation (Peierls) Zone boundary b a Order-disorder : • Alloy A 0. 5 B 0. 5 TC Critical wave vectors (1/4, 0) Not a special point

Displacive transition Ordre parameter fluctuations Susceptibility associated to order parameter

Fluctuation-dissipation Example of phonons: Par le théorème d’équipartition de l’énergie

Calculation of the intensity Fluctuation-dissipation

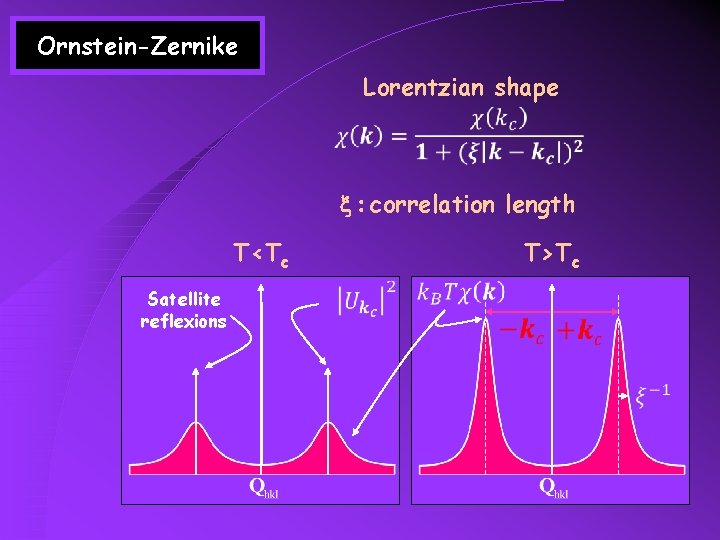
Ornstein-Zernike Lorentzian shape x : correlation length T<Tc Satellite reflexions T>Tc

Critical exponents LRO QLRO SRO

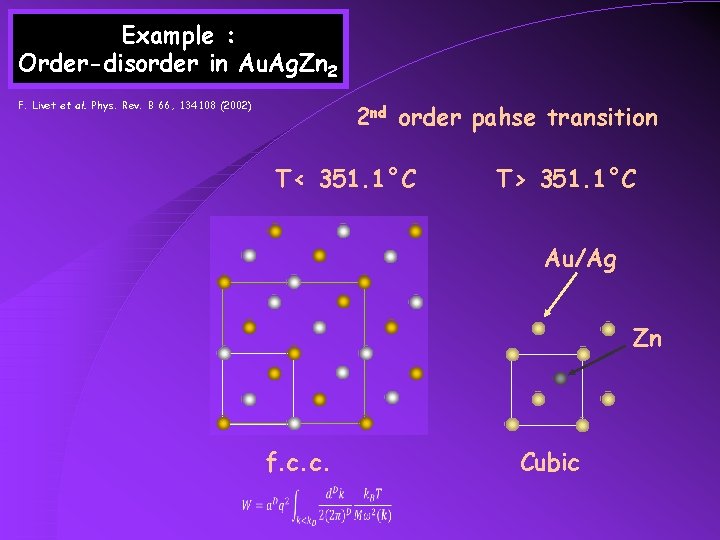
Example : Order-disorder in Au. Ag. Zn 2 F. Livet et al. Phys. Rev. B 66, 134108 (2002) 2 nd order pahse transition T< 351. 1°C T> 351. 1°C Au/Ag Zn f. c. c. Cubic

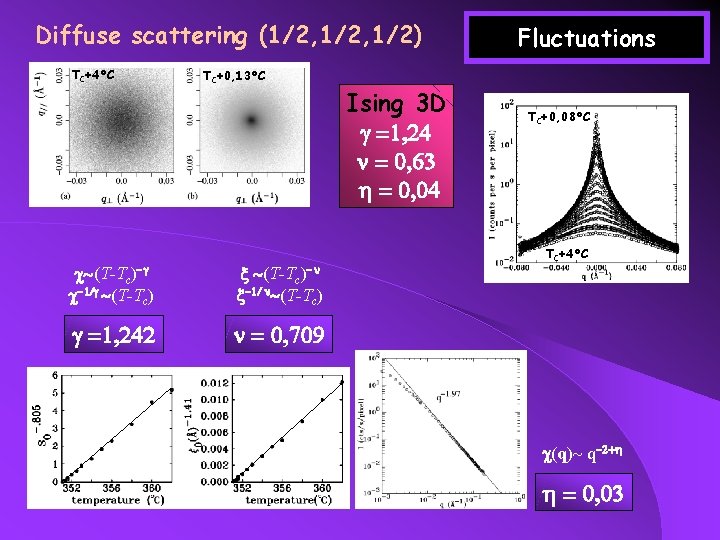
Diffuse scattering (1/2, 1/2) TC+4°C TC+0, 13°C c~(T-Tc)-g c-1/g ~(T-Tc) x ~(T-Tc)-n x-1/ n~(T-Tc) g =1, 242 n = 0, 709 Ising 3 D g =1, 24 n = 0, 63 h = 0, 04 Fluctuations TC+0, 08°C TC+4°C c(q)~ q-2+h h = 0, 03

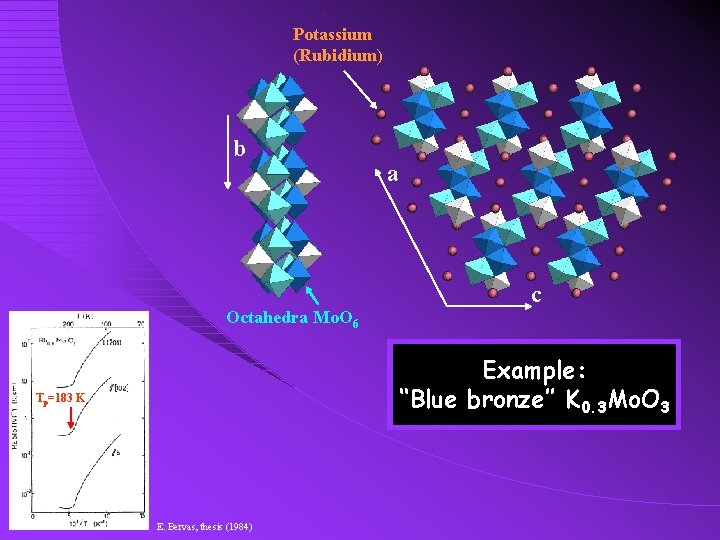
Potassium (Rubidium) b a c Octahedra Mo. O 6 Example: ‘‘Blue bronze’’ K 0. 3 Mo. O 3 Tp=183 K E. Bervas, thesis (1984)

Blue bronze At T=183 K: appareance of sattelite reflexions at the critical wave vector:

Determination of interatomic potential Ex: Ising model Within mean field appr. the susceptibility is:

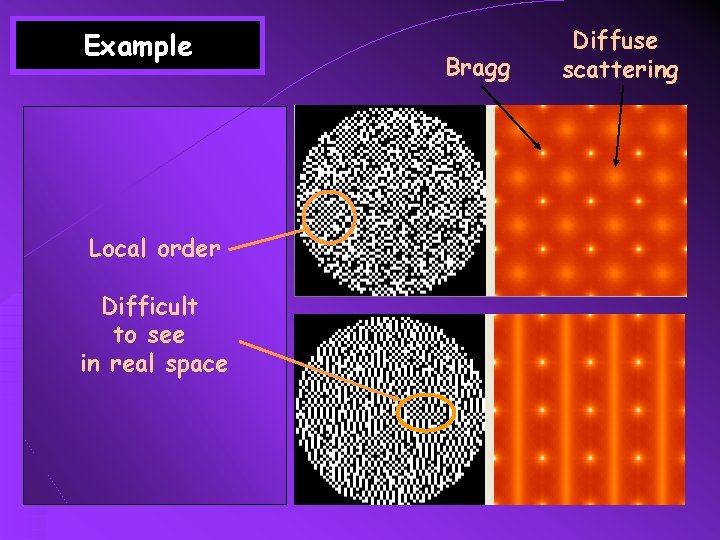
Example Isotrope Ji=Jj Local order Difficult to see in real space Anisotrope (1 D) 100 x. Ji=Jj Bragg Diffuse scattering