Experiment No 3 Electric Current Resistance and Ohms

Experiment No. 3 Electric Current, Resistance and Ohm’s Law • • • • Electromotive Force emf and terminal voltage Batteries in series and parallel Circuit diagrams and Symbols Resistors and Ohm’s Law Resistivity Electric power Calculate resistance, current voltage and electric power Conduct experiments using resistors Measure resistance, current and voltage in each circuit arrangement Test Data Sheet Learn how to analyze test results Quiz No. 3 Homework New Terminology 1

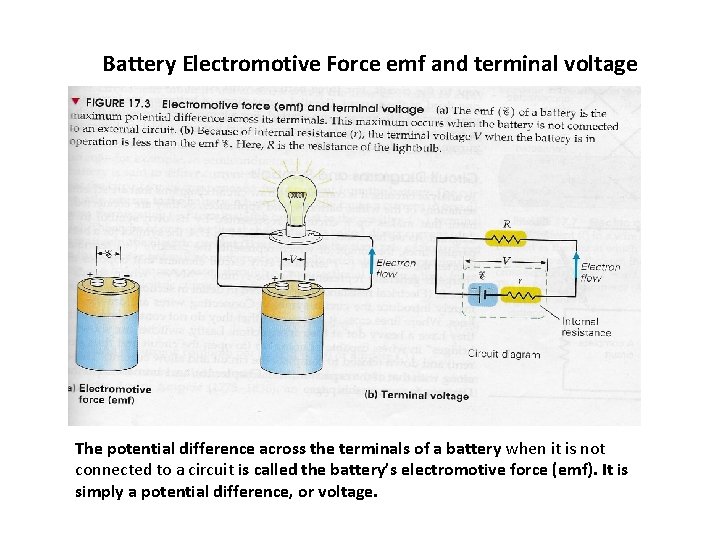
Battery Electromotive Force emf and terminal voltage The potential difference across the terminals of a battery when it is not connected to a circuit is called the battery’s electromotive force (emf). It is simply a potential difference, or voltage.

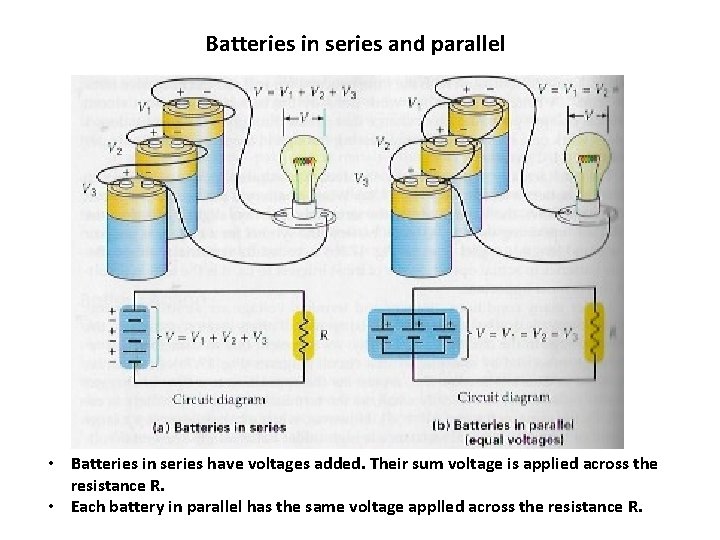
Batteries in series and parallel • Batteries in series have voltages added. Their sum voltage is applied across the resistance R. • Each battery in parallel has the same voltage applled across the resistance R.

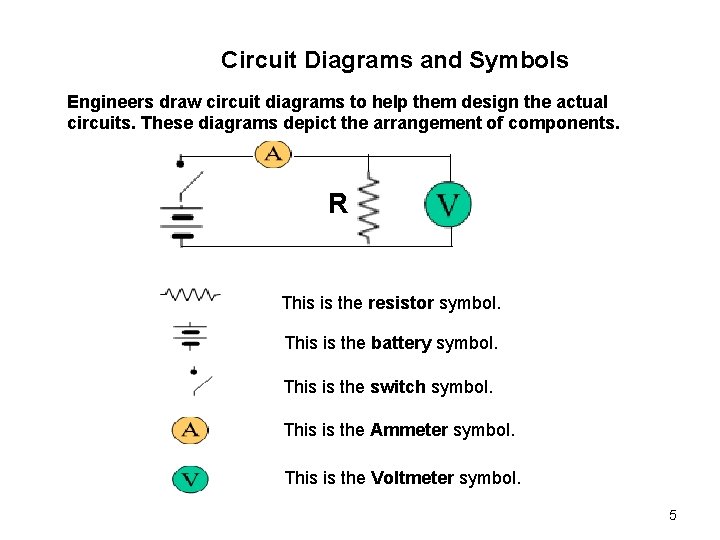
Circuit Diagrams and Symbols Engineers draw circuit diagrams to help them design the actual circuits. These diagrams depict the arrangement of components. R This is the resistor symbol. This is the battery symbol. This is the switch symbol. This is the Ammeter symbol. This is the Voltmeter symbol. 5

Open, Closed, and Short Circuits • What is an OPEN or CLOSED circuit? OPEN is a term used by engineers to describe the circuit condition where current is not flowing (e. g. , a switch is in the open position or a light bulb has a broken filament). A circuit must be CLOSED for current to flow allowing the circuit to perform its intended function (e. g. , a light switch is in the closed position allowing the light to function). • What is a SHORT circuit? SHORT is a term used by engineers to describe the effect of inadvertent connection of two power supply outlets (plus and minus). A short circuit means that there is a short path between battery terminals, or almost no resistance between them. This causes unintended heating and sometimes “arcs and sparks” that can damage equipment. 6

Electric Current, I = q/t [C/s = As/s = A] R Electric current is defined as the time rate of flow of an electric charge.

What's a Resistor? A resistor is any material that electric current cannot travel through easily. When electricity is forced through a resistor, often the energy in the electricity is changed into another form of energy, such as light or heat. The reason a light bulb glows is that electricity is forced through tungsten, which is a resistor. The energy is released as light and heat. An Ohm is a unit used to measure the resistance value of a resistor. It is named for scientist Georg Ohm who did research on materials with resistive characteristics. A conductor is the opposite of a resistor. Electricity travels easily and efficiently through a conductor. 8

Ohm’s Law • Ohm’s Law establishes the relationship between voltage V, resistance R and electric current I in an electric circuit. • When a voltage, V is applied in the same circuit an electric current, I flows and it is limited only by the circuit resistance, R. or V =Rx. I or Voltage = Resistance x Current R is the resistance, measured in Ohms. Its symbol is V is the voltage measured in Volts. I is the current measured in Amperes. 1 Ohm = 1 Volt/Ampere Ohm’s Law states that in a circuit with a given resistance the electric current is directly proportionally to the applied voltage. 9

Resistivity (r) and Resistance (R) Electrical resistance is a property of a conductor that opposes the flow of electric current through it. An object of uniform cross section has a resistance proportional to its resistivity and length and is inversely proportional to its cross-sectional area. L Resistance, R = ρ x -----A Units: Resistivity, ρ [ Length, Area, m] L [m] A [m 2] Example: If a 1 m × 1 m solid cube of material has sheet contacts on two opposite faces, and the resistance between these contacts is 1 Ω, then the resistivity of the material is 1 Ω⋅m. 10

Table 1 Material Resistivity, ρ (Ω·m) at 20 °C Carbon (graphene) 1× 10− 8 Silver 1. 59× 10− 8 Copper 1. 68× 10− 8 Annealed copper 1. 72× 10− 8 Gold 2. 44× 10− 8 Aluminium 2. 82× 10− 8 Calcium 3. 36× 10− 8 Tungsten 5. 60× 10− 8 Zinc 5. 90× 10− 8 Nickel 6. 99× 10− 8 Lithium 9. 28× 10− 8 Iron 1. 0× 10− 7 Platinum 1. 06× 10− 7 Tin 1. 09× 10− 7 Carbon steel (1010) 1. 43 x 10− 7 Lead 2. 2× 10− 7 Titanium 4. 20× 10− 7 Sea water 2× 10− 1 Drinking water 2× 101 to 2× 103 Glass 10× 1010 to 10× 1014 11

R Electric Power Electrons are given energy by the battery. As electric charges pass through the circuit they collide with resistor’s atoms and lose energy. The energy transferred through the collisions is transformed into thermal energy. Travelling around a complete circuit any electric charge loses all its potential energy by the time it returns to the battery. Work: W = q. V The rate of energy delivery, Power: P = W/t = q. V/t = IV Example No. 1: If electric power, P is equal to V x I and V = I x R what is R equal to _____? No. 2: If the voltage V = 12 V and the power, P = 5 Watts what is the resistance R equal to? _____ No. 3: A refrigerator runs 15% of time; Power used by the refrigerator is 500 W; Edison charges $ 0. 11 per kilowatt-hour; How much does it cost to operate it monthly (30 days)? Answer: t= 3. 6 hr/day; W= Pxt = 500 x 1. 8 = 1. 8 k. Whr; ; Cost is 1. 8 x 0. 11 x 30 = $5. 94/month

Calculate resistance, current, voltage and power Solve the four problems listed below as applied to the electric circuit diagram below. R Problem No. 1: I = 6 Amps; V = 6 Volts; R = _______ No. 2: V = 6 Volts; R = 10 I =______ No. 3: If electric power, P is equal to V x I and V = I x R what is R equal to _____? No. 4: If the voltage V = 12 V and the power, P = 5 Watts, what is the resistance R equal to? ______ 13

Resistors In Series • SERIES CIRCUITS – The current that flows in a series circuit flows through every component in the circuit. – All the components in a series connection carry the same current. Rtot = R 1 + R 2 + R 3 +………. Rn 14

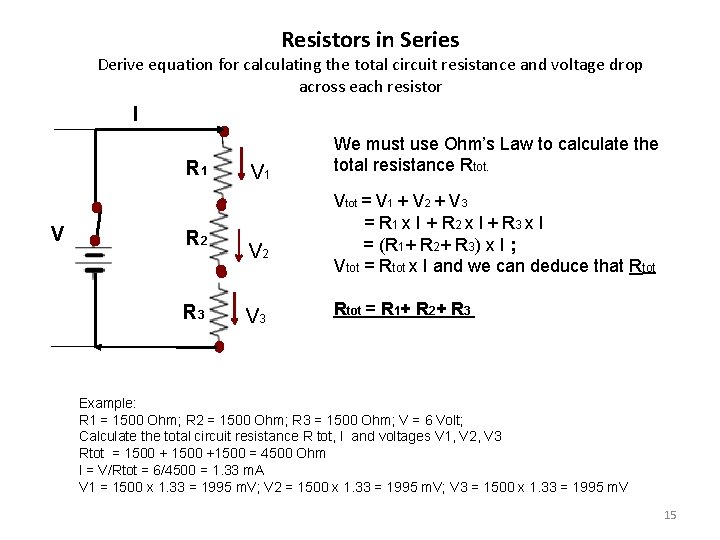
Resistors in Series Derive equation for calculating the total circuit resistance and voltage drop across each resistor I R 1 V R 2 R 3 V 1 V 2 V 3 We must use Ohm’s Law to calculate the total resistance Rtot. Vtot = V 1 + V 2 + V 3 = R 1 x I + R 2 x I + R 3 x I = (R 1+ R 2+ R 3) x I ; Vtot = Rtot x I and we can deduce that Rtot = R 1+ R 2+ R 3 Example: R 1 = 1500 Ohm; R 2 = 1500 Ohm; R 3 = 1500 Ohm; V = 6 Volt; Calculate the total circuit resistance R tot, I and voltages V 1, V 2, V 3 Rtot = 1500 +1500 = 4500 Ohm I = V/Rtot = 6/4500 = 1. 33 m. A V 1 = 1500 x 1. 33 = 1995 m. V; V 2 = 1500 x 1. 33 = 1995 m. V; V 3 = 1500 x 1. 33 = 1995 m. V 15

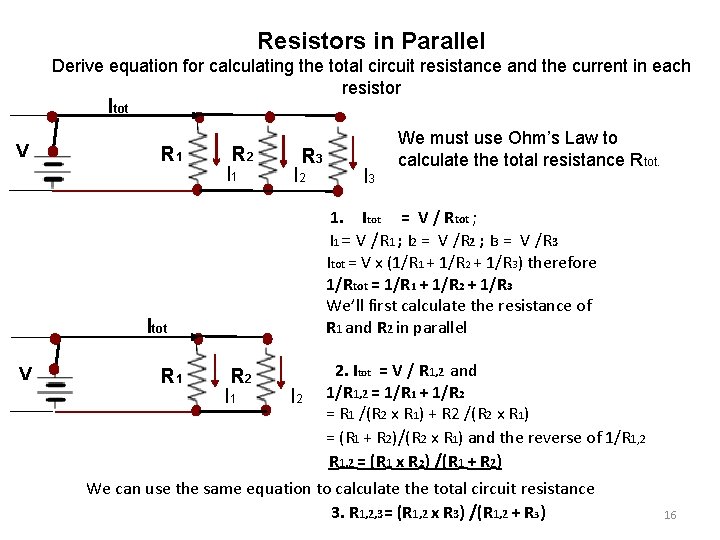
Resistors in Parallel Derive equation for calculating the total circuit resistance and the current in each resistor Itot V R 1 R 2 I 1 R 3 I 2 1. Itot = V / Rtot ; I 1 = V /R 1 ; I 2 = V /R 2 ; I 3 = V /R 3 Itot = V x (1/R 1 + 1/R 2 + 1/R 3) therefore 1/Rtot = 1/R 1 + 1/R 2 + 1/R 3 We’ll first calculate the resistance of R 1 and R 2 in parallel Itot V R 1 I 3 We must use Ohm’s Law to calculate the total resistance Rtot. R 2 I 1 I 2 2. Itot = V / R 1, 2 and 1/R 1, 2 = 1/R 1 + 1/R 2 = R 1 /(R 2 x R 1) + R 2 /(R 2 x R 1) = (R 1 + R 2)/(R 2 x R 1) and the reverse of 1/R 1, 2 = (R 1 x R 2) /(R 1 + R 2) We can use the same equation to calculate the total circuit resistance 3. R 1, 2, 3= (R 1, 2 x R 3) /(R 1, 2 + R 3) 16

Calculation of Series and Parallel Resistances R 1 and R 2 in Series R 1 and R 2 in Parallel Example no. 1: R 1 = 1500 Ohm = 1. 5 KOhm R 2 = 1500 Ohm = 1. 5 Kohm R 1, 2 = R 1+ R 2 R 1, 2 = (R 1 x R 2) /(R 1 + R 2) R 1, 2 = 3, 000 Ohm = 3 Kohm R 1, 2 = _1. 5 x 1. 5 3 = 0. 75 Kohm = 750 Ohm Example no. 2: R 1 = 1500 Ohm = 1. 5 KOhm R 2 = 470 Ohm = 0. 47 KOhm R 1, 2 =1, 970 Ohm =1. 97 Kohm R 1, 2 = 1. 5 x 0. 47 1. 97 = 0. 36 Kohm = 360 Ohm Resistors in SERIES increase total circuit resistance. Resistors in PARALLEL reduce total circuit resistance. 17

Test No. 1 Resistors in Series R 1 a 1 to a 5 R 2 R 3 Four resistors are connected in SERIES with each other Connect the four 1500 Ohm resistors R 1, R 2, R 3 and R 4 as shown. b 5 to b 10 a 10 to a 15 b 15 to b 20 R 4 Measure the resistance using the 20 K resistance scale on the meter. Expected Actual R 1 = _______; _______ R 1 + R 2 + R 3 + R 4 = _______; _______ Note: Enter your Test No. 1 four resistors data on the Data Sheet Pg. 23 18

Test No. 2 Resistors in Parallel R 1 a 1 to a 5 R 3 R 2 R 4 b 1 to b 5 Two Resistors are connected in PARALLEL with each other. Each of the two pairs is in SERIES with the other pairs. Connect the four 1500 Ohm resistors R 1, R 2, R 3 and R 4 as shown. Measure the resistance using the 20 K resistance scale. Expected Actual (R 1 & R 2) = ______ (R 1 & R 2) + (R 3 & R 4)=______ Note: Enter your Test 2 data on the Data Sheet (pg. 23) 19

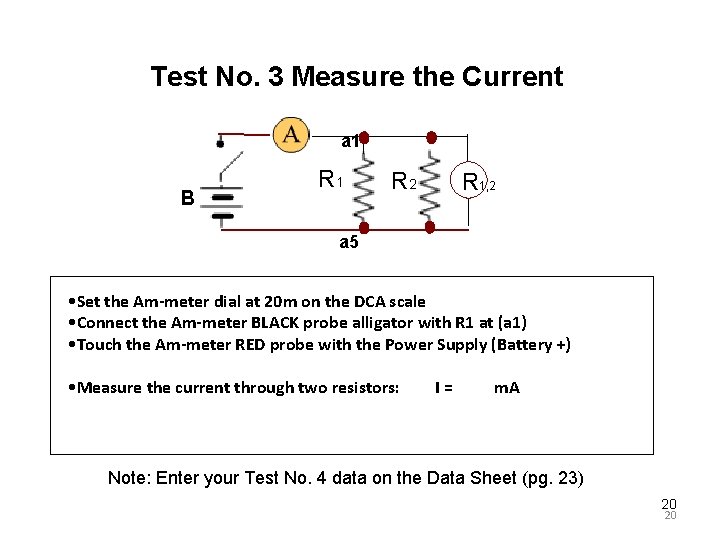
Test No. 3 Measure the Current a 1 B R 1 R 2 R 1, 2 a 5 • Set the Am-meter dial at 20 m on the DCA scale • Connect the Am-meter BLACK probe alligator with R 1 at (a 1) • Touch the Am-meter RED probe with the Power Supply (Battery +) • Measure the current through two resistors: I= m. A Note: Enter your Test No. 4 data on the Data Sheet (pg. 23) 20 20

Calculate the Current a 1 R 1 B I V a 5 Power supply voltage: 5. 8 to 6. 4 V (Why the variation? ) Resistor R 1: 1425 to 1575 Ohm (Why the variation? ) Current, I = V R 1 = ? I = V = _6_ = 0. 004 A = 4. 0 m. A (nominal) R 1 1500 Note: Enter your calculated current value under Test 3 on the Data Sheet (pgs. 23) 21

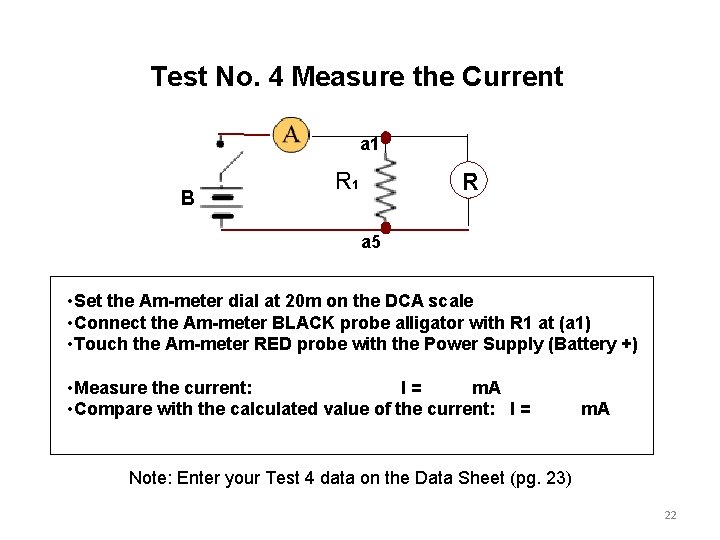
Test No. 4 Measure the Current a 1 B R 1 R a 5 • Set the Am-meter dial at 20 m on the DCA scale • Connect the Am-meter BLACK probe alligator with R 1 at (a 1) • Touch the Am-meter RED probe with the Power Supply (Battery +) • Measure the current: I= m. A • Compare with the calculated value of the current: I = m. A Note: Enter your Test 4 data on the Data Sheet (pg. 23) 22

Student Name: ___________ Experiment No. 3 --- Test Data Sheet with Estimated and Actual Test Results Test No. 1 Four resistors in SERIES Test No. 2 Two resistors in PARALLEL with each other Test No. 3 Measure the current with two resistors in parallel Test No. 4 Measure the current in the circuit with one resistor Expected Actual ____ Ohm _______Ohm ____ m. A _______m. A 1. Explain why is there a difference in voltage between No. 1 and 2 tests? ________________________________________ 2. Explain why is there a difference between the expected and actual current values in Test No. 4? _______________________________________________________________ 3. Explain why is there a difference between No. 3 and No. 4 tests? ____________________________________________________________________ 10/25/2021 23

New Terminology Resistor-------A material that resists the flow of electrical current. Resistivity------A property of a conductor that opposes electric current flow. Conductor------A material through which electricity flows easily. Insulator-------A material that has exceptionally high resistance, such that it essentially stops the flow of electricity. Ohm’s Law-----The relationship between voltage, current, and resistance. In equation form: I =V/R or V=IR. Circuit Diagram----A drawing depicting an arrangement of components. Open Circuit----No current flows. The electrical circuit is incomplete. Closed Circuit------ Current allowed to flow. The circuit is complete. Short Circuit----An unintended closed circuit. SI Units: -------A system of physical units based on the meter, kilogram, second, ampere, kelvin Electric potential-- The capacity of an electric field to do work on an electric charge, to move it between two specified points. The difference between two electric potentials is Voltage, [Volt or V] The reference point is the Earth or Ground. Electric current-----A flow of electrically charged particles. I = q/t, [A] Electric field-----An electric charge produced without movement. (See above the electric field surrounding a positive and negative charge q. An electric field E, is a space radiated by electric single point charge q, and acted upon by an electric force F where E = F/q = kq/r 2. Electric Force----Coulomb’s Law expresses the magnitude of the force between two point charges: F = kq 1 xq 2/r 2 Electric Power-------The rate at which electric energy is transferred by an electric circuit. The unit of electric power is the Watt (W = Vx. A). Electrical Energy--- -A physical quantity that expresses over time the rate at which electric power W is being transmitted Whr. Battery-------- A device that converts stored chemical energy into useful electrical energy. Once an external connection is made between its positive and negative terminals a chemical reaction is initiated that generates electrons at the anode to supply the current of the battery to the external circuit. 24

Summary You learned: -How to calculate resistances in series and parallel circuits -Ohm’s law (I = V/R or its equivalent forms (V = Ix. R and R = V/I) ~If we know two among three variables (voltage, current and resistance), Ohm’s Law allows us to calculate the unknown. -Electric units of measurement: Ohm (resistance), Ampere (current), Volt (voltage), Watt (power) NEW CONCEPT: Power is the rate of doing work. The power dissipated in a resistor is the product of voltage and current. P = VI = V 2/R = I 2 R 25

Resistor Types 26

Breadboard Solid lines are impregnated with flat conducting stripped copper wires. Wire inserted in a front view hole makes contact with one of the copper wires in the back. A breadboard is a piece of a plastic board perforated with small holes and conduction channels that allow electronic parts to be mounted and connected into circuits. 27

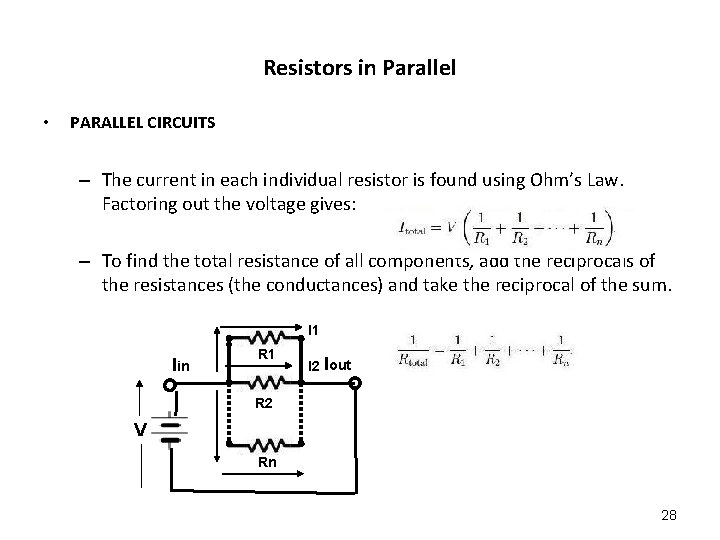
Resistors in Parallel • PARALLEL CIRCUITS – The current in each individual resistor is found using Ohm’s Law. Factoring out the voltage gives: – To find the total resistance of all components, add the reciprocals of the resistances (the conductances) and take the reciprocal of the sum. I 1 Iin R 1 I 2 Iout R 2 V Rn 28