Experiment 5 Stackelberg competition a What kind of

Experiment 5 § Stackelberg competition a) What kind of game is this: sequential or simultaneous? What is the best approach to solve the game? b) Try to find the Nash equilibrium of the game using the payoff table provided in the instructions. Take into account the order of play. Which quantity should the first mover announce? Which quantity should the second mover choose? Is this the only Nash equilibrium in this game? Can you derive the Nash equilibrium mathematically? © WU IMS 1

Experiment 5 § Again, we have a player who moves before the other player. § Thus, the second mover will condition her behavior on whatever the first mover does. § Specifically, the second mover will choose her best response given the choice of the first mover she observes. © WU IMS 2
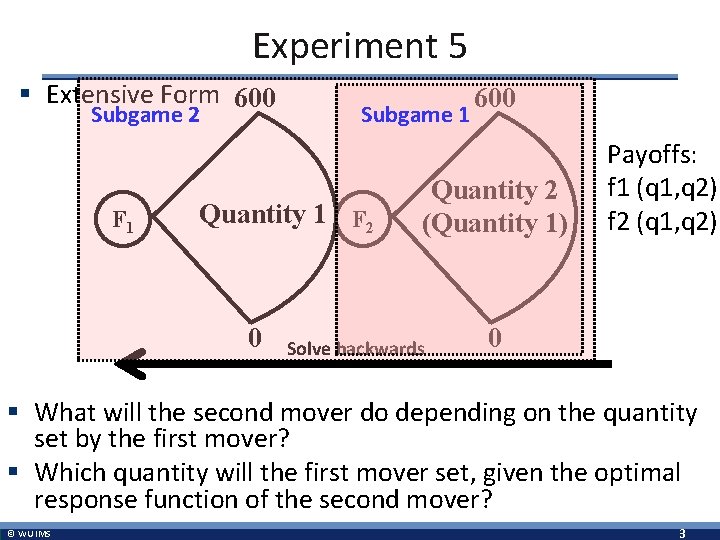
Experiment 5 § Extensive Form 600 Subgame 2 F 1 Subgame 1 Quantity 1 F 2 0 600 Quantity 2 (Quantity 1) Solve backwards Payoffs: f 1 (q 1, q 2) f 2 (q 1, q 2) 0 § What will the second mover do depending on the quantity set by the first mover? § Which quantity will the first mover set, given the optimal response function of the second mover? © WU IMS 3
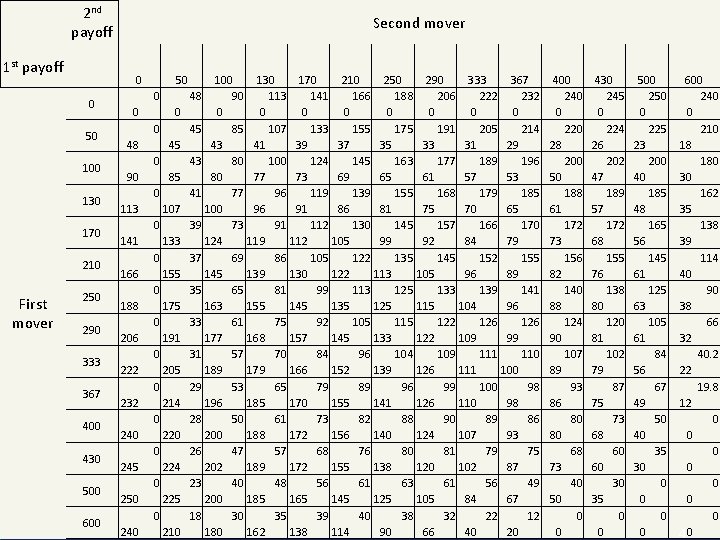
2 nd payoff 1 st payoff 0 50 100 130 170 210 250 290 333 367 400 430 500 © WU IMS Experiment 5 0 First mover Second mover 600 50 0 0 0 0 48 45 0 90 113 141 166 188 206 222 232 240 245 250 240 85 0 107 0 133 0 155 0 175 0 191 0 205 0 214 0 220 0 224 0 225 0 210 100 130 170 210 250 290 333 367 48 90 113 141 166 188 206 222 232 0 0 0 0 45 85 107 133 155 175 191 205 214 43 41 39 37 35 33 31 29 43 80 100 124 145 163 177 189 196 80 77 73 69 65 61 57 53 41 77 96 119 139 155 168 179 185 100 96 91 86 81 75 70 65 39 73 91 112 130 145 157 166 170 124 119 112 105 99 92 84 79 37 69 86 105 122 135 145 152 155 145 139 130 122 113 105 96 89 35 65 81 99 113 125 133 139 141 163 155 145 135 125 115 104 96 33 61 75 92 105 115 122 126 177 168 157 145 133 122 109 99 31 57 70 84 96 104 109 111 110 189 179 166 152 139 126 111 100 29 53 65 79 89 96 99 100 98 196 185 170 155 141 126 110 98 28 50 61 73 82 88 90 89 86 200 188 172 156 140 124 107 93 26 47 57 68 76 80 81 79 75 202 189 172 155 138 120 102 87 23 40 48 56 61 63 61 56 49 200 185 165 145 125 105 84 67 18 30 35 39 40 38 32 22 12 180 162 138 114 90 66 40 20 400 240 0 220 28 200 50 188 61 172 73 156 82 140 88 124 90 107 89 93 86 80 80 68 73 40 50 0 0 430 245 0 224 26 202 47 189 57 172 68 155 76 138 80 120 81 102 79 87 75 73 68 60 60 30 35 0 0 500 250 0 225 23 200 40 185 48 165 56 145 61 125 63 105 61 84 56 67 49 50 40 35 30 0 0 600 240 0 210 18 180 30 162 35 138 39 114 40 90 38 66 32 40. 2 22 19. 8 12 0 0 0 0 40
2 nd payoff 1 st payoff 0 50 100 130 170 210 250 290 333 367 400 430 500 © WU IMS Experiment 5 0 First mover Second mover 600 50 0 0 0 0 48 45 113 141 166 188 206 222 232 240 245 250 240 400 240 0 220 28 200 50 188 61 172 73 156 82 140 88 124 90 107 89 93 86 80 80 68 73 40 50 0 0 430 245 0 224 26 202 47 189 57 172 68 155 76 138 80 120 81 102 79 87 75 73 68 60 60 30 35 0 0 T O N S F I O S I M H T R O F L. E A M M A R G O L N A THE QUENTI E S E TH 0 90 100 130 170 210 250 290 333 367 48 90 113 141 166 188 206 222 232 0 0 0 0 45 85 107 133 155 175 191 205 214 43 41 39 37 35 33 31 29 43 80 100 124 145 163 177 189 196 80 77 73 69 65 61 57 53 41 77 96 119 139 155 168 179 185 100 96 91 86 81 75 70 65 39 73 91 112 130 145 157 166 170 124 119 112 105 99 92 84 79 37 69 86 105 122 135 145 152 155 145 139 130 122 113 105 96 89 35 65 81 99 113 125 133 139 141 163 155 145 135 125 115 104 96 33 61 75 92 105 115 122 126 177 168 157 145 133 122 109 99 31 57 70 84 96 104 109 111 110 189 179 166 152 139 126 111 100 29 53 65 79 89 96 99 100 98 196 185 170 155 141 126 110 98 28 50 61 73 82 88 90 89 86 200 188 172 156 140 124 107 93 26 47 57 68 76 80 81 79 75 202 189 172 155 138 120 102 87 23 40 48 56 61 63 61 56 49 200 185 165 145 125 105 84 67 18 30 35 39 40 38 32 22 12 180 162 138 114 90 66 40 20 85 0 107 0 133 0 155 0 175 0 191 0 205 0 214 0 220 0 224 0 225 0 210 500 250 0 225 23 200 40 185 48 165 56 145 61 125 63 105 61 84 56 67 49 50 40 35 30 0 0 600 240 0 210 18 180 30 162 35 138 39 114 40 90 38 66 32 40. 2 22 19. 8 12 0 0 0 0 50
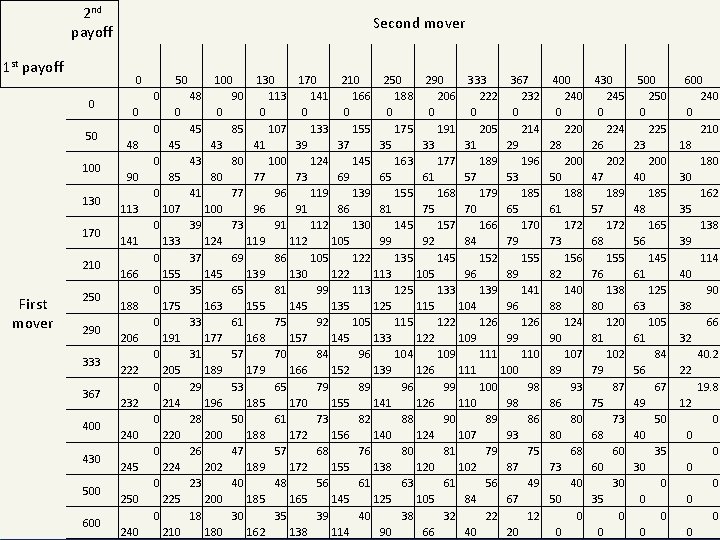
2 nd payoff 1 st payoff 0 50 100 130 170 210 250 290 333 367 400 430 500 © WU IMS Experiment 5 0 First mover Second mover 600 50 0 0 0 0 48 45 0 90 113 141 166 188 206 222 232 240 245 250 240 85 0 107 0 133 0 155 0 175 0 191 0 205 0 214 0 220 0 224 0 225 0 210 100 130 170 210 250 290 333 367 48 90 113 141 166 188 206 222 232 0 0 0 0 45 85 107 133 155 175 191 205 214 43 41 39 37 35 33 31 29 43 80 100 124 145 163 177 189 196 80 77 73 69 65 61 57 53 41 77 96 119 139 155 168 179 185 100 96 91 86 81 75 70 65 39 73 91 112 130 145 157 166 170 124 119 112 105 99 92 84 79 37 69 86 105 122 135 145 152 155 145 139 130 122 113 105 96 89 35 65 81 99 113 125 133 139 141 163 155 145 135 125 115 104 96 33 61 75 92 105 115 122 126 177 168 157 145 133 122 109 99 31 57 70 84 96 104 109 111 110 189 179 166 152 139 126 111 100 29 53 65 79 89 96 99 100 98 196 185 170 155 141 126 110 98 28 50 61 73 82 88 90 89 86 200 188 172 156 140 124 107 93 26 47 57 68 76 80 81 79 75 202 189 172 155 138 120 102 87 23 40 48 56 61 63 61 56 49 200 185 165 145 125 105 84 67 18 30 35 39 40 38 32 22 12 180 162 138 114 90 66 40 20 400 240 0 220 28 200 50 188 61 172 73 156 82 140 88 124 90 107 89 93 86 80 80 68 73 40 50 0 0 430 245 0 224 26 202 47 189 57 172 68 155 76 138 80 120 81 102 79 87 75 73 68 60 60 30 35 0 0 500 250 0 225 23 200 40 185 48 165 56 145 61 125 63 105 61 84 56 67 49 50 40 35 30 0 0 600 240 0 210 18 180 30 162 35 138 39 114 40 90 38 66 32 40. 2 22 19. 8 12 0 0 0 0 60
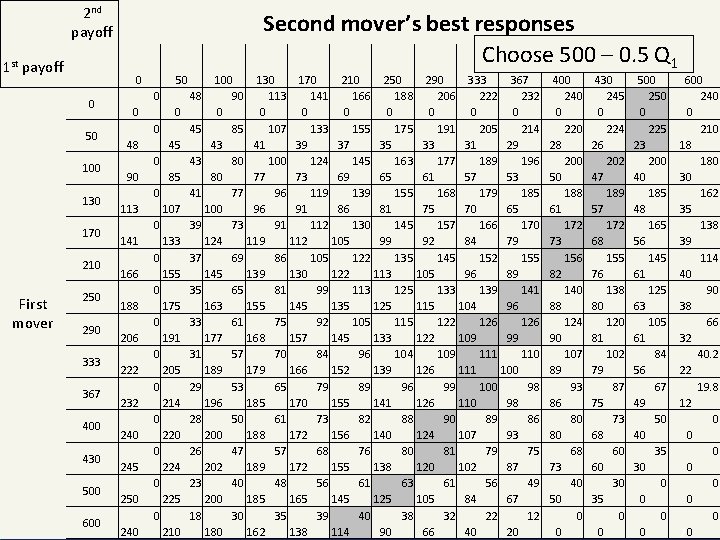
2 nd payoff 1 st payoff 0 50 100 130 170 210 250 290 333 367 400 430 500 © WU IMS Experiment 5 0 First mover Second mover’s best responses Choose 500 – 0. 5 Q 1 600 50 0 0 0 0 48 45 0 90 113 141 166 188 206 222 232 240 245 250 240 85 0 107 0 133 0 155 0 175 0 191 0 205 0 214 0 220 0 224 0 225 0 210 100 130 170 210 250 290 333 367 48 90 113 141 166 188 206 222 232 0 0 0 0 45 85 107 133 155 175 191 205 214 43 41 39 37 35 33 31 29 43 80 100 124 145 163 177 189 196 80 77 73 69 65 61 57 53 41 77 96 119 139 155 168 179 185 100 96 91 86 81 75 70 65 39 73 91 112 130 145 157 166 170 124 119 112 105 99 92 84 79 37 69 86 105 122 135 145 152 155 145 139 130 122 113 105 96 89 35 65 81 99 113 125 133 139 141 163 155 145 135 125 115 104 96 33 61 75 92 105 115 122 126 177 168 157 145 133 122 109 99 31 57 70 84 96 104 109 111 110 189 179 166 152 139 126 111 100 29 53 65 79 89 96 99 100 98 196 185 170 155 141 126 110 98 28 50 61 73 82 88 90 89 86 200 188 172 156 140 124 107 93 26 47 57 68 76 80 81 79 75 202 189 172 155 138 120 102 87 23 40 48 56 61 63 61 56 49 200 185 165 145 125 105 84 67 18 30 35 39 40 38 32 22 12 180 162 138 114 90 66 40 20 400 240 0 220 28 200 50 188 61 172 73 156 82 140 88 124 90 107 89 93 86 80 80 68 73 40 50 0 0 430 245 0 224 26 202 47 189 57 172 68 155 76 138 80 120 81 102 79 87 75 73 68 60 60 30 35 0 0 500 250 0 225 23 200 40 185 48 165 56 145 61 125 63 105 61 84 56 67 49 50 40 35 30 0 0 600 240 0 210 18 180 30 162 35 138 39 114 40 90 38 66 32 40. 2 22 19. 8 12 0 0 0 0 70

Experiment 5 § Now, • anticipating that the second mover will play a best response, • the first mover can just choose the strategy which gives him the best payoff given that best response. © WU IMS 8
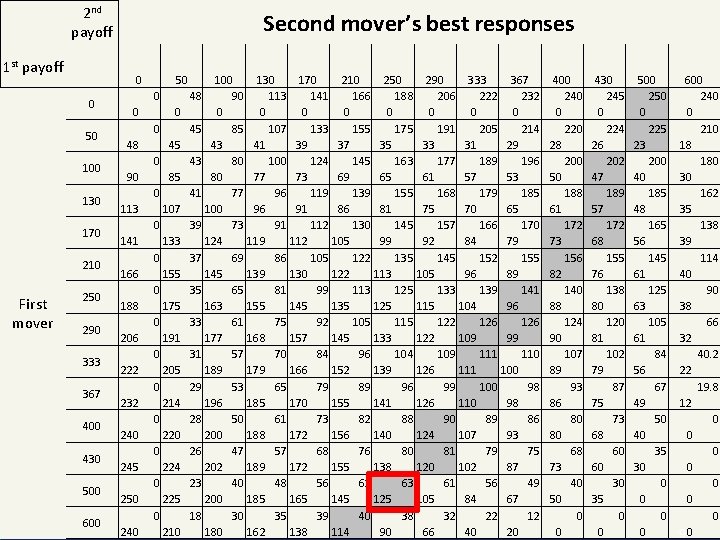
2 nd payoff 1 st payoff 0 50 100 130 170 210 250 290 333 367 400 430 500 © WU IMS Experiment 5 0 First mover Second mover’s best responses 600 50 0 0 0 0 48 45 0 90 113 141 166 188 206 222 232 240 245 250 240 85 0 107 0 133 0 155 0 175 0 191 0 205 0 214 0 220 0 224 0 225 0 210 100 130 170 210 250 290 333 367 48 90 113 141 166 188 206 222 232 0 0 0 0 45 85 107 133 155 175 191 205 214 43 41 39 37 35 33 31 29 43 80 100 124 145 163 177 189 196 80 77 73 69 65 61 57 53 41 77 96 119 139 155 168 179 185 100 96 91 86 81 75 70 65 39 73 91 112 130 145 157 166 170 124 119 112 105 99 92 84 79 37 69 86 105 122 135 145 152 155 145 139 130 122 113 105 96 89 35 65 81 99 113 125 133 139 141 163 155 145 135 125 115 104 96 33 61 75 92 105 115 122 126 177 168 157 145 133 122 109 99 31 57 70 84 96 104 109 111 110 189 179 166 152 139 126 111 100 29 53 65 79 89 96 99 100 98 196 185 170 155 141 126 110 98 28 50 61 73 82 88 90 89 86 200 188 172 156 140 124 107 93 26 47 57 68 76 80 81 79 75 202 189 172 155 138 120 102 87 23 40 48 56 61 63 61 56 49 200 185 165 145 125 105 84 67 18 30 35 39 40 38 32 22 12 180 162 138 114 90 66 40 20 400 240 0 220 28 200 50 188 61 172 73 156 82 140 88 124 90 107 89 93 86 80 80 68 73 40 50 0 0 430 245 0 224 26 202 47 189 57 172 68 155 76 138 80 120 81 102 79 87 75 73 68 60 60 30 35 0 0 500 250 0 225 23 200 40 185 48 165 56 145 61 125 63 105 61 84 56 67 49 50 40 35 30 0 0 600 240 0 210 18 180 30 162 35 138 39 114 40 90 38 66 32 40. 2 22 19. 8 12 0 0 0 0 90

Experiment 5 § So the (subgame perfect) Nash Equilibrium which we found by rollback is: • Producer 1: Choose 500. • Producer 2: Choose 500 – 0. 5 Q 1. © WU IMS 10

Experiment 5 § In math: • 2 nd movers profit 2 = P * Q 2 = (1 -0. 001(Q 1+Q 2)) Q 2 • max 2 0 = 1 - 0. 001 Q 1 - 0. 002 Q 2* • Q 2* = 500 – 0. 5 Q 1 (best reply function) • 1 st movers profit 1 = P * Q 1 = (1 -0. 001(Q 1+Q 2)) Q 1 • First mover can count on 2 nd movers best response • 1 = P * Q 1 = (1 -0. 001(Q 1+(500 – 0. 5 Q 1 ))) Q 1 = 0. 5 Q 1 -0. 0005 Q 1 Q 1 • max 1 0 = 0. 5 - 0. 001 Q 1* • Q 1* = 500 Q 2* = 500 – 0. 5 Q 1* = 250 § First mover chooses higher quantity than second mover and makes more profit © WU IMS 11

Experiment 5 § There are many other (not subgame perfect) NEs. § Assume the following strategies: • 2 nd mover: choose “ 430” if 1 st mover plays “ 100”, and “ 600” otherwise. • 1 st mover: choose “ 100”. § Playing “ 100” is the best answer of the 1 st mover to the 2 nd mover’s strategy. § Playing the 2 nd mover’s strategy is one of the best responses of the 2 nd mover if the 1 st mover plays “ 100”. § So we have a Nash equilibrium, but it is not subgame perfect. The “ 600 otherwise” part of the 2 nd mover’s strategy is not credible. The 2 nd mover should not do that when the 1 st mover chooses something else than ” 100”. So the 1 st mover should not believe it. © WU IMS 12

Experiment 5 § Note, however, that while this is the only subgame perfect equilibrium in this game, there are many other (not subgame perfect) Nash equilibria. § Assume, for example, that the 2 nd mover plays the strategy “ 430” if 1 st mover plays “ 100”, and “ 600” otherwise. • Playing “ 100” is the best answer of the 1 st mover to this strategy. • Playing this strategy is one of the best responses of the 2 nd mover conditional that the 1 st mover plays “ 100”. • This constitutes a Nash equilibrium, but it is not subgame perfect. • The “ 600 otherwise” is not credible. The 2 nd mover should not do that when he is at play. So the 1 st mover should not believe it. © WU IMS 13
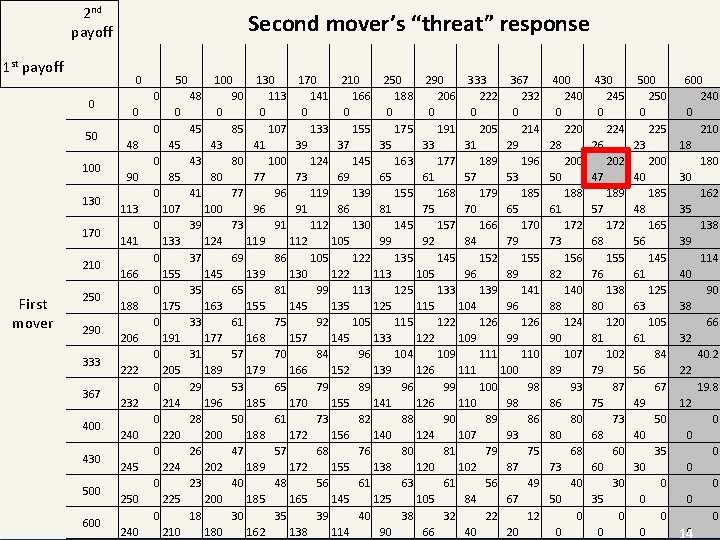
2 nd payoff 1 st payoff 0 50 100 130 170 210 250 290 333 367 400 430 500 © WU IMS Experiment 5 0 First mover Second mover’s “threat” response 600 50 0 0 0 0 48 45 0 90 113 141 166 188 206 222 232 240 245 250 240 85 0 107 0 133 0 155 0 175 0 191 0 205 0 214 0 220 0 224 0 225 0 210 100 130 170 210 250 290 333 367 48 90 113 141 166 188 206 222 232 0 0 0 0 45 85 107 133 155 175 191 205 214 43 41 39 37 35 33 31 29 43 80 100 124 145 163 177 189 196 80 77 73 69 65 61 57 53 41 77 96 119 139 155 168 179 185 100 96 91 86 81 75 70 65 39 73 91 112 130 145 157 166 170 124 119 112 105 99 92 84 79 37 69 86 105 122 135 145 152 155 145 139 130 122 113 105 96 89 35 65 81 99 113 125 133 139 141 163 155 145 135 125 115 104 96 33 61 75 92 105 115 122 126 177 168 157 145 133 122 109 99 31 57 70 84 96 104 109 111 110 189 179 166 152 139 126 111 100 29 53 65 79 89 96 99 100 98 196 185 170 155 141 126 110 98 28 50 61 73 82 88 90 89 86 200 188 172 156 140 124 107 93 26 47 57 68 76 80 81 79 75 202 189 172 155 138 120 102 87 23 40 48 56 61 63 61 56 49 200 185 165 145 125 105 84 67 18 30 35 39 40 38 32 22 12 180 162 138 114 90 66 40 20 400 240 0 220 28 200 50 188 61 172 73 156 82 140 88 124 90 107 89 93 86 80 80 68 73 40 50 0 0 430 245 0 224 26 202 47 189 57 172 68 155 76 138 80 120 81 102 79 87 75 73 68 60 60 30 35 0 0 500 250 0 225 23 200 40 185 48 165 56 145 61 125 63 105 61 84 56 67 49 50 40 35 30 0 0 600 240 0 210 18 180 30 162 35 138 39 114 40 90 38 66 32 40. 2 22 19. 8 12 0 0 0 0 140

Experiment 5 § Data c) Analyze the data set of experiment 5. What can you tell about the behavior of participants? Do they behave as your analysis above suggested? Is there a change in behavior over time, in the different rounds of the markets? © WU IMS 15
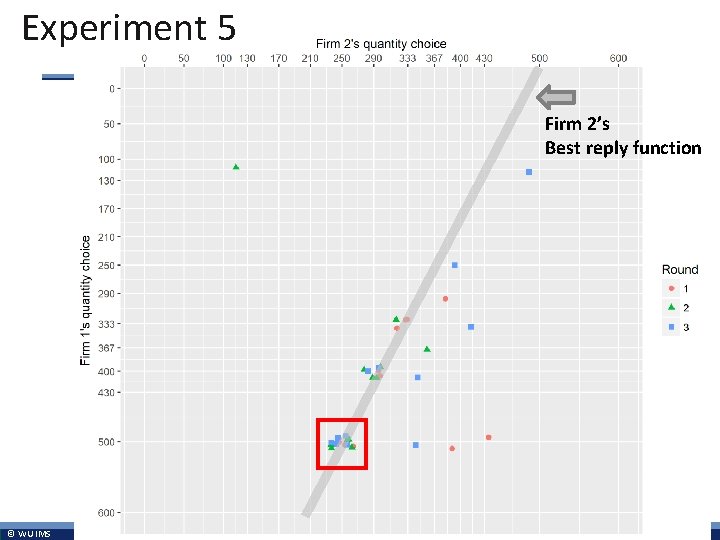
Experiment 5 Firm 2’s Best reply function © WU IMS 16
- Slides: 16