Experiment 11 2 Proposer Ultimatum Game a What








- Slides: 14

Experiment 11 § 2 -Proposer Ultimatum Game a) What kind of game is this: sequential or simultaneous? b) Find all subgame perfect NEs of the single round game. Hints: • Assume that person C is indifferent if both offers are exactly the same, and will choose randomly between both offers in this case. • Use rollback. That is, first solve for person C’s optimal strategy given what A and B have done. • Then, inspect the resulting 2 -player game between players A and B, assuming an optimal reaction by player C. Solve using a normal form version of the game (use 0. 01, 1, 2, 3, 4, 5, 6, 7, 8 as possible choices for A and B). © WU IMS 1

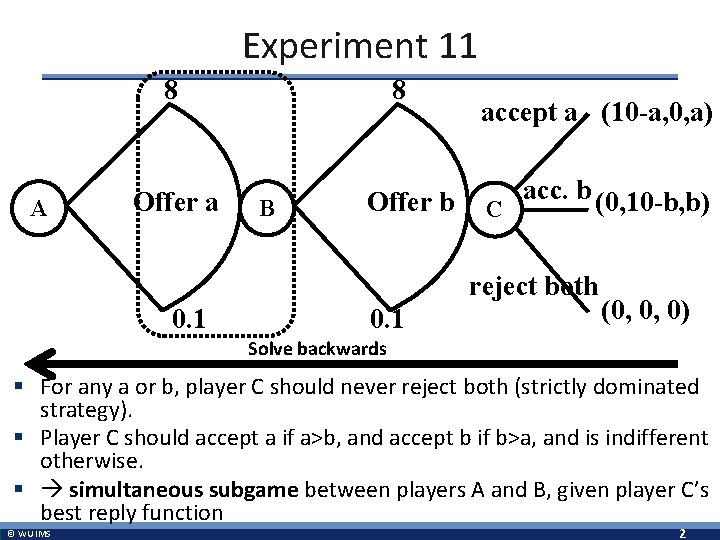
Experiment 11 8 A Offer a 8 B Offer b accept a (10 -a, 0, a) C acc. b (0, 10 -b, b) reject both 0. 1 (0, 0, 0) Solve backwards § For any a or b, player C should never reject both (strictly dominated strategy). § Player C should accept a if a>b, and accept b if b>a, and is indifferent otherwise. § simultaneous subgame between players A and B, given player C’s best reply function © WU IMS 2

Experiment 11 § This is a mixed sequential/simultaneous game. • Players A and B decide simultaneously. • Player C decides thereafter. § Rollback: start with player C. • If interested in money, Player C should accept the proposal which offers her more money. • She is indifferent when both offers are the same. § Players A and B face a simultaneous game. © WU IMS 3

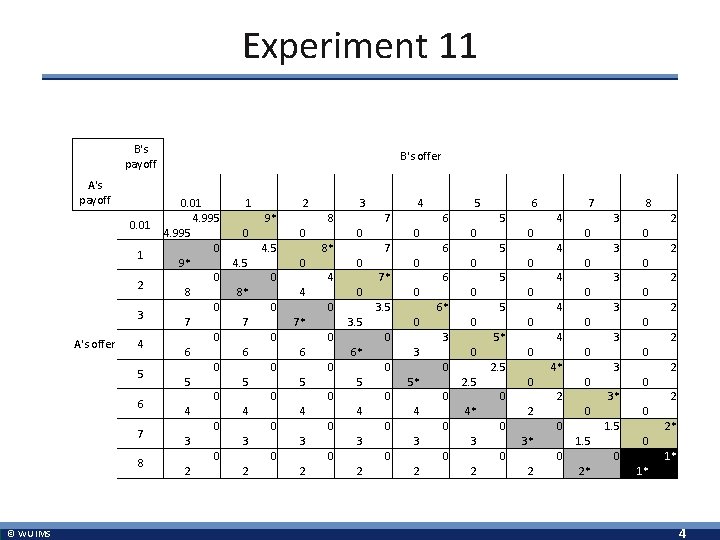
Experiment 11 B's payoff A's payoff 0. 01 1 2 3 A's offer 4 5 6 7 8 © WU IMS B's offer 0. 01 1 4. 995 9* 4. 995 0 0 4. 5 9* 4. 5 0 0 8 8* 0 0 7 7 0 0 6 6 0 0 5 5 0 0 4 4 0 0 3 3 0 0 2 2 2 3 8 0 7 0 8* 0 0 0 4 7* 0 0 0 5 0 4 0 0 3 0 2 3* 2 0 1. 5 0 2 2 0 0 0 0 2 0 3 2 0 0 3 0 2 2 0 0 4* 0 0 0 2 3 4 2. 5 0 0 0 2. 5 4 0 0 5* 2 3 4 0 0 5* 4 3 3 0 0 0 2 3 4 5 0 3 0 0 0 8 3 4 5 6* 0 0 0 7 4 5 6 3. 5 6 0 0 0 6 5 6 7* 0 5 6 7 4 2 4 2* 0 0 2* 1* 1* 4

Experiment 11 § The subgame perfect Nash equilibrium of the game is: • Player A: Offer a price of 8. • Player B: Offer a price of 8. • Player C: Accept A’s offer if a>b, accept B’s offer if b>a, and choose randomly otherwise. © WU IMS 5

Experiment 11: More formally § Assume the following rules: a is the offer of A to C, and b is the offer of B to C, with 0 < a, b <= 8. § Then A and B have the following payoff functions in the subgame between A and B (given C’s optimal response): © WU IMS • A: A = 0 0. 5(10 -a) 10 -a if a<b if a=b if a>b • B: B = 0 0. 5(10 -b) 10 -b if a>b if a=b if a<b 6

Experiment 11: More formally § Then, the best reply functions of players A and B (for any b/a) are: • A: a*(b)= 8 if b=8 b+0. 01 if b<8 8 if a=8 • B: b*(a)= a+0. 01 if a<8 § Thus, we can write a*(b) as a*(b*(a*)): 8 if a*= 8 • A: a*= 8 if a*= 7. 99 (a*+0. 01)+0. 01 if a*+0. 01<8 § The only solution for a* is a*=8. Thus, b*= 8. © WU IMS 7

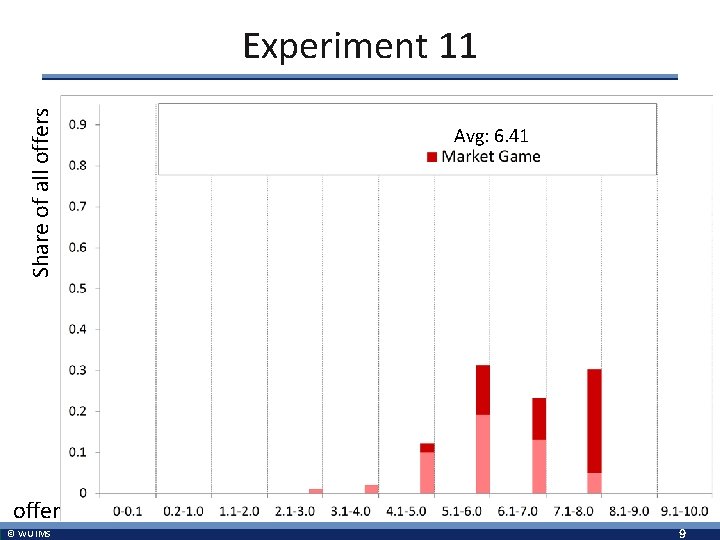
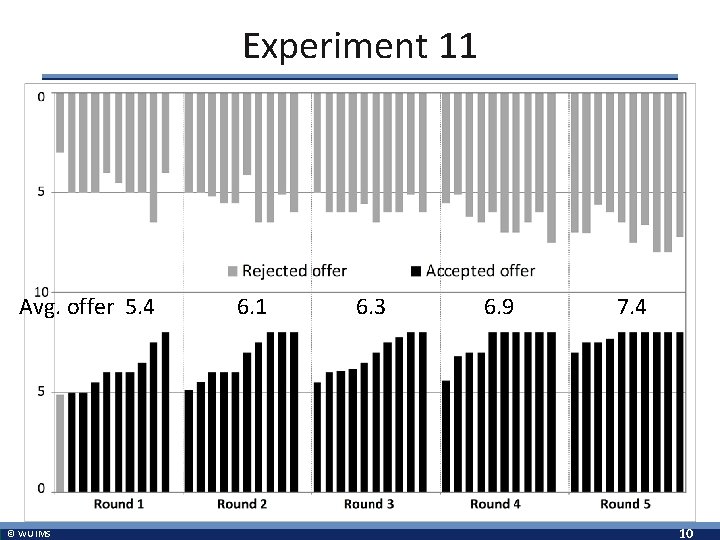
Experiment 11 § Data c) Analyze the data set of experiment 11 and compare behavior in the experiment to your equilibrium analysis above. Is there a change in behavior over time? d) Compare theoretical predictions and behavior between experiment 11 and experiments 9/10. What do you think drives the differences? © WU IMS 8

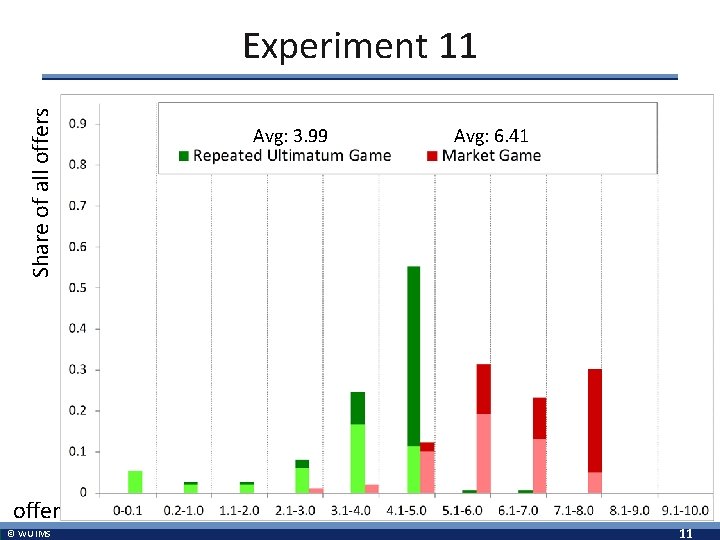
Share of all offers Experiment 11 Avg: 6. 41 offer © WU IMS 9

Experiment 11 Avg. offer 5. 4 6. 1 © WU IMS 6. 3 6. 9 7. 4 10

Share of all offers Experiment 11 Avg: 3. 99 Avg: 6. 41 offer © WU IMS 11

Experiment 11 § Thus, the competition between proposers turns the game around. Though they have Ultimatum power, they will compete their offers up. § Note: even if players are “fair minded” we will have this result. The distribution is unfair anyway (at least one gets nothing), so it’s better if it’s to my advantage than to my disadvantage. § In the Ultimatum game, both proposer and responder are “monopolists”. Without any of them, there are no gains to realize. § In this game, proposers are exchangeable. The responder alone is a monopolist. § In a negotiation between rational players, you can only get in value what makes you distinct from your next replacement. © WU IMS 12

Experiment 11 § Compare to: • Markets: profit of seller = lowest costs among sellers who are not able to trade, minus own costs • Markets: profit of buyer = own value minus highest value among buyers who do not trade • Auctions: profit of auction winner = own value of good minus price (price = highest value among bidders who are not successful – that’s where they stop bidding) • Coalitions: share of pie = Shapley value = value the coalition member brings in compared to an alternative coalition which excludes that member § You are “priced” at your opportunity costs – the value of the next best alternative foregone as the result of making the decision to deal with you © WU IMS 13

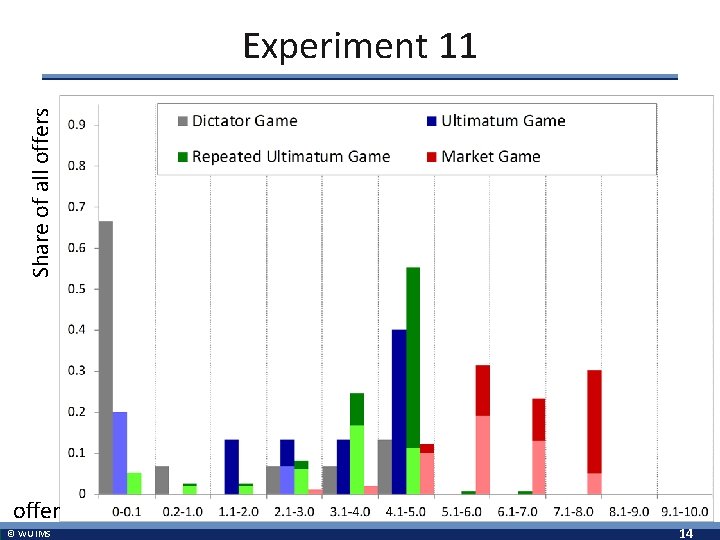
Share of all offers Experiment 11 offer © WU IMS 14