Expected Present value project A YEAR Income Probability

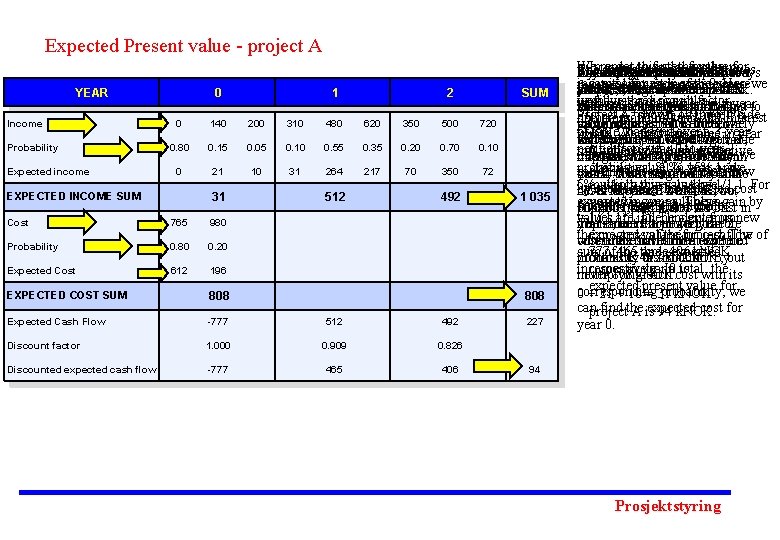
Expected Present value - project A YEAR Income Probability Expected income 0 1 2 SUM 0 140 200 310 480 620 350 500 720 0. 80 0. 15 0. 05 0. 10 0. 55 0. 35 0. 20 0. 70 0. 10 0 21 10 31 264 217 70 350 72 EXPECTED INCOME SUM 31 Cost 765 980 Probability 0. 80 0. 20 Expected Cost 612 196 512 492 EXPECTED COST SUM 808 Expected Cash Flow -777 512 492 Discount factor 1. 000 0. 909 0. 826 Discounted expected cash flow -777 465 406 1 035 808 227 We In repeat order to this find step the for value the for corresponding probabilities costs for the entire the 3 The expected income for the For By We adding will each choose year, 612 value income this k. NOK one step concept ofwill and two for 196 cost says In year 0, repeat the project have income capital amount for each in of year the 0. years, Here for these values are shown as year period is 808000 NOK, three-year period is: projects, values that k. NOK, we 1. are Three calculate we Aset get or different up B. a value in thethe expected of table. 808 we an investment of 765000 NOK. we will have use three aoccuring discount possible factor well. with costs only in yearto values k. NOK incomes and for with expected use corresponding them cost. as the This Little uncertainty is connected 31 + 512 + 492 = 1035 k. NOK Project A, shown on the left side outcomes: corresponding 0, 140 to and a 10% 200 interest 0. decision value probabilities is not basis. agive real Therefore, value we this investment. Itus is three 20%forlikely of table, happens over a 3 -year k. NOK. rate. We These find this value are in year When have expected will our expected project, usewe the incomes. expected butvalues if we Altogether, costvalue that the project will have period from 0 torespective year 2. we multiplied 0, where with ityear isas equal their to the incomes and expected costs, of implement this 808 gives k. NOK us the 512 project the k. NOK decision many in in overrun, which means costs probabilities: starting value. 80%, Invalue year 15% 1, and we can find the expected cash flow basis. times, year 1. The average income for year of the 1 0 the could become 980000 5%, multiply which this gives value us three by 1/1, 1. by subtracting expected costs never for equals year 512 0 the becomes k. NOK, butcost. For NOK. Because we have two expected yearthe two, incomes. weor. Once multiply These againinby from expected income. 808000 either 31, 264 NOK. 217 we k. NOK. possible magnitudes for cost values 1/(1, 1*1, 1). This gives from us 2, new implement The same isindependent the done project, for year the year 0, are there are two possible the expected progress values ofform thethe for project. cashflow The of cost where ofthe thethat sum investment of will be outcomes a expected discrete sum 777, of 465 the and 406 expected k. NOK 765 incomes k. NOK is three 492 or 980 k. NOK, probability distribution. Bybut incomes respectively. in year In 0 total, is: the never 808 k. NOK. multiplying each cost with its expected present value for corresponding probability, 0 + 21 + 10 = 31 k. NOK we can find the expected cost for project A is 94 k. NOK. year 0. 94 Prosjektstyring

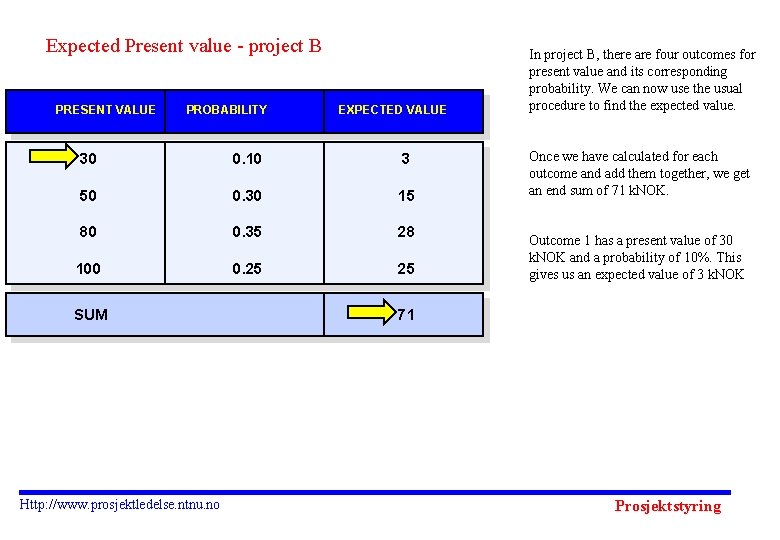
Expected Present value - project B PRESENT VALUE PROBABILITY EXPECTED VALUE 30 0. 10 3 50 0. 30 15 80 0. 35 28 100 0. 25 25 SUM Http: //www. prosjektledelse. ntnu. no In project B, there are four outcomes for present value and its corresponding probability. We can now use the usual procedure to find the expected value. Once we have calculated for each outcome and add them together, we get an end sum of 71 k. NOK. Outcome 1 has a present value of 30 k. NOK and a probability of 10%. This gives us an expected value of 3 k. NOK 71 Prosjektstyring

Project A 94 Project B 71 Http: //www. prosjektledelse. ntnu. no We can now see that project A has the highest expected present value and therefore should be preferred to project B. Both projects have values that do not happen in reality. The amounts that we have calculated only serve for the purpose of comparing the two projects. Prosjektstyring