Expectation Maximization Algorithm Rong Jin A Mixture Model

Expectation Maximization Algorithm Rong Jin

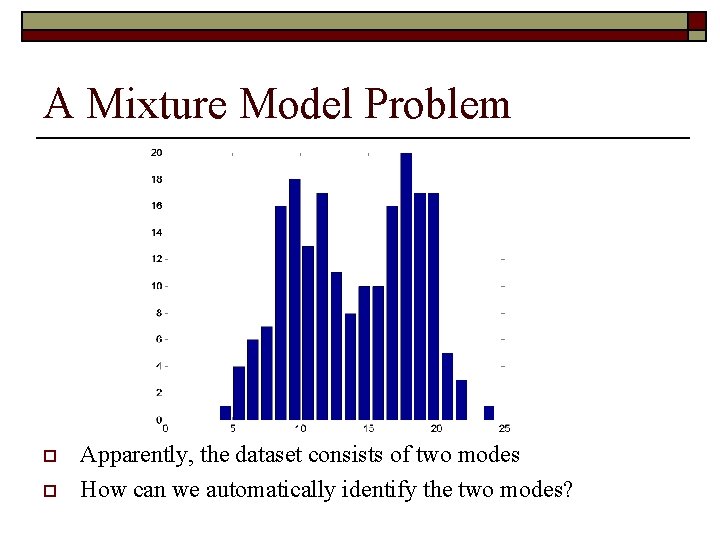
A Mixture Model Problem o o Apparently, the dataset consists of two modes How can we automatically identify the two modes?

Gaussian Mixture Model (GMM) o Assume that the dataset is generated by two mixed Gaussian distributions n n o o Gaussian model 1: Gaussian model 2: If we know the memberships for each bin, estimating the two Gaussian models is easy. How to estimate the two Gaussian models without knowing the memberships of bins?

EM Algorithm for GMM o Let memberships to be hidden variables o EM algorithm for Gaussian mixture model n Unknown memberships: n Unknown Gaussian models: n Learn these two sets of parameters iteratively

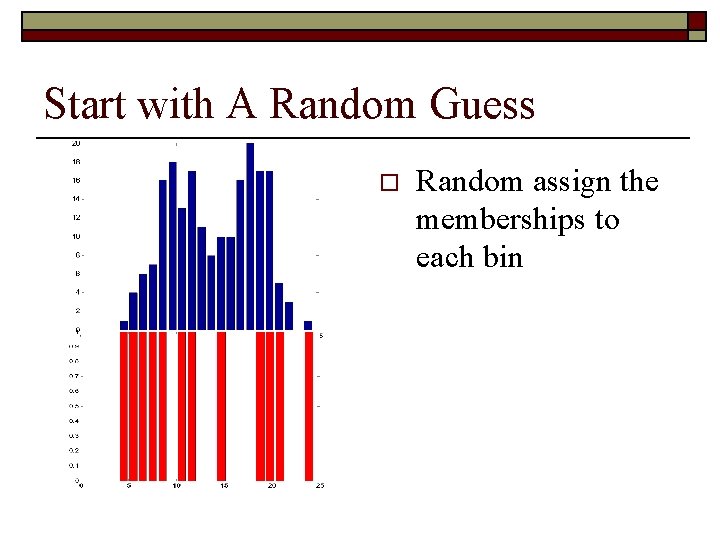
Start with A Random Guess o Random assign the memberships to each bin

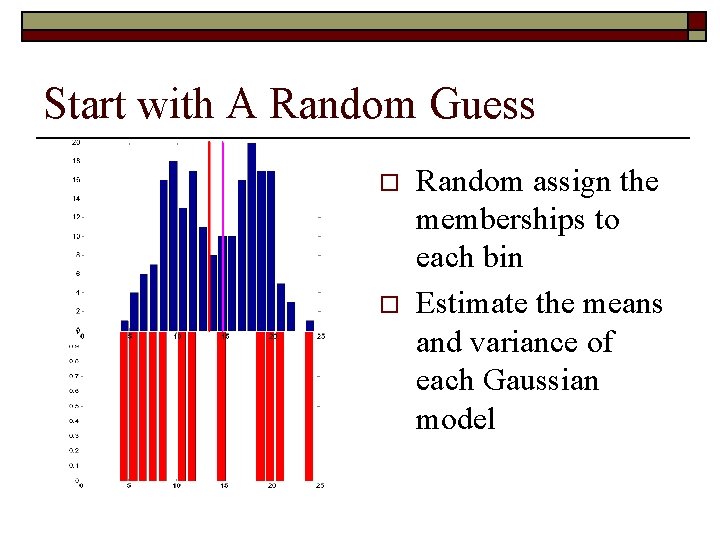
Start with A Random Guess o o Random assign the memberships to each bin Estimate the means and variance of each Gaussian model

E-step o o Fixed the two Gaussian models Estimate the posterior for each data point

EM Algorithm for GMM o Re-estimate the memberships for each bin

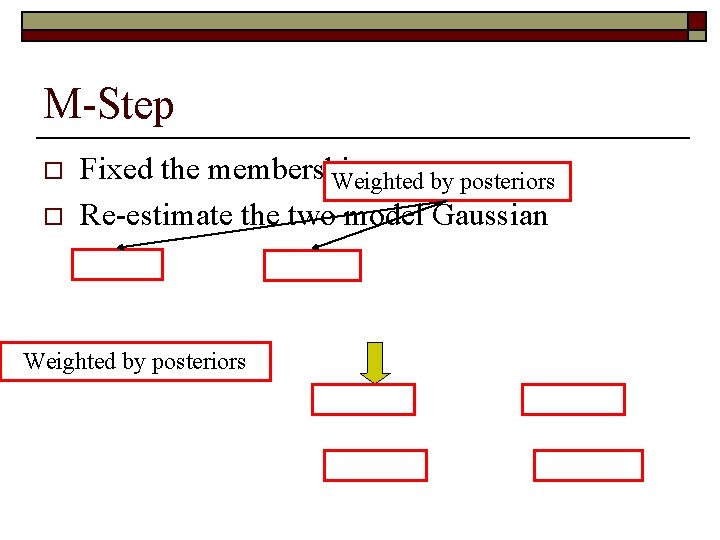
M-Step o o Fixed the memberships Weighted by posteriors Re-estimate the two model Gaussian Weighted by posteriors

EM Algorithm for GMM o o Re-estimate the memberships for each bin Re-estimate the models

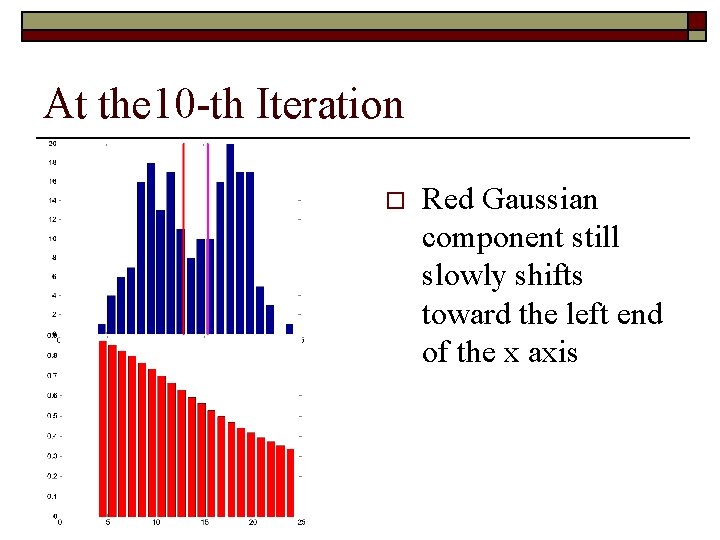
At the 5 -th Iteration o Red Gaussian component slowly shifts toward the left end of the x axis

At the 10 -th Iteration o Red Gaussian component still slowly shifts toward the left end of the x axis

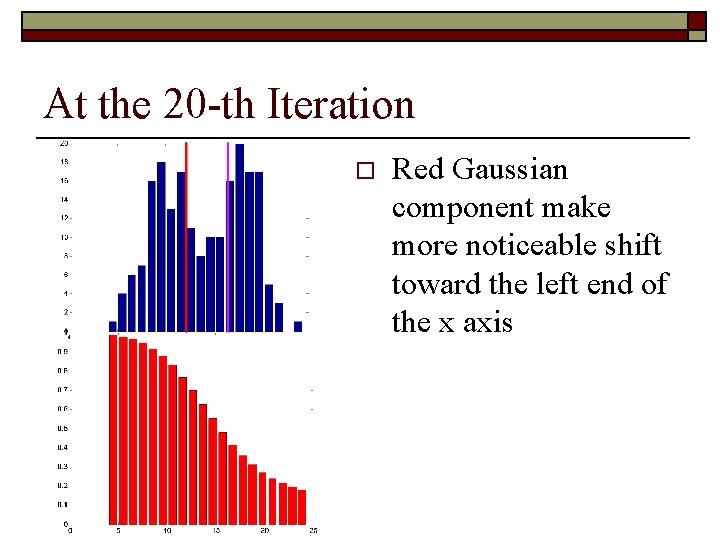
At the 20 -th Iteration o Red Gaussian component make more noticeable shift toward the left end of the x axis

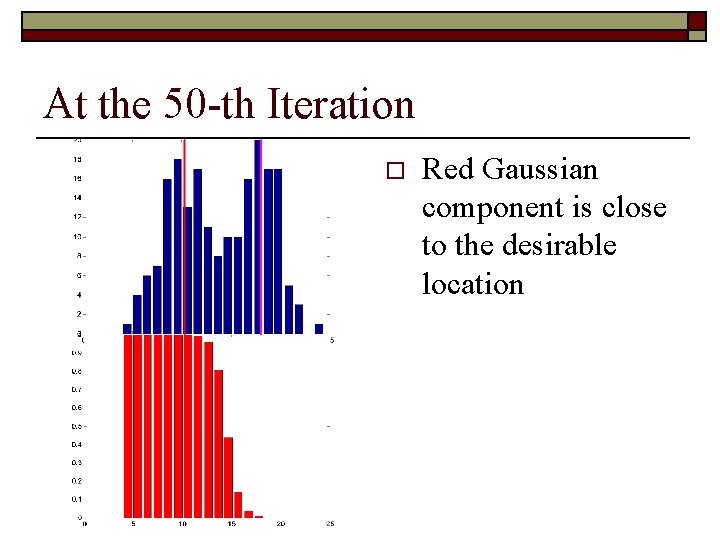
At the 50 -th Iteration o Red Gaussian component is close to the desirable location

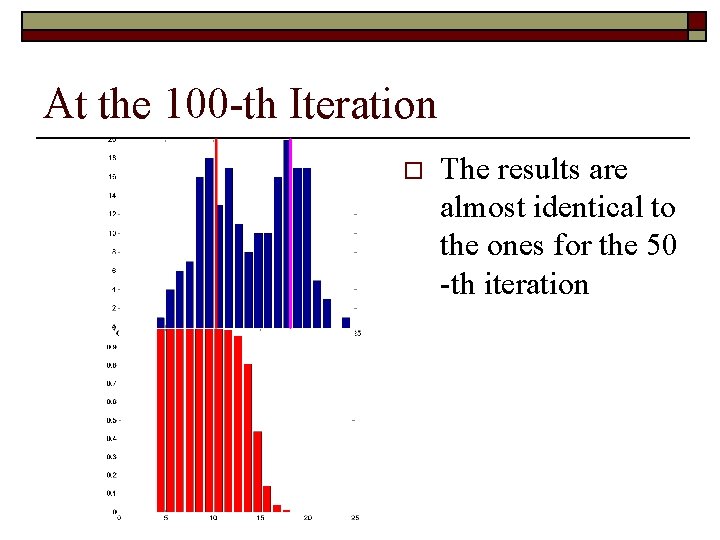
At the 100 -th Iteration o The results are almost identical to the ones for the 50 -th iteration

EM as A Bound Optimization o EM algorithm in fact maximizes the log-likelihood function of training data Likelihood for a data point x o Log-likelihood of training data o

EM as A Bound Optimization o EM algorithm in fact maximizes the log-likelihood function of training data Likelihood for a data point x o Log-likelihood of training data o

EM as A Bound Optimization o EM algorithm in fact maximizes the log-likelihood function of training data Likelihood for a data point x o Log-likelihood of training data o

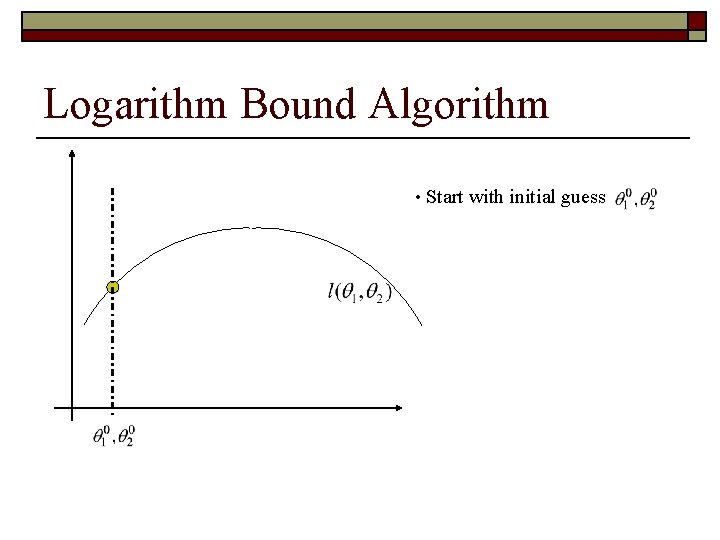
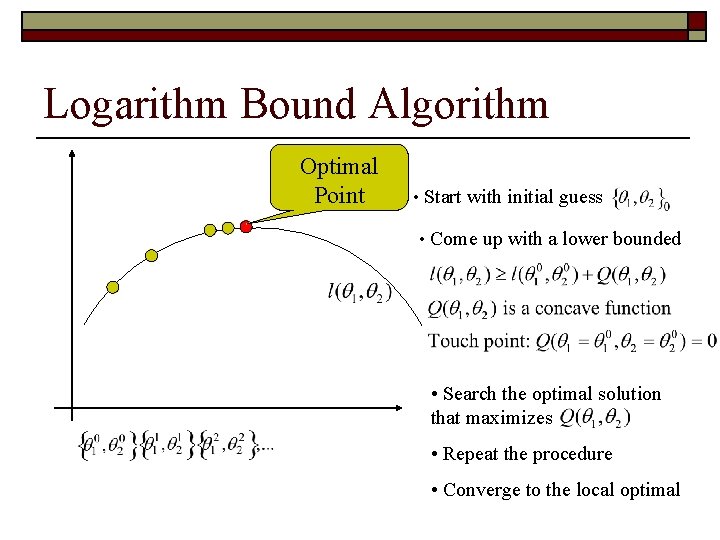
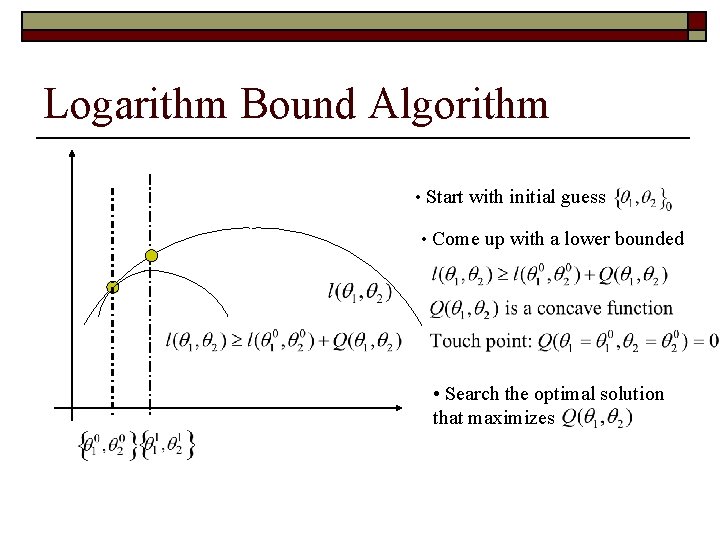
Logarithm Bound Algorithm • Start with initial guess

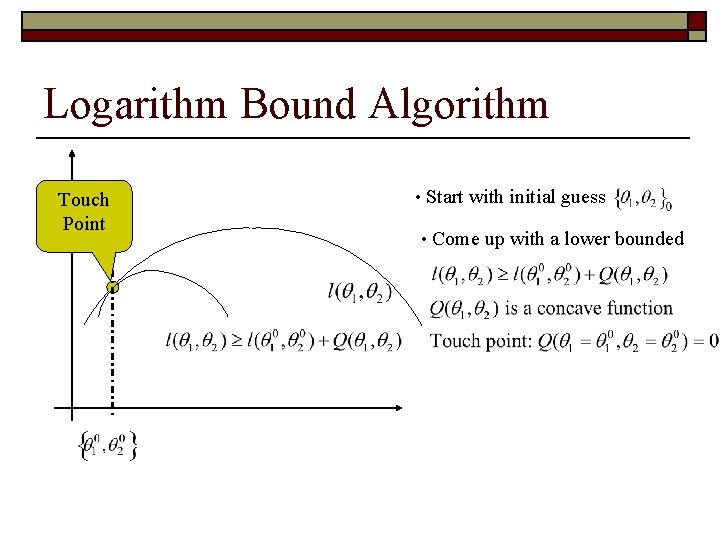
Logarithm Bound Algorithm Touch Point • Start with initial guess • Come up with a lower bounded

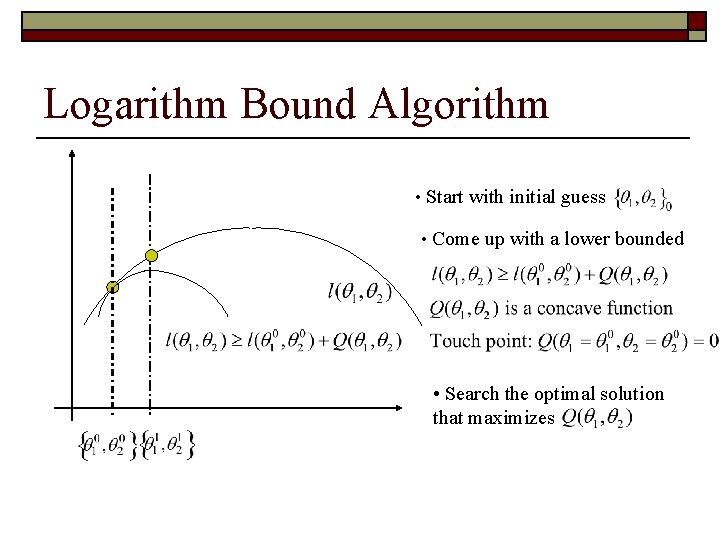
Logarithm Bound Algorithm • Start with initial guess • Come up with a lower bounded • Search the optimal solution that maximizes

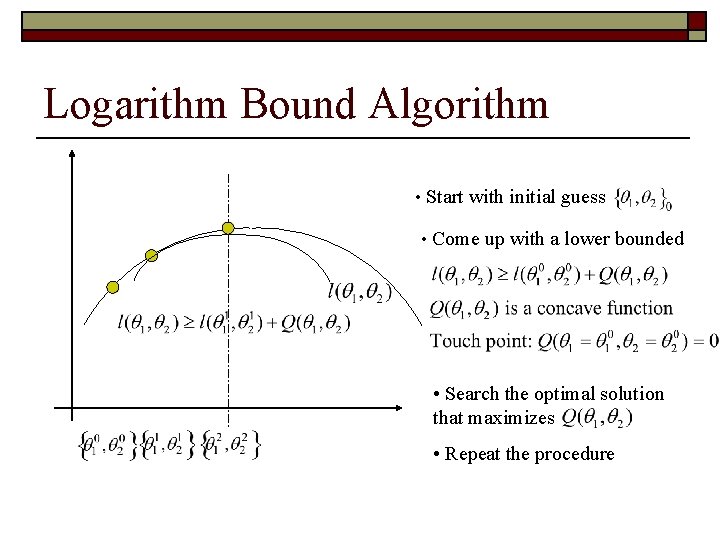
Logarithm Bound Algorithm • Start with initial guess • Come up with a lower bounded • Search the optimal solution that maximizes • Repeat the procedure

Logarithm Bound Algorithm Optimal Point • Start with initial guess • Come up with a lower bounded • Search the optimal solution that maximizes • Repeat the procedure • Converge to the local optimal

EM as A Bound Optimization o o o Parameter for previous iteration: Parameter for current iteration: Compute

Concave property of logarithm function

Definition of posterior

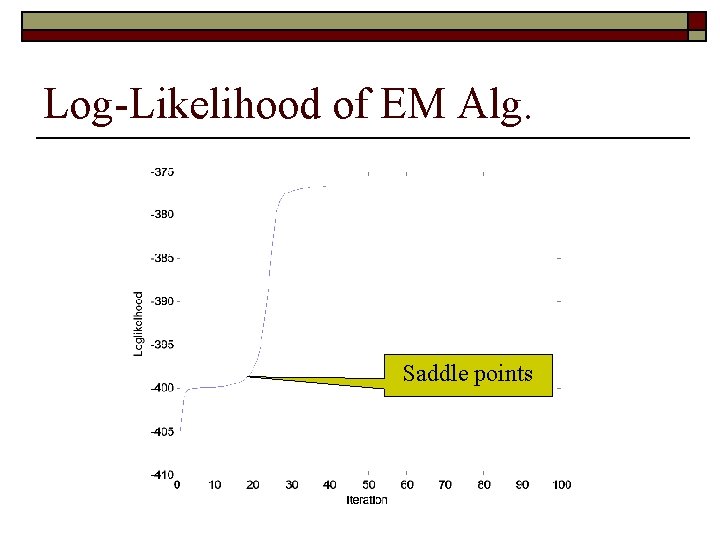
Log-Likelihood of EM Alg. Saddle points

Maximize GMM Model o What is the global optimal solution to GMM? o Maximizing the objective function of GMM is illposed problem

Maximize GMM Model o What is the global optimal solution to GMM? o Maximizing the objective function of GMM is illposed problem

Identify Hidden Variables o o For certain learning problems, identifying hidden variables is not a easy task Consider a simple translation model n For a pair of English and Chinese sentences: n A simple translation model is n The log-likelihood of training corpus

Identify Hidden Variables o Consider a simple case o Alignment variable a(i) o Rewrite

Identify Hidden Variables o Consider a simple case o Alignment variable a(i) o Rewrite

Identify Hidden Variables o Consider a simple case o Alignment variable a(i) o Rewrite

Identify Hidden Variables o Consider a simple case o Alignment variable a(i) o Rewrite

EM Algorithm for A Translation Model o Introduce an alignment variable for each translation pair n o EM algorithm for the translation model n n E-step: compute the posterior for each alignment variable M-step: estimate the translation probability Pr(e|c)

EM Algorithm for A Translation Model o Introduce an alignment variable for each translation pair n o EM algorithm for the translation model n n E-step: compute the posterior for each alignment variable M-step: estimate the translation probability Pr(e|c) We are luck here. In general, this step can be extremely difficult and usually requires approximate approaches

Compute Pr(e|c) o First compute

Compute Pr(e|c) o First compute

Bound Optimization for A Translation Model

Bound Optimization for A Translation Model

Iterative Scaling Maximum entropy model o o Iterative scaling o o All features Sum of features are constant

Iterative Scaling o Compute the empirical mean for each feature of every class, i. e. , for every j and every class y o Start w 1 , w 2 …, wc = 0 Repeat o n n Compute p(y|x) for each training data point (xi, yi) using w from the previous iteration Compute the mean of each feature of every class using the estimated probabilities, i. e. , for every j and every y n Compute n Update w as for every j and every y

Iterative Scaling

Iterative Scaling Can we use the concave property of logarithm function? No, we can’t because we need a lower bound

Iterative Scaling • Weights still couple with each other • Still need further decomposition

Iterative Scaling

Iterative Scaling Wait a minute, this can not be right! What happens?

Logarithm Bound Algorithm • Start with initial guess • Come up with a lower bounded • Search the optimal solution that maximizes

Iterative Scaling Where does it go wrong?

Iterative Scaling Not zero when = ’

Iterative Scaling Definition of conditional exponential model

Iterative Scaling

Iterative Scaling

Iterative Scaling o How about ? Is this solution unique?

Iterative Scaling o How about negative features?

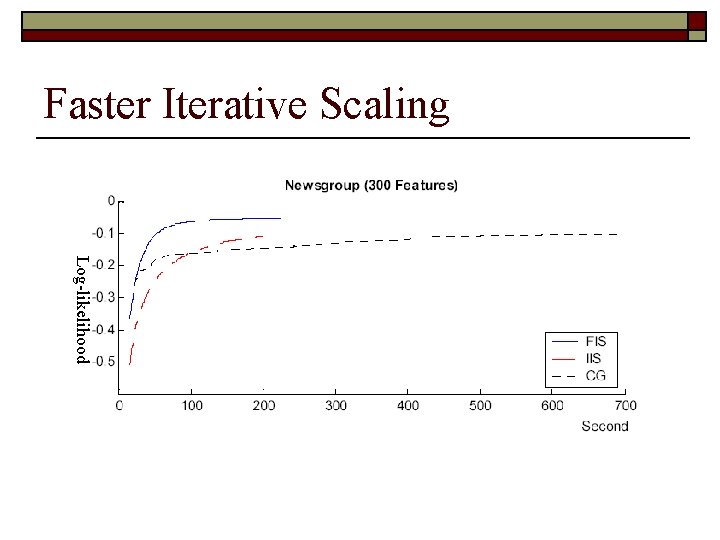
Faster Iterative Scaling o The lower bound may not be tight given all the coupling between weights is removed Univariate functions! o A tighter bound can be derived by not fully decoupling the correlation between weights

Faster Iterative Scaling Log-likelihood

Bad News o o o You may feel great after the struggle of the derivation. However, is iterative scaling a true great idea? Given there have been so many studies in optimization, we should try out existing methods.

Comparing Improved Iterative Scaling to Newton’s Method Dataset Instances Features Rule 29, 602 246 Lex 42, 509 135, 182 Summary Shallow Dataset Iterations Time (s) Rule 823 42. 48 81 1. 13 Try out the standard numerical Lex 241 24, 044 198, 467 methods before you get excited 176 8, 625, 782 about 264, 142 your algorithm Summary 626 Limited-memory Quasi-Newton method Improved iterative scaling Shallow 102. 18 20. 02 208. 22 69 8. 52 3216 71053. 12 421 2420. 30