Expanding two brackets With practice we can expand

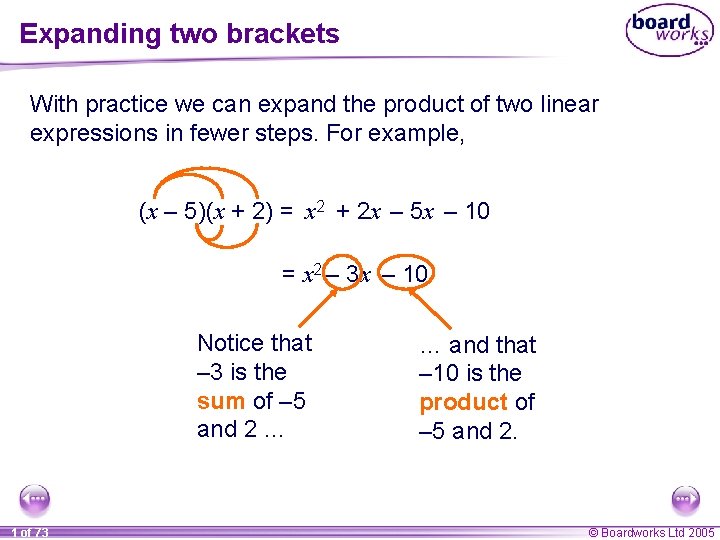
Expanding two brackets With practice we can expand the product of two linear expressions in fewer steps. For example, (x – 5)(x + 2) = x 2 + 2 x – 5 x – 10 = x 2 – 3 x – 10 Notice that – 3 is the sum of – 5 and 2 … 1 of 73 … and that – 10 is the product of – 5 and 2. © Boardworks Ltd 2005

Matching quadratic expressions 1 2 of 73 © Boardworks Ltd 2005

Matching quadratic expressions 2 3 of 73 © Boardworks Ltd 2005

Squaring expressions Expand simplify: (2 – 3 a)2 We can write this as, (2 – 3 a)2 = (2 – 3 a) Expanding, (2 – 3 a) = 2(2 – 3 a) – 3 a(2 – 3 a) = 4 – 6 a + 9 a 2 = 4 – 12 a + 9 a 2 4 of 73 © Boardworks Ltd 2005

Squaring expressions In general, (a + b)2 = a 2 + 2 ab + b 2 The first term squared … … plus 2 × the product of the two terms … … plus the second term squared. For example, (3 m + 2 n)2 = 9 m 2 + 12 mn + 4 n 2 5 of 73 © Boardworks Ltd 2005

Squaring expressions 6 of 73 © Boardworks Ltd 2005

The difference between two squares Expand simplify (2 a + 7)(2 a – 7) Expanding, (2 a + 7)(2 a – 7) = 2 a(2 a – 7) + 7(2 a – 7) = 4 a 2 – 14 a + 14 a – 49 = 4 a 2 – 49 When we simplify, the two middle terms cancel out. This is the difference In general, between two squares. (a + b)(a – b) = a 2 – b 2 7 of 73 © Boardworks Ltd 2005

The difference between two squares 8 of 73 © Boardworks Ltd 2005

Matching the difference between two squares 9 of 73 © Boardworks Ltd 2005

Contents A 1 Algebraic manipulation A A 1. 1 Using index laws A A 1. 2 Multiplying out brackets A A 1. 3 Factorization A A 1. 4 Factorizing quadratic expressions A A 1. 5 Algebraic fractions 10 of 73 © Boardworks Ltd 2005

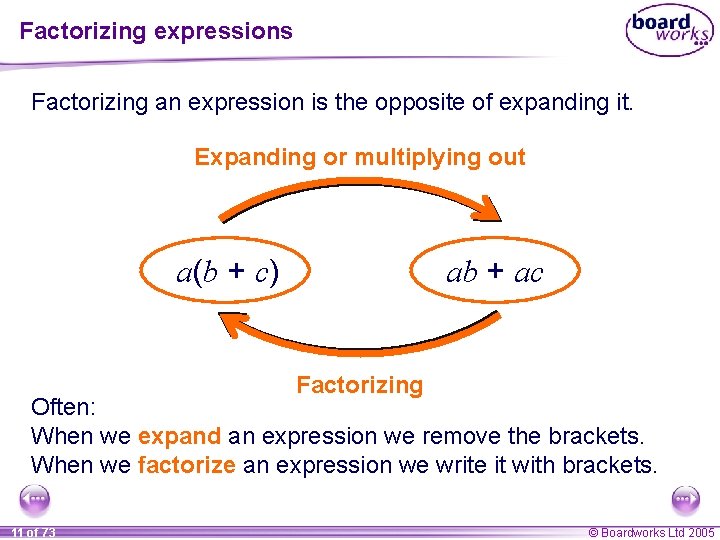
Factorizing expressions Factorizing an expression is the opposite of expanding it. Expanding or multiplying out a(b + c) ab + ac Factorizing Often: When we expand an expression we remove the brackets. When we factorize an expression we write it with brackets. 11 of 73 © Boardworks Ltd 2005

Factorizing expressions Expressions can be factorized by dividing each term by a common factor and writing this outside a pair of brackets. For example, in the expression 5 x + 10 the terms 5 x and 10 have a common factor, 5. We can write the 5 outside of a set of brackets and mentally divide 5 x + 10 by 5. (5 x + 10) ÷ 5 = x + 2 This is written inside the bracket. 5(x + 2) 12 of 73 © Boardworks Ltd 2005

Factorizing expressions Writing 5 x + 10 as 5(x + 2) is called factorizing the expression. Factorize 6 a + 8 13 of 73 Factorize 12 n – 9 n 2 The highest common factor of 6 a and 8 is 2. The highest common factor of 12 n and 9 n 2 is 3 n. (6 a + 8) ÷ 2 = 3 a + 4 (12 n – 9 n 2) ÷ 3 n = 4 – 3 n 6 a + 8 = 2(3 a + 4) 12 n – 9 n 2 = 3 n(4 – 3 n) © Boardworks Ltd 2005

Factorizing expressions Writing 5 x + 10 as 5(x + 2) is called factorizing the expression. Factorize 3 x + x 2 The highest common factor of 3 x and x 2 is x. (3 x + x 2) ÷x=3+x Factorize 2 p + 6 p 2 – 4 p 3 The highest common factor of 2 p, 6 p 2 and 4 p 3 is 2 p. (2 p + 6 p 2 – 4 p 3) ÷ 2 p = 1 + 3 p – 2 p 2 3 x + x 2 = x(3 + x) 2 p + 6 p 2 – 4 p 3 = 2 p(1 + 3 p – 2 p 2) 14 of 73 © Boardworks Ltd 2005

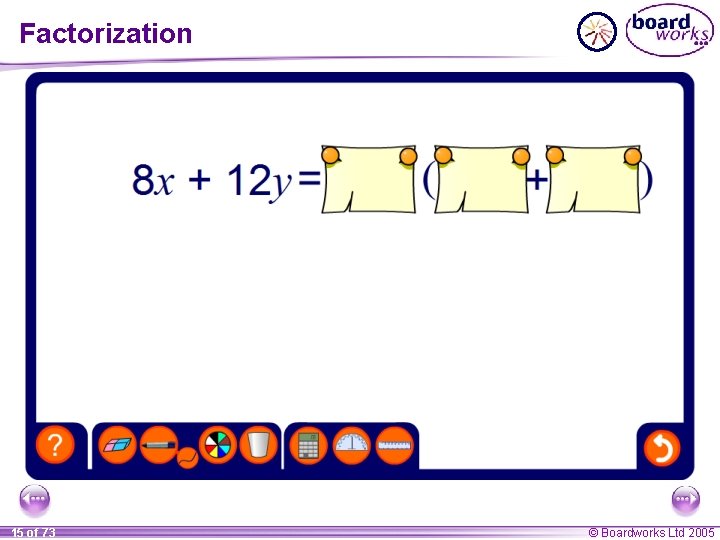
Factorization 15 of 73 © Boardworks Ltd 2005

Factorization by pairing Some expressions containing four terms can be factorized by regrouping the terms into pairs that share a common factor. For example, Factorize 4 a + ab + 4 + b Two terms share a common factor of 4 and the remaining two terms share a common factor of b. 4 a + ab + 4 + b = 4 a + 4 + ab + b = 4(a + 1) + b(a + 1) 4(a + 1) and + b(a + 1) share a common factor of (a + 1) so we can write this as (a + 1)(4 + b) 16 of 73 © Boardworks Ltd 2005

Factorization by pairing Factorize xy – 6 + 2 y – 3 x We can regroup the terms in this expression into two pairs of terms that share a common factor. When we take xy – 6 + 2 y – 3 x = xy + 2 y – 3 x – 6 out a factor of – 3, – 6 = y(x + 2) – 3(x + 2) becomes + 2 y(x + 2) and – 3(x + 2) share a common factor of (x + 2) so we can write this as (x + 2)(y – 3) 17 of 73 © Boardworks Ltd 2005

Contents A 1 Algebraic manipulation A A 1. 1 Using index laws A A 1. 2 Multiplying out brackets A A 1. 3 Factorization A A 1. 4 Factorizing quadratic expressions A A 1. 5 Algebraic fractions 18 of 73 © Boardworks Ltd 2005

Quadratic expressions A quadratic expression is an expression in which the highest power of the variable is 2. For example, 2 t x 2 – 2, w 2 + 3 w + 1, 4 – 5 g 2 , 2 The general form of a quadratic expression in x is: ax 2 + bx + c (where a = 0) x is a variable. a is a fixed number and is the coefficient of x 2. b is a fixed number and is the coefficient of x. c is a fixed number and is a constant term. 19 of 73 © Boardworks Ltd 2005

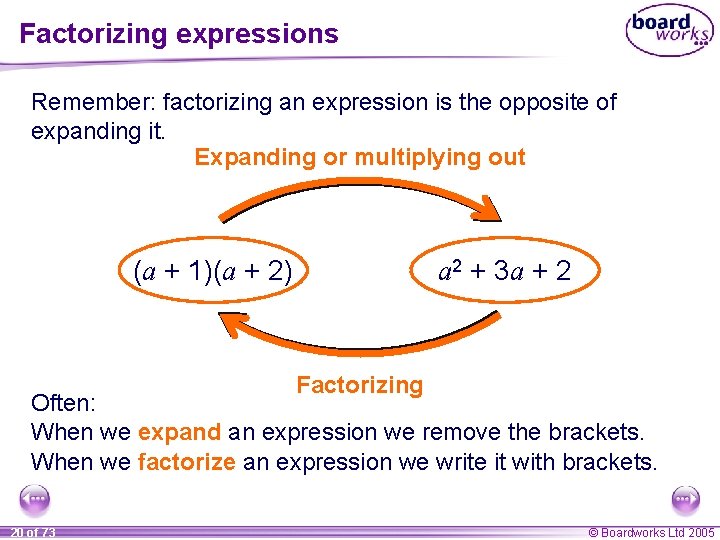
Factorizing expressions Remember: factorizing an expression is the opposite of expanding it. Expanding or multiplying out a 2 + 3 a + 2 (a + 1)(a + 2) Factorizing Often: When we expand an expression we remove the brackets. When we factorize an expression we write it with brackets. 20 of 73 © Boardworks Ltd 2005

Factorizing quadratic expressions Quadratic expressions of the form x 2 + bx + c can be factorized if they can be written using brackets as (x + d)(x + e) where d and e are integers. If we expand (x + d)(x + e) we have, (x + d)(x + e) = x 2 + dx + ex + de = x 2 + (d + e)x + de Comparing this to x 2 + bx + c we can see that: The sum of d and e must be equal to b, the coefficient of x. The product of d and e must be equal to c, the constant term. 21 of 73 © Boardworks Ltd 2005

Factorizing quadratic expressions 1 22 of 73 © Boardworks Ltd 2005

Matching quadratic expressions 1 23 of 73 © Boardworks Ltd 2005

Factorizing quadratic expressions Quadratic expressions of the form ax 2 + bx + c can be factorized if they can be written using brackets as (dx + e)(fx + g) where d, e, f and g are integers. If we expand (dx + e)(fx + g)we have, (dx + e)(fx + g)= dfx 2 + dgx + efx + eg = dfx 2 + (dg + ef)x + eg Comparing this to ax 2 + bx + c we can see that we must choose d, e, f and g such that: a = df, b = (dg + ef) c = eg 24 of 73 © Boardworks Ltd 2005

Factorizing quadratic expressions 2 25 of 73 © Boardworks Ltd 2005

Matching quadratic expressions 2 26 of 73 © Boardworks Ltd 2005

Factorizing the difference between two squares A quadratic expression in the form x 2 – a 2 is called the difference between two squares. The difference between two squares can be factorized as follows: x 2 – a 2 = (x + a)(x – a) For example, 9 x 2 – 16 = (3 x + 4)(3 x – 4) 25 a 2 – 1 = (5 a + 1)(5 a – 1) m 4 – 49 n 2 = (m 2 + 7 n)(m 2 – 7 n) 27 of 73 © Boardworks Ltd 2005

Factorizing the difference between two squares 28 of 73 © Boardworks Ltd 2005

Matching the difference between two squares 29 of 73 © Boardworks Ltd 2005

Contents A 1 Algebraic manipulation A A 1. 1 Using index laws A A 1. 2 Multiplying out brackets A A 1. 3 Factorization A A 1. 4 Factorizing quadratic expressions A A 1. 5 Algebraic fractions 30 of 73 © Boardworks Ltd 2005

Algebraic fractions 3 x 2 a and are examples of algebraic fractions. 2 4 x 3 a + 2 The rules that apply to numerical fractions also apply to algebraic fractions. For example, if we multiply or divide the numerator or the denominator of a fraction by the same number or term we produce an equivalent fraction. For example, 3 y 3(a + 2) 3 x 3 6 = = 2 4 x 4 x 8 x 4 xy 4 x(a + 2) 31 of 73 © Boardworks Ltd 2005

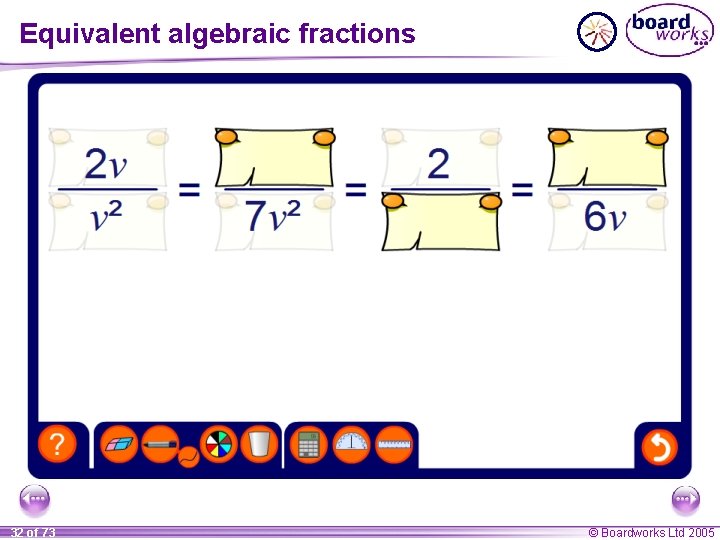
Equivalent algebraic fractions 32 of 73 © Boardworks Ltd 2005

Simplifying algebraic fractions We simplify or cancel algebraic fractions in the same way as numerical fractions, by dividing the numerator and the denominator by common factors. For example, 6 ab Simplify 3 ab 2 2 6 ab 6×a×b = 2 3 ab 3×a×b×b 2 = b 33 of 73 © Boardworks Ltd 2005

Simplifying algebraic fractions Sometimes we need to factorize the numerator and the denominator before we can simplify an algebraic fraction. For example, 2 a + a 2 Simplify 8 + 4 a 2 a + a 2 8 + 4 a a (2 + a) = 4(2 + a) a = 4 34 of 73 © Boardworks Ltd 2005

Simplifying algebraic fractions b 2 – 36 is the difference between two squares. b 2 – 36 Simplify 3 b – 18 (b + 6)(b – 6) b 2 – 36 = 3(b – 6) 3 b – 18 b+6 3 If required, we can write this as = b b 6 + = + 2 3 35 of 73 © Boardworks Ltd 2005

Manipulating algebraic fractions Remember, a fraction written in the form a+b c can be written as a b + c c However, a fraction written in the form c a+b cannot be written as c c + a b For example, 1+2 3 36 of 73 1 2 = + 3 3 but 3 1+2 3 3 = + 1 2 © Boardworks Ltd 2005

Multiplying and dividing algebraic fractions We can multiply and divide algebraic fractions using the same rules that we use for numerical fractions. In general, and, For example, a c ac × = b d bd a c a d ad ÷ = × = b d b c bc 3 6 p 3 p 3 p 2 = × = 2(1 – p) 4(1 – p) 4 2 37 of 73 © Boardworks Ltd 2005

Multiplying and dividing algebraic fractions 2 4 ? What is ÷ 3 y – 6 y– 2 2 3 y – 6 2 4 ÷ = y– 2 3 y – 6 This is the reciprocal 4 of y– 2 × 4 y– 2 2 = × 3(y – 2) 4 2 1 = 6 38 of 73 © Boardworks Ltd 2005

Adding algebraic fractions We can add algebraic fractions using the same method that we use for numerical fractions. For example, 1 2 What is + ? a b We need to write the fractions over a common denominator before we can add them. b 2 a b + 2 a 1 2 + = a b ab ab ab In general, a c ad + bc + = b d bd 39 of 73 © Boardworks Ltd 2005

Adding algebraic fractions y 3 What is + ? x 2 We need to write the fractions over a common denominator before we can add them. y y×x 3 3× 2 + = + x x× 2 2×x 2 xy 6 + = 2 x 2 x 6 + xy = 2 x 40 of 73 © Boardworks Ltd 2005

Subtracting algebraic fractions We can also subtract algebraic fractions using the same method as we use for numerical fractions. For example, p q What is – ? 3 2 We need to write the fractions over a common denominator before we can subtract them. p q 2 p 3 q 2 p – 3 q – = 3 2 6 6 6 In general, a c ad – bc – = b d bd 41 of 73 © Boardworks Ltd 2005

Subtracting algebraic fractions 2+p 3 What is – ? 2 q 4 2+p 3 (2 + p) × 2 q 3× 4 – = – 2 q 4 4 × 2 q 2 q × 4 2 q(2 + p) 12 = – 8 q 8 q 2 q(2 + p) – 12 = 8 q 4 6 q(2 + p) – 6 = 4 q 42 of 73 © Boardworks Ltd 2005

Addition pyramid – algebraic fractions 43 of 73 © Boardworks Ltd 2005