Expanding Brackets double Expressions with two sets of

Expanding Brackets - double

Expressions with two sets of brackets Example Expand (y + 2)(y + 3) How can we do this? 1. Distributive Law Each term in the first bracket is multiplied by the second bracket = y(y + 3 ) + 2(y + 3) = y 2 + 3 y + 2 y + 6 = y 2 + 5 y + 6 Using distributive process Expanding each single bracket Collecting like terms Note: This is known as a quadratic expression (the highest power of x is 2)

Representing as rectangles 2. Representing as rectangles Once again, this can be represented by the area of a rectangle, which is subdivided into smaller parts, each area represents one of the 4 parts of the expanded distributive expression y + 2 y + 3 y 2 3 y 2 y 6 y(y + 3) + 2(y + 3) =y 2 +3 y +2 y +6 = y 2 + 5 y + 6 The area for each region can be worked out systematically. - be careful of negative signs!!

Expressions with two sets of brackets Another way of looking at it is by making each area proportional to the term in the expression y i. e. + 1+1 y y 2 y y +1 +1 +1 y y y 1 1 1 We can then simply cross multiply then add common terms y 2 + 5 y +6

Summary: To expand the product of two brackets: 1. Each term in the first bracket is multiplied by each term in the second bracket • Be careful with the sign in front of each term 2. Add or subtract any like terms Example:

An example with negatives: A more complex example:

A useful method to remember: The acronym FOIL is a useful way to remember which items are multiplied together: If we write a generalised form for a two bracket equation as F First terms (a + b)(c + d) = ac O Outside terms (a + b)(c + d) = ad I Inside terms (a + b)(c + d) = bc L Last terms (a + b)(c + d) = bd Putting together gives us: (a + b)(c + d) = ac + ad + bc + bd (a + b)(c + d)

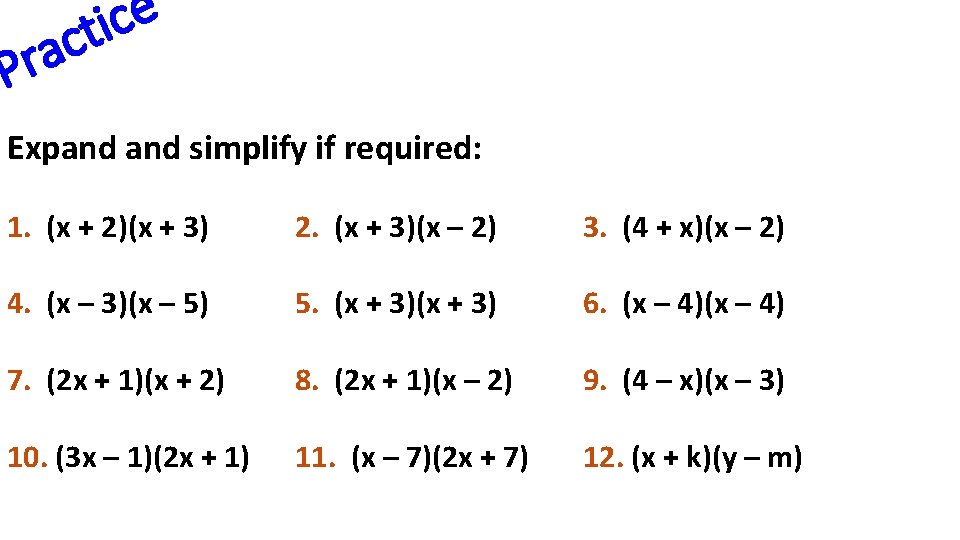
a r P e c i t c Expand simplify if required: 1. (x + 2)(x + 3) 2. (x + 3)(x – 2) 3. (4 + x)(x – 2) 4. (x – 3)(x – 5) 5. (x + 3) 6. (x – 4) 7. (2 x + 1)(x + 2) 8. (2 x + 1)(x – 2) 9. (4 – x)(x – 3) 10. (3 x – 1)(2 x + 1) 11. (x – 7)(2 x + 7) 12. (x + k)(y – m)