EXPANDER GRAPHS Properties Applications Things to cover n

EXPANDER GRAPHS Properties & Applications

Things to cover ! n n Definitions Properties n n Constructions n n Combinatorial, Spectral properties “Explicit” constructions Applications n Networks, Complexity, Coding theory, Sampling, Derandomization

Intuitive Definition n n Intuitively: a graph for which any “small” subset of vertices has a relatively “large” neighborhood. Conceivably: it allows to build networks with guaranteed access for making connections or routing messages. n Removing random edges (local connection failures) does not reduce the property of an expander by much! Fault-tolerance

Graph Theory Vocabulary n n n Neighborhood of a vertex v: Neighborhood of U V: Boundary of U: d-regular graph : every vertex has degree d Definition 1: a d-regular graph is a (d, c)-expander or has a cexpansion (for some positive c) iff for every subset U V of size at most|V|/2,

Remark! n Routing a messages from a node A to another node B in an (d, c) expander graph: n n n At least (1+d)(1+c) nodes at distance 2 from A Further away, (1+d) (1+c)k nodes at distance k from A Continue until having a reachable set of nodes VA that has more than |V|/2 nodes: the node B may not be in VA Starting from B, we eventually obtain a set VB that has more that |V|/2. The sets VA and VB must overlap There is a path of length 2(k+1) from A to B, where k=logc+1|V|/2 larger c implies shorter path

Simple Result n n Proposition: For all c > 0 and for all sufficiently large n, there exists NO (2, c)-expander graph with n vertices. Proof: without loss of generality, assume that the graph is connected. Consider a connected subset of n/2 vertices. Its boundary is of size 2. Choose the number of vertices in the graph such that c. n/2 > 2!

Isoperimetric Constants n n Expanding constant = Isoperimetric constant: The boundary is expressed either in terms of vertices or in terms of edges.

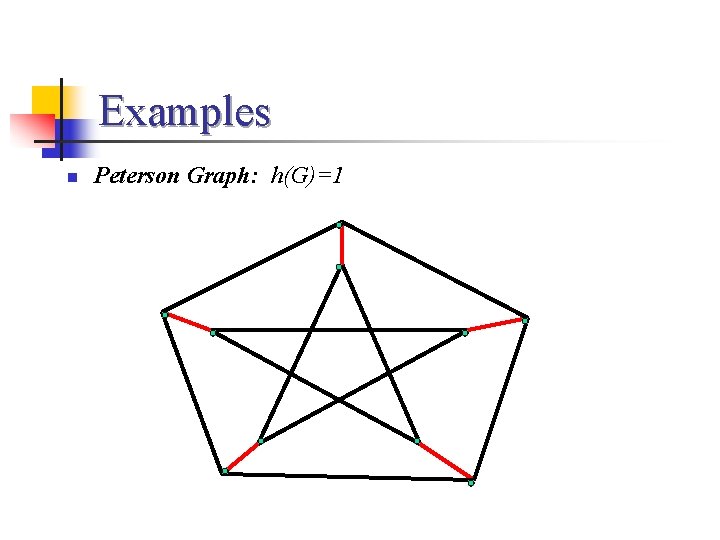
Examples n Peterson Graph: h(G)=1

Examples n n Complete Graph Kn of n vertices: If |U|=l then the boundary of U has l(n-l) edges so that h(Kn)=n-[n/2]~n/2 Cycle Cn of n vertices: if |U|=n/2 then the boudary of U has 2 edges, so that h(Cn) 4/n

Definition n Definition 2: a family (Gn) of finite connected k-regular graphs is a family of expanders if |Vn| when n and there exists > 0 such that h(Gn) for every n. Comments: k-regularity assumption included to assure that the number of edges of Gn grows linearly with the number of vertices. Hence a family of complete graphs is a bad example. Optimization problem: best connectivity from a minimal number of edges.

Spectral Properties n n Adjacency matrix A: Aij=number of edges joining vi to vj. It is n-by-n symmetric matrix and it has n real eigenvalues counting multiplicities: 0 … n-1 Proposition 1. 1: let G be a k-regular graph of n vertices, then: (1) The largest eigenvalue 0 = k (2) All eigenvalues i for 1 i n-1 satisfy | i| k (3) 0 has multiplicity 1 iff G is connected

Spectral Properties n n Bipartite Graphs: it is possible to paint the vertices with two colors in such a way no two adjacent vertices have the same color. Proposition 1. 2: let G be a connected, k-regular graph of n vertices. The following are equivalent: (1) G is bipartite (2) The spectrum of G is symmetric about 0 (3) The smallest eigenvalue is n-1 = -k n Spectral Gap of G: k - 1= 0 - 1

Spectral Properties n n n Theorem 1. 1: Let G be a finite connected k-regular graph without loops. Then: Rephrasing the main problem: Give a construction for a family of finite connected k-regular graphs (Gn) such that |Vn| when n and there exists > 0 for which k 1(Gn) for every n. Observation 1. 1: To have good quality expanders, the spectral gap need to be as large as possible.

Spectral Properties n n Theorem 1. 2: Let (Gn) be a family of finite connected k-regular graph with |Vn| when n . Then: Observation 1. 2: the spectral gap cannot be arbitrary large! Definition: a finite connected k-regular graph G is Ramanujan if for every eigenvalue k, A family of Ramanujan graphs is an optimal solution from the spectral perspective.

Some Expanders! n Theorem 1. 3: For the following values of k, there exists infinite families of k-regular Ramanujan graphs: n k = p + 1, p an odd prime (Lubotzky-Philips-Sarnak, Margulis) n n n Algebraic groups, modular forms, Riemann Hypothesis for curves over finite fields. k = 3 (Chiu) k = q + 1, q is prime power (Morgenstern)

Constructibiliy n n n Consider a family of expander graphs (GN) and assume that N = 2 n for some n, and that the vertices of GN are the 2 n strings of length n. Weak Constructibility: GN is weakly constructible if an explicit representation of it can be given in polynomial time of N. Strong Constructibility: GN is strongly constructible if when given an n-bit long vertex of GN we can construct a list of all its neighbors in polynomial time of n.

Some Explicit Constructions n Gabber and Galil: the first construction with an explicitly given constant vertex expansion. n n Bipartite Graph: V = A B where |A| = |B| = m 2 and vertices in A and B are indexed by ordered pairs in [m]x[m]. Then, where the addition is done modulo m. The degree of this graph is 5 and the vertex expansion for a set of size s is where n is the number of vertices. Reingold, Vadhan, and Wigderson: simple combinatorial construction of constant-degree expander graphs using the zig-zag graph product!

Amplification of Expanders n n Need: some applications need an expansion coefficient that is larger than the one associated with a constructed (GN). Amplify (GN) (GNk) How: add (u, v) such that there exists a path of length exactly k between u and v in GNk. Spectral consequence: MNk = (MN)k Proposition: if GN is a d-regular graph with expansion coefficient c, then GNk satisfies: (1) It is dk-regular (2) Its expansion coefficient is (1 + c)k - 1 (3) If GN is weakly constructible, so does GNk

An Application of Expanders n n n Problem: Let W be a set of witnesses {0, 1}n of size at least 2 n-1. Give a randomized algorithm A such that when given < ½ satisfies: Pr[A outputs an a witness of W] > 1 - Trivial solution: pick –log( ) strings independently, each giving a probability of at least ½ to hit W. Restrictions: running time should be poly(n/ ), and at most n bits of randomness are allowed to be used.

An Application of Expanders n Using Expanders: start with a d-regular expander graph GN with expansion c, the construct Gl. N by choosing l = log(1/ )/log(1 + c) new expansion coefficient ~ 1/. n n n Select at random a vertex in Gl. N Scan the neighbors of v, and output a neighbor in W if such exists, else fail Remarks: each vertex is represented as a string of n bits, thus only n bits of randomness are required. Complexity: poly(n. dl) = poly(n/ ) Correctness: fails with probability at most .

More Applications n n n Random walk on expanders: taking an l step random walk in an expander graph is in a way similar to choosing l vertices at random: Uniform independent sampling with less random bits! Cryptography: again using random walks on constructive expanders, one can transform any regular weak one-way function (easily inverted on all but a polynomial fraction of the range) into a strong one while preserving security. Complexity: amplification of success probability of randomized algorithms.

More Applications n Coding theory: asymptotically good error correcting codes based on expanders.