Exercises on AVLTree CSC 2100 c Data Structure

Exercises on AVL-Tree CSC 2100 c Data Structure Tutorial 11 Andrew Mo mzmo@cse. cuhk. edu. hk

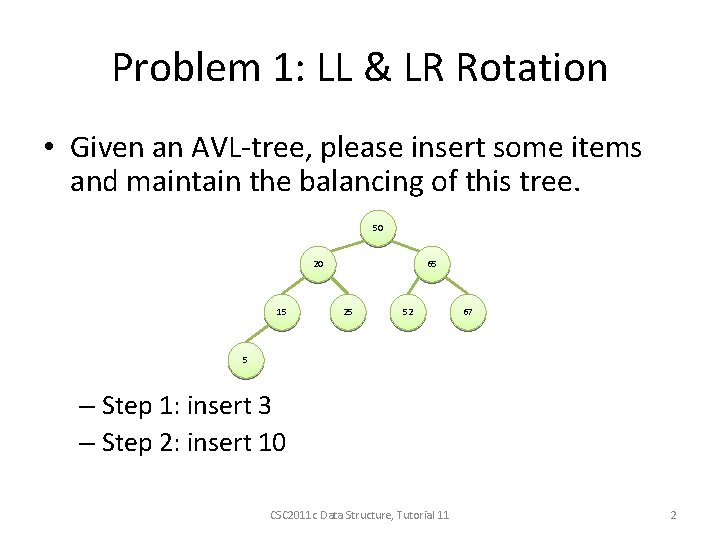
Problem 1: LL & LR Rotation • Given an AVL-tree, please insert some items and maintain the balancing of this tree. 50 20 15 65 25 52 67 5 – Step 1: insert 3 – Step 2: insert 10 CSC 2011 c Data Structure, Tutorial 11 2

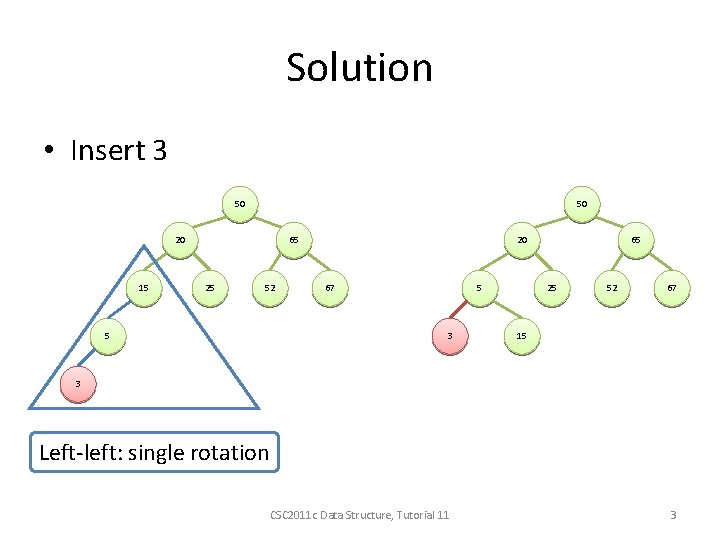
Solution • Insert 3 50 50 20 15 65 25 52 5 20 67 5 3 65 25 52 67 15 3 Left-left: single rotation CSC 2011 c Data Structure, Tutorial 11 3

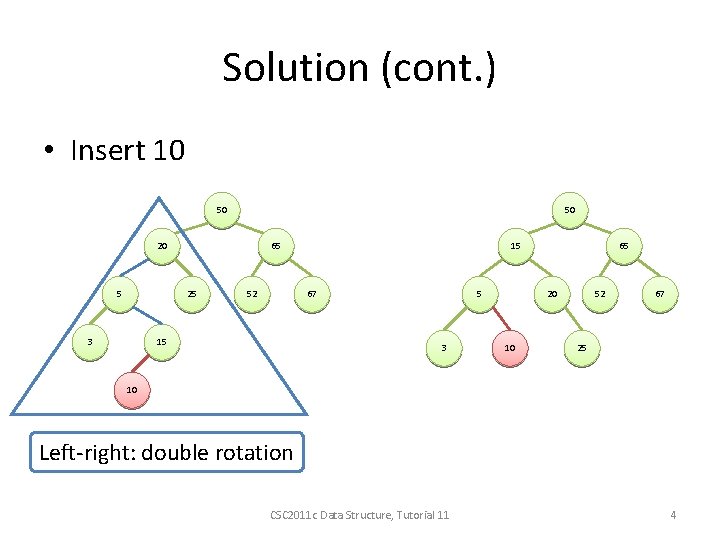
Solution (cont. ) • Insert 10 50 50 20 5 65 25 3 52 15 67 15 5 3 65 20 10 52 67 25 10 Left-right: double rotation CSC 2011 c Data Structure, Tutorial 11 4

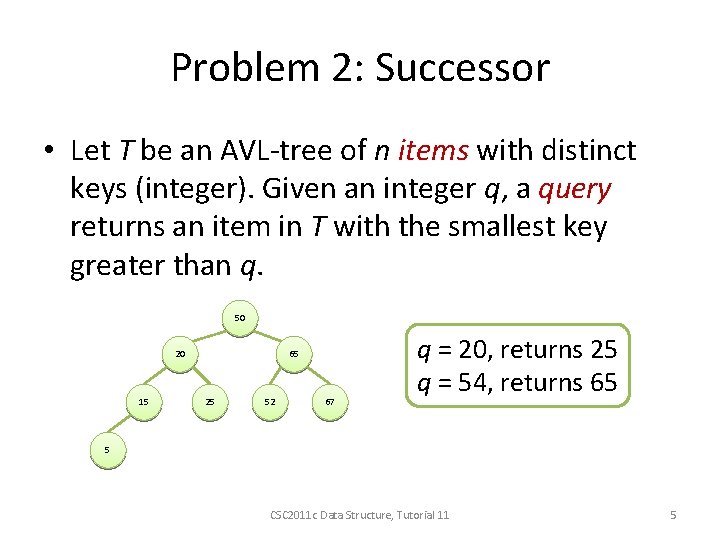
Problem 2: Successor • Let T be an AVL-tree of n items with distinct keys (integer). Given an integer q, a query returns an item in T with the smallest key greater than q. 50 20 15 65 25 52 67 q = 20, returns 25 q = 54, returns 65 5 CSC 2011 c Data Structure, Tutorial 11 5

Solution 1. Search T from the root item, and maintain a possible result r initialized with infinite. 2. The key of the current searching item is x. – If x <= q, scan the root of the right sub-tree of the current searching item – If x > q (possibly, x is the result) 1) Update r, r = x 2) Scan the root of the left sub-tree of the current searching item 3. If the current searching item is not empty, repeat step 2. 4. Output r (infinite means no satisfied answer). CSC 2011 c Data Structure, Tutorial 11 6

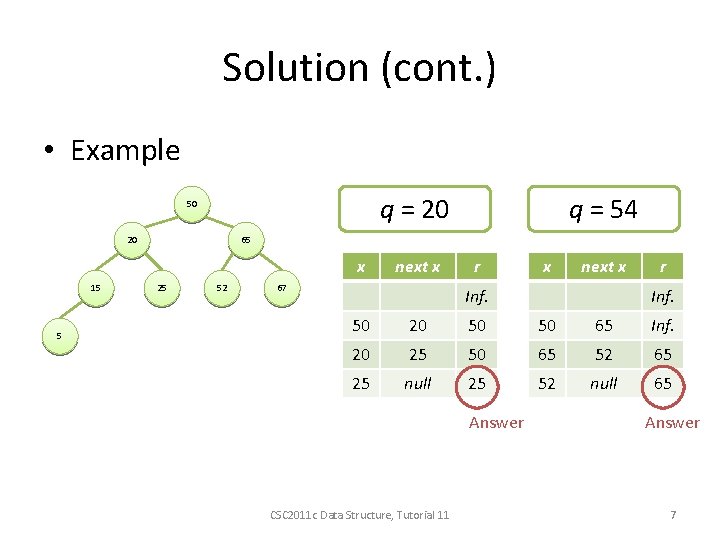
Solution (cont. ) • Example q = 20 50 20 65 x 15 5 q = 54 25 52 next x 67 r x next x Inf. r Inf. 50 20 50 50 65 Inf. 20 25 50 65 52 65 25 null 25 52 null 65 Answer CSC 2011 c Data Structure, Tutorial 11 Answer 7

Problem 3: Range Report • Let S be a set of integers. Given an interval I = (a, b), a query returns all integers belonging to S∩I. • There are many queries all the time. Between any two queries, there may be some integer insertion operations of S (S is dynamic). • Please design a data structure that consumes O(log n) time in processing an insertion operation of S and answers a query in O(log n + k) time, where n is the current size of S and k is the number of reported integers. CSC 2011 c Data Structure, Tutorial 11 8

Problem 3: Range Report (cont. ) • Example S = {5, 15, 20, 25, 50, 52, 65, 67} Query: I = (23, 60) Insert: 10, 45 Query: I = (5, 60) Output 25, 50, 52 15, 10, 25, 45, 50, 52 CSC 2011 c Data Structure, Tutorial 11 9

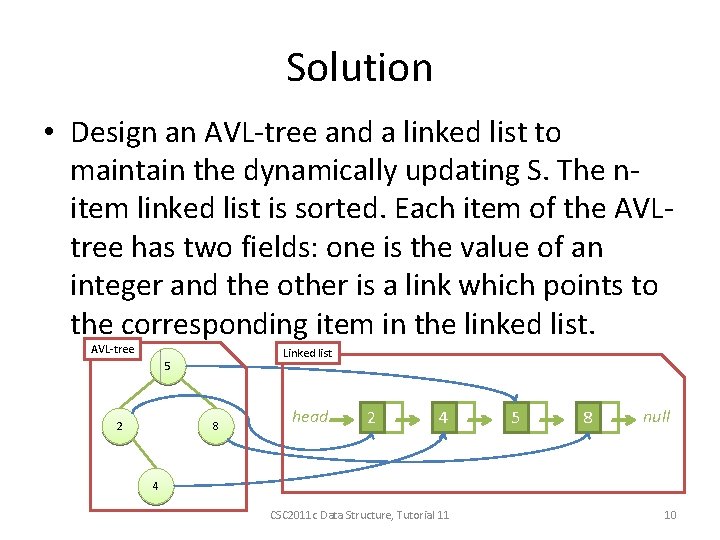
Solution • Design an AVL-tree and a linked list to maintain the dynamically updating S. The nitem linked list is sorted. Each item of the AVLtree has two fields: one is the value of an integer and the other is a link which points to the corresponding item in the linked list. AVL-tree Linked list 5 2 8 head 2 4 5 8 null 4 CSC 2011 c Data Structure, Tutorial 11 10

Solution (cont. ) • Inserting operation 1. Insert the integer x into the AVL-tree. 2. Utilize Predecessor() to find the maximum integer k less than x in the AVL-tree. 3. Insert an item in the linked list after k. • Complexity – O(log n) + O(1) – Overall: O(log n) CSC 2011 c Data Structure, Tutorial 11 11

Solution (cont. ) • Answering a query 1. For I = (a, b), utilize Successor() to find the minimum integer m larger than a in the AVL-tree. 2. Locate the position of m in the linked list. 3. Search the linked list from m until the condition that the value of the item is larger than or equal to b. • Complexity – O(log n) + O(1) + O(k) – Overall: O(log n + k) CSC 2011 c Data Structure, Tutorial 11 12