Exercise Name the property of addition illustrated a






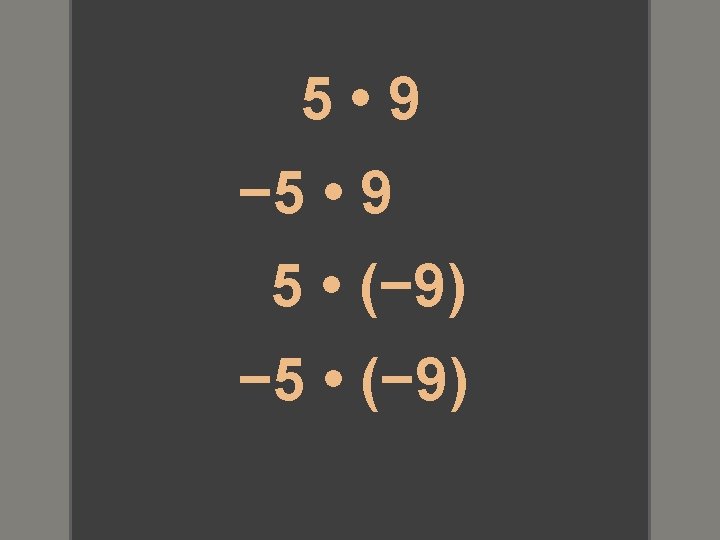

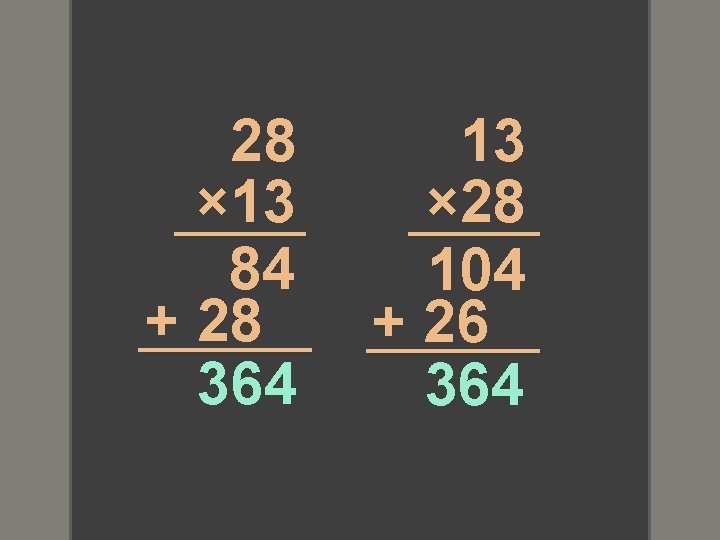



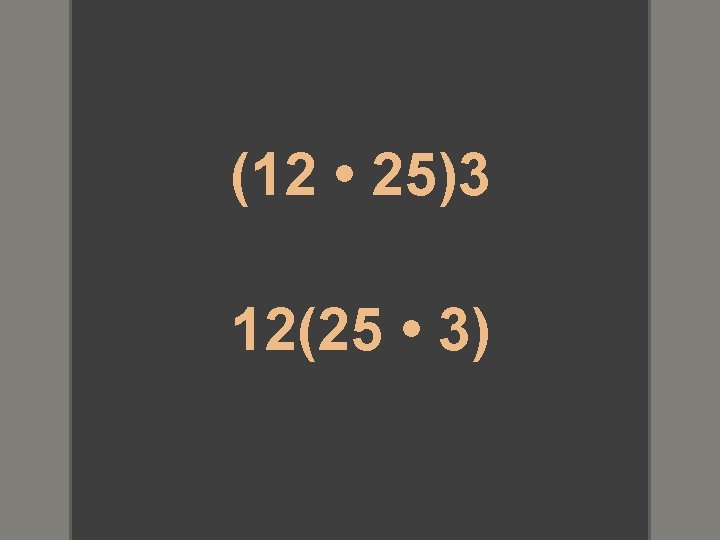












![Example Simplify: − 4 x[3 x(− 5 x)] 60 x 3 Example Simplify: − 4 x[3 x(− 5 x)] 60 x 3](https://slidetodoc.com/presentation_image_h2/97fd49749e40fc90a348993fc1e36f53/image-26.jpg)



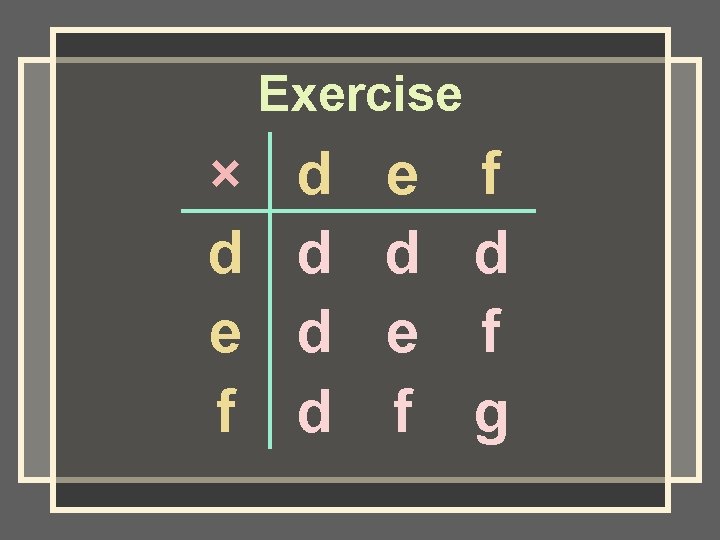


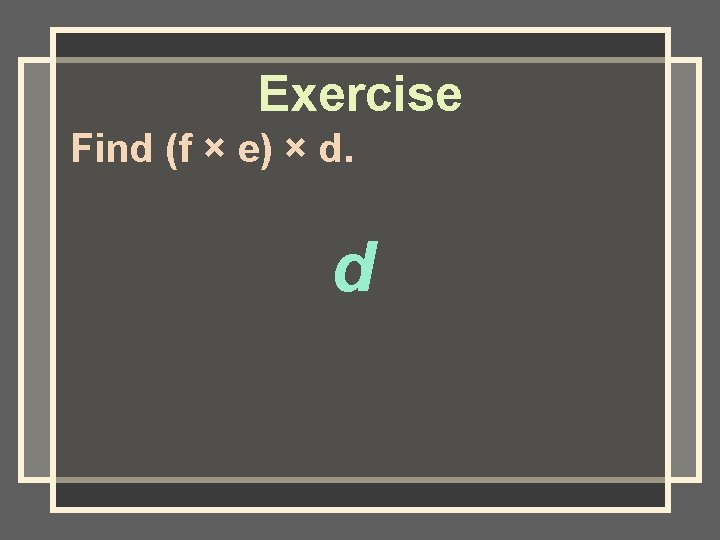
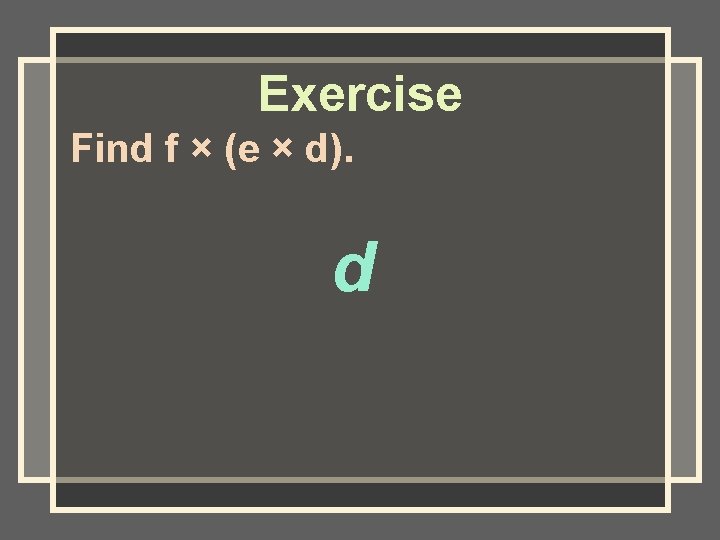
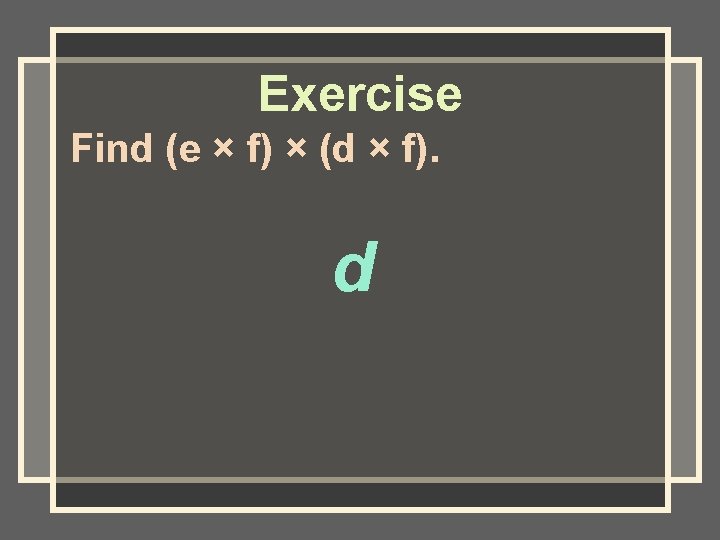



- Slides: 39

Exercise Name the property of addition illustrated. (a + b) + c = (b + a) + c Commutative

Exercise Name the property of addition illustrated. (a + b) + c = a + (b + c) Associative

Exercise Name the property of addition illustrated. (a + b) + 0 = (a + b) Identity

Exercise Name the property of addition illustrated. a + (–a) = 0 Inverse

Exercise Name the property of addition illustrated. The sum of any two negative integers is a negative integer. Closure

Closure Property of Multiplication For all integers a and b, ab is an integer.
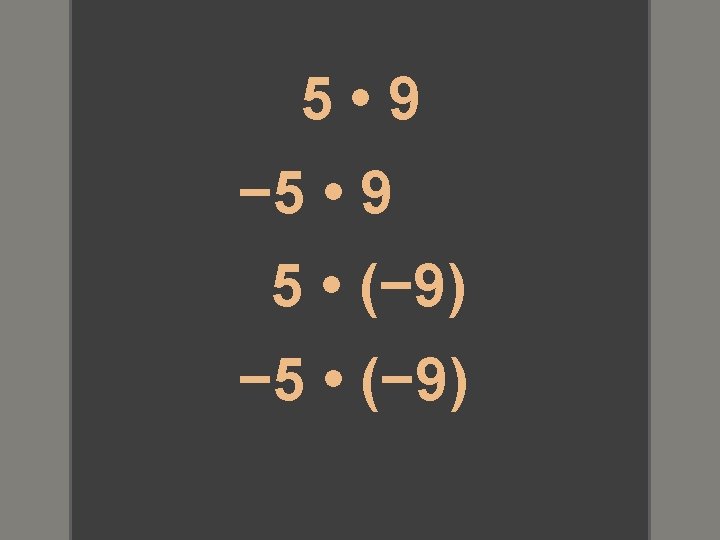

Commutative Property of Multiplication For all integers a and b, ab = ba.
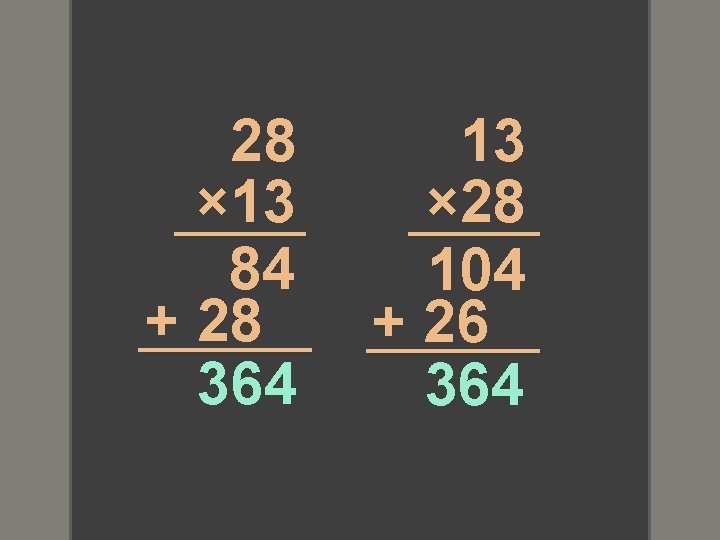
28 × 13 84 + 28 364 13 × 28 104 + 26 364

3(2) or 2(3) BUT 7 x not x 7

Example 1 Use the Commutative Property to write an equivalent expression for each of the following. a. 6(− 9) − 9(6) b. xy yx

Associative Property of Multiplication For any integers a, b, and c, (ab)c = a(bc).
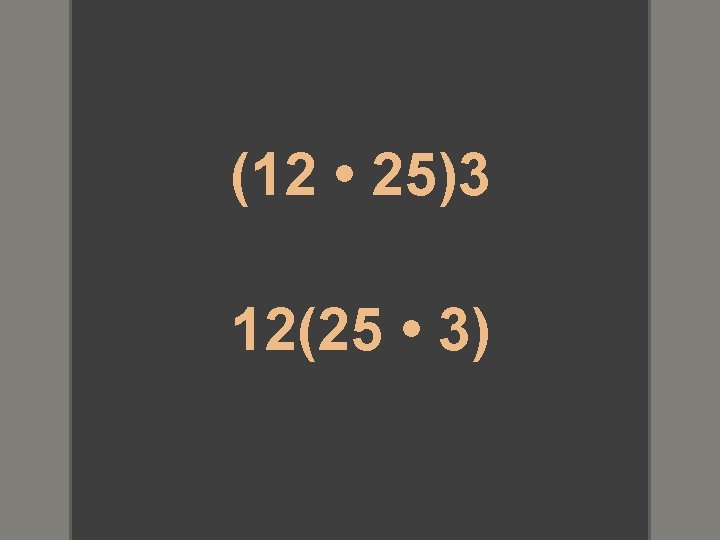
(12 • 25)3 12(25 • 3)

Example 2 Use the Associative Property to write an equivalent expression for each of the following. a. (− 7 • 8)4 − 7(8 • 4) b. 3(5 n) (3 • 5)n

Identity Property of Multiplication For any integer a, a × 1 = 1 × a = a.

Example 3 Use the Identity Property to write an equivalent expression for each of the following. a. 1(− 42) b. 1 x − 42 x

Zero Property of Multiplication For any integer a, a × 0 = 0 × a = 0.

Property of Multiplication Closure: for all integers a and b, ab is an integer. Commutative: ab = ba Associative: (ab)c = a(bc) Description Example The product of any two integers is an integer. − 7 × 2 = − 14; − 14 is an integer. Changing the order of the factors does not change the product. Changing the grouping of the factors does not change the product. − 6(− 5) = − 5(− 6) [− 5(4)]9 = − 5[4(9)]

Property of Description Multiplication Identity: a × 1 The product of any =1×a=a integer and one equals the original integer. Zero: a × 0 = The product of any 0×a=0 integer and zero equals zero. Example − 7(1) = 1(− 7) = − 7 0(5, 210) = 5, 210(0) = 0

Example Name the property of multiplication illustrated. 6(− 8) = (− 8)6 Commutative

Example Name the property of multiplication illustrated. 12(0) = 0 Zero

Example Name the property of multiplication illustrated. Since − 7 and − 9 are integers, − 7(− 9) is an integer. Closure

Example Name the property of multiplication illustrated. 16(1) = 16 Identity

Example Name the property of multiplication illustrated. 4 n(6 n)3 = 4 n(3)6 n Commutative

Example Name the property of multiplication illustrated. 4(6 n) = 24 n Associative
![Example Simplify 4 x3 x 5 x 60 x 3 Example Simplify: − 4 x[3 x(− 5 x)] 60 x 3](https://slidetodoc.com/presentation_image_h2/97fd49749e40fc90a348993fc1e36f53/image-26.jpg)
Example Simplify: − 4 x[3 x(− 5 x)] 60 x 3

Example Simplify: n(− 4)n − 4 n 2

Example Simplify: 60(− 4)x − 4 x

Example Simplify: 3(20 − 70) 0
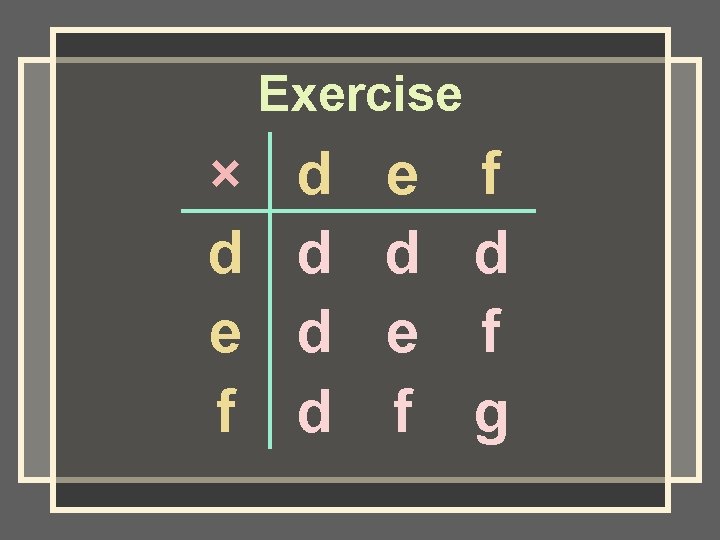
Exercise × d e f d f g

Exercise Is the set closed for multiplication? Why? No; f × f = g, but g is not in the set.

Exercise Is the set commutative? Why? Yes, the products are the same when the order changes. For example: d • e = d and e • d = d.
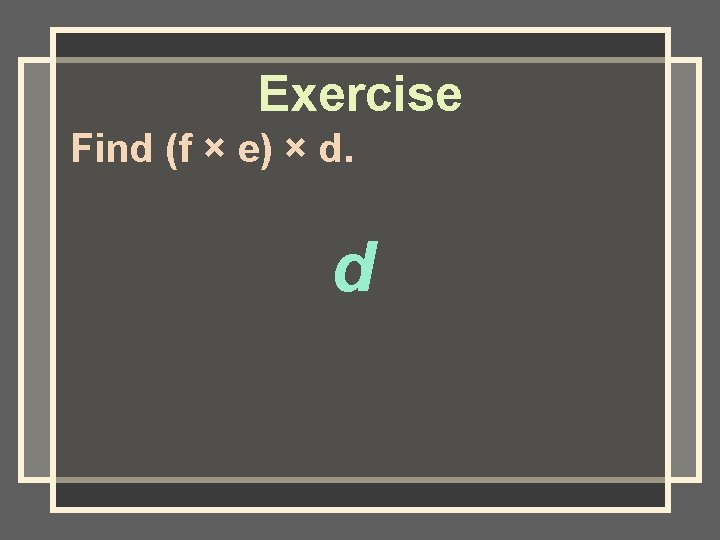
Exercise Find (f × e) × d. d
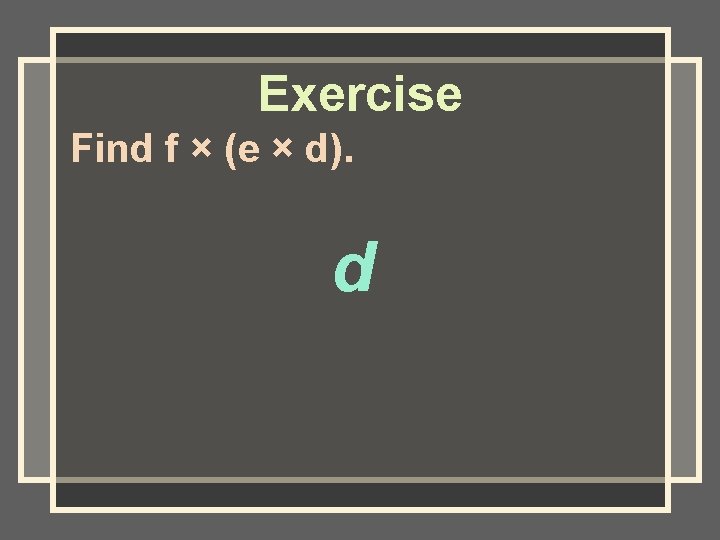
Exercise Find f × (e × d). d
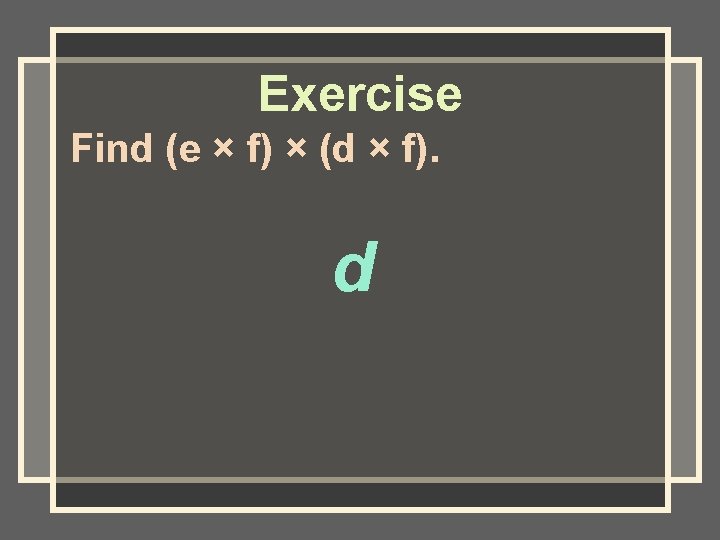
Exercise Find (e × f) × (d × f). d

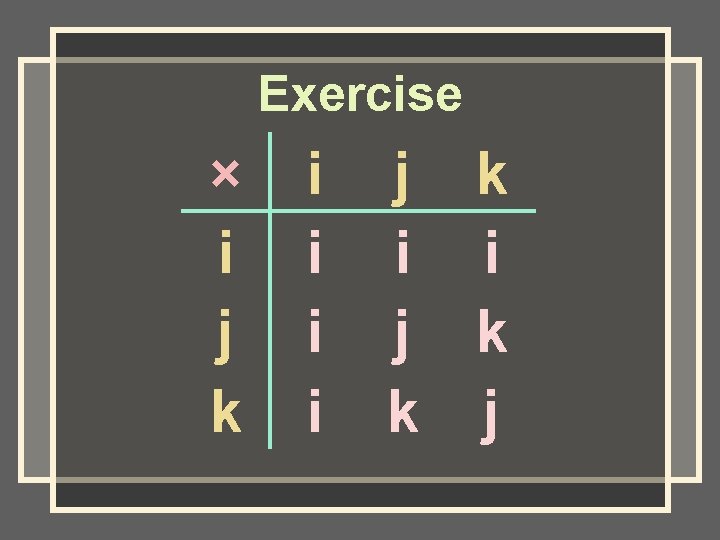
Exercise × i j k i i j k k j

Exercise Is the set closed for multiplication? Why? Yes; all products are in the set.

Exercise Is the set commutative? Why? Yes; changing the order does not change the product.

Exercise Which element is the identity element? Why? j; any element times j equals that element.