Exercise Give the domain and range of the
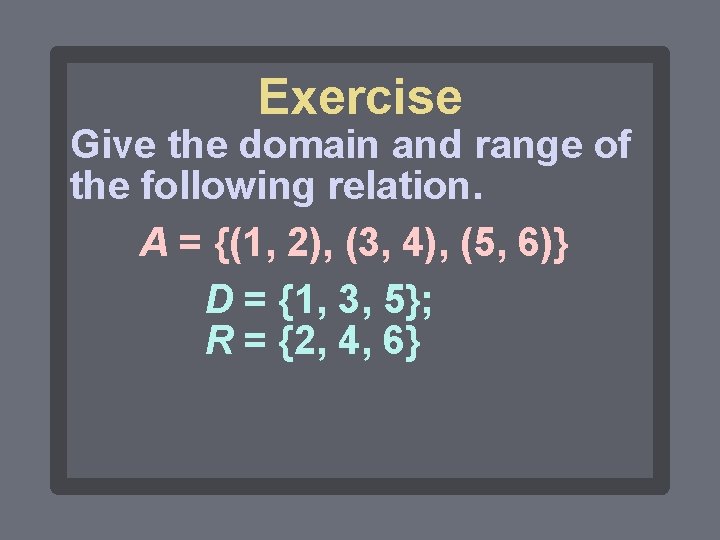
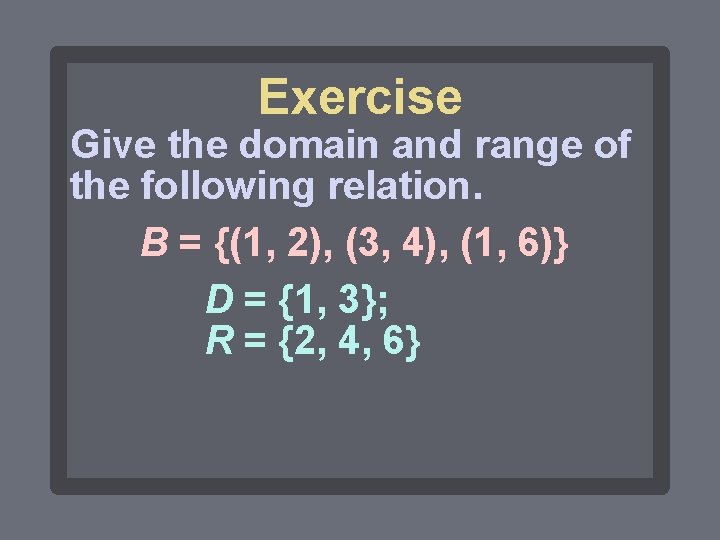
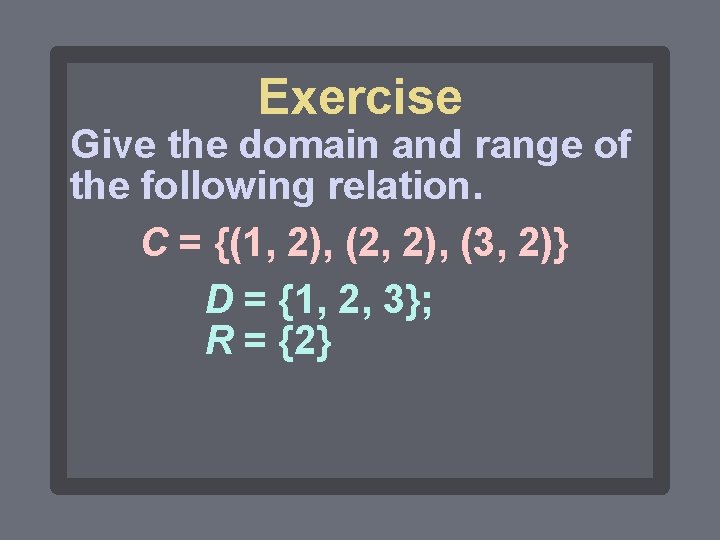
























- Slides: 35
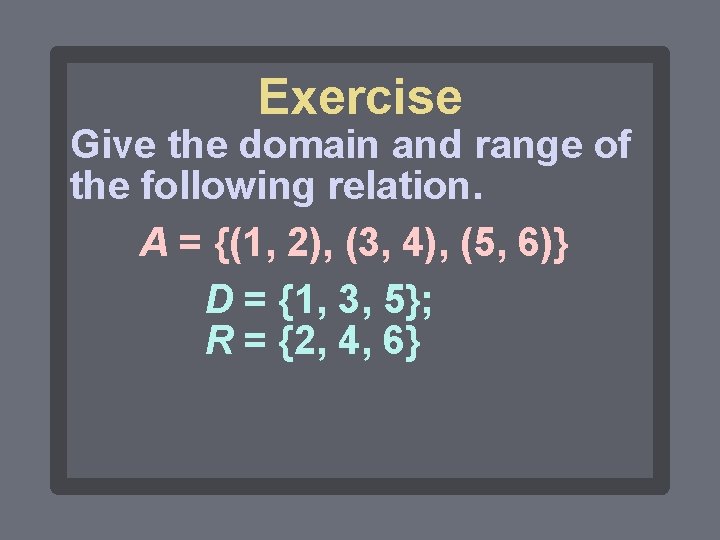
Exercise Give the domain and range of the following relation. A = {(1, 2), (3, 4), (5, 6)} D = {1, 3, 5}; R = {2, 4, 6}
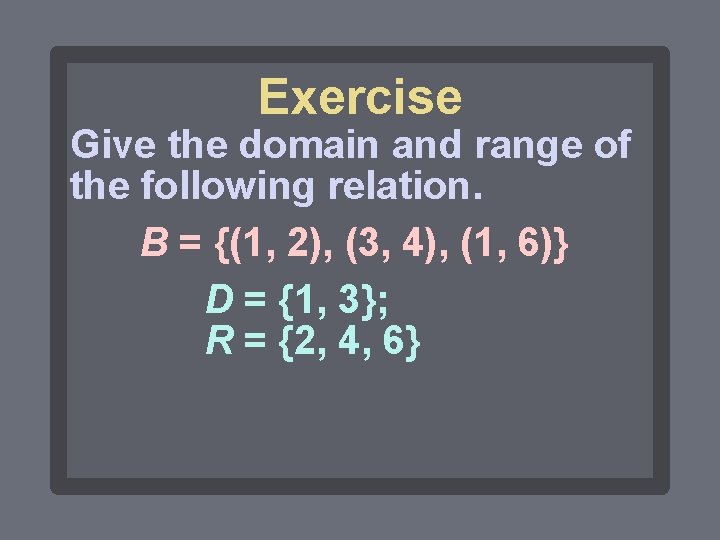
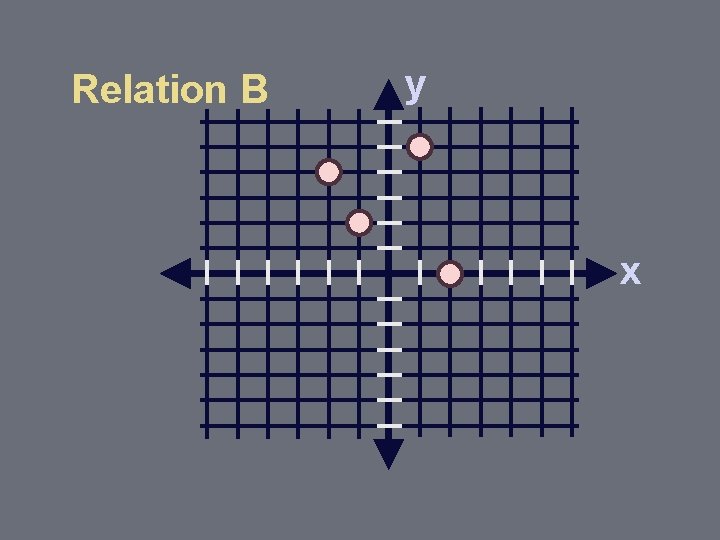
Exercise Give the domain and range of the following relation. B = {(1, 2), (3, 4), (1, 6)} D = {1, 3}; R = {2, 4, 6}
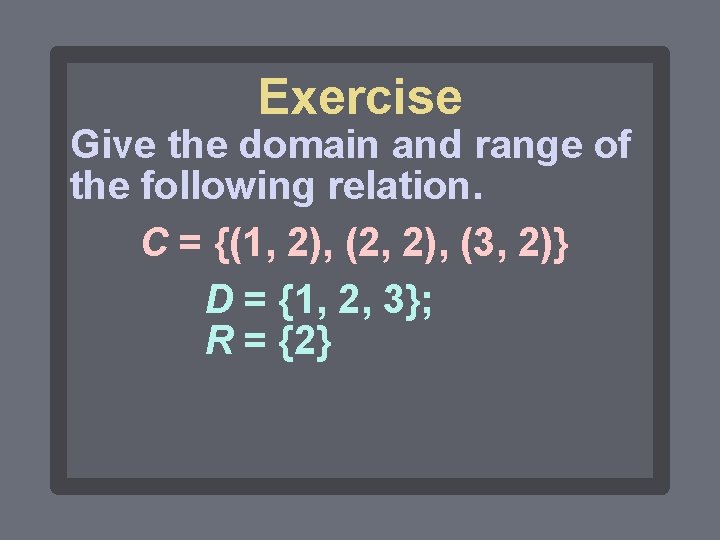
Exercise Give the domain and range of the following relation. C = {(1, 2), (2, 2), (3, 2)} D = {1, 2, 3}; R = {2}

Exercise Give the domain and range of the following relation. D = {(2, 1), (2, 2), (2, 3)} D = {2}; R = {1, 2, 3}

Exercise Is the following set a relation? E = {1, 2, 3, 4} no

Exercise Is the following set a relation? F = {1, 2, 3} no

Function A function is a relation in which no two ordered pairs have the same first coordinate.

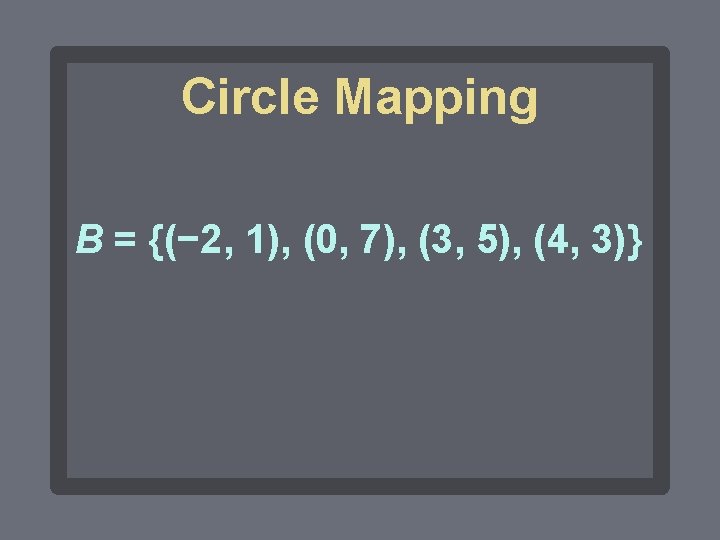
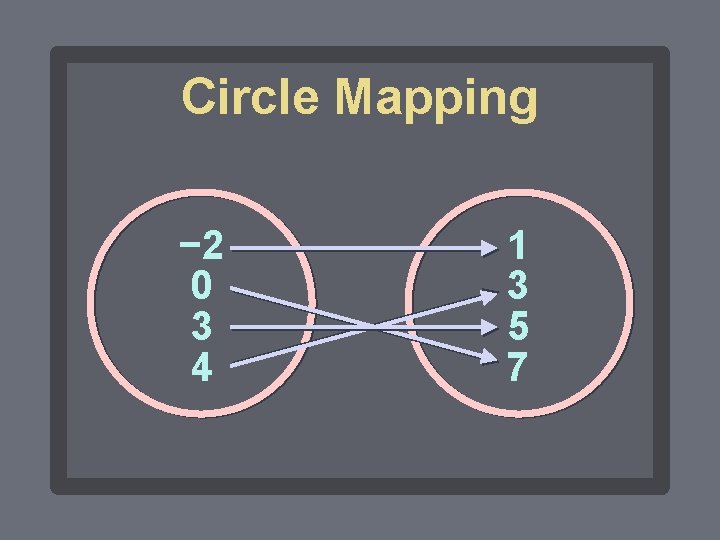
Circle Mapping B = {(− 2, 1), (0, 7), (3, 5), (4, 3)}

Circle Mapping − 2 0 3 4 1 3 5 7

A relation is a function if the circle mapping has only one arrow coming from each element in the domain.

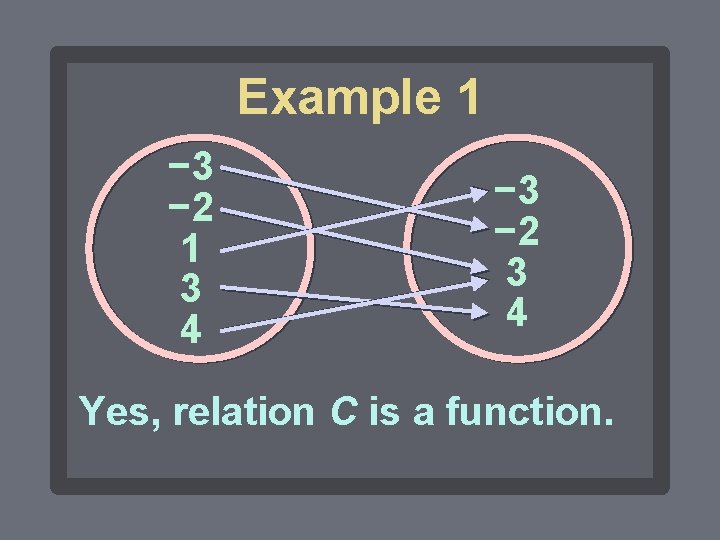
Example 1 Make a circle mapping of relation C, and give the domain and range. Is the relation a function? C = {(− 3, − 2), (− 2, 3), (1, − 3), (3, 4), (4, 3)} D = {− 3, − 2, 1, 3, 4}; R = {− 3, − 2, 3, 4}

Example 1 − 3 − 2 1 3 4 − 3 − 2 3 4 Yes, relation C is a function.

Example 2 Determine whether the relation is a function. Explain your answer. M = {(1, 5), (3, 4), (2, 3), (3, 3)} No. Two ordered pairs have the same x-coordinate.

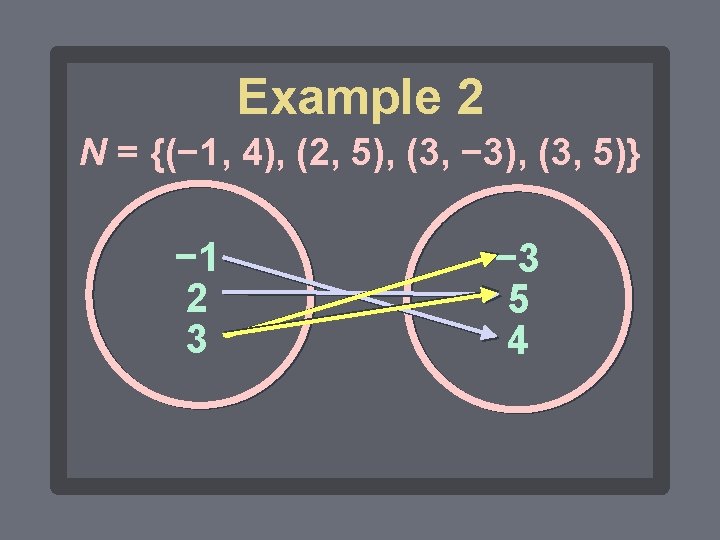
Example 2 Determine whether the relation is a function. Explain your answer. N = {(− 1, 4), (2, 5), (3, − 3), (3, 5)} No. Two ordered pairs have the same x-coordinate.


Example 3 Is P = {(− 3, 6), (1, 6), (2, 6)} a function? Yes. No two points have the same first coordinate.

The letters f and g often denote functions.

f = {(− 3, 4), (0, 3), (3, − 2)} Domain of f = {− 3, 0, 3} Range of f = {− 2, 3, 4}

Each element of the range is called a value of the function.

f = {(− 3, 4), (0, 3), (3, − 2)} Because the ordered pair (0, 3) is a part of the function, we say that the value of function f at 0 is 3.

Standard function notation: f (0) = 3 f of zero equals three.

For ordered pairs (x, y) the value of f at x is y, written f(x) = y.

Example 4 Find the following values for function g = {(− 1, 1), (0, 2), (1, 3)}. g(1) = 3, since 1 is paired with 3.

Example 4 Find the following values for function g = {(− 1, 1), (0, 2), (1, 3)}. g(0) = 2, since 0 is paired with 2.

Example 4 Find the following values for function g = {(− 1, 1), (0, 2), (1, 3)}. g(− 1) = 1, since − 1 is paired with 1.

Example 5 Find the following values for function f(x) = 2 x + 4. f(3) = 2(3) + 4 f=6+4 f = 10

Example 5 Find the following values for function f(x) = 2 x + 4. f(− 3) = 2(− 3) + 4 f = − 6 + 4 f = − 2

Example 6 Find the range of function g(x) = 3 x − 2 for the domain {− 3, 0, 2}. Then write the function as a set of ordered pairs. Find g(x) for each value of the domain.


Example 6 The range of g(x) is {− 11, − 2, 4}. The function is g = {(− 3, − 11), (0, − 2), (2, 4)}.

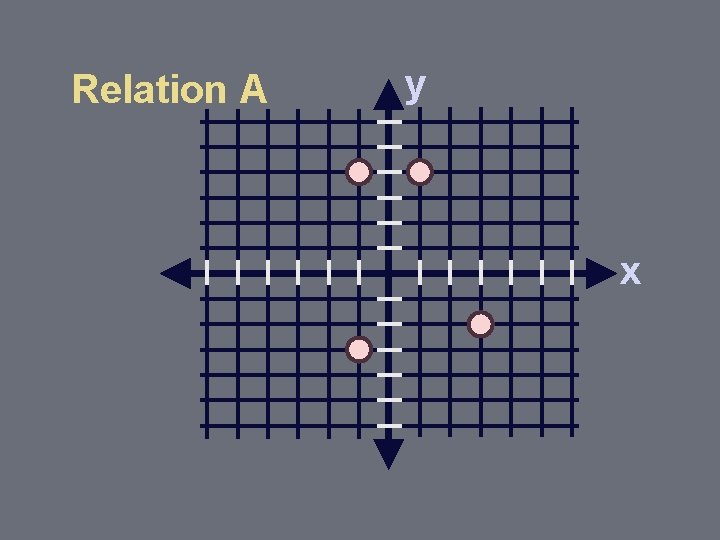
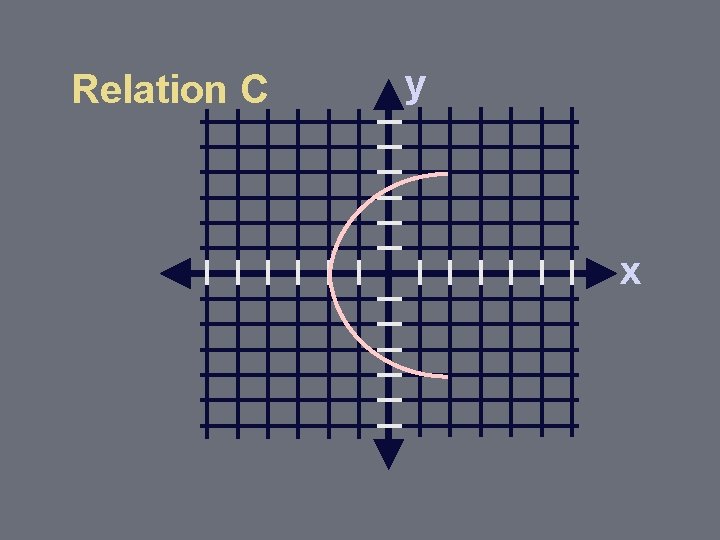
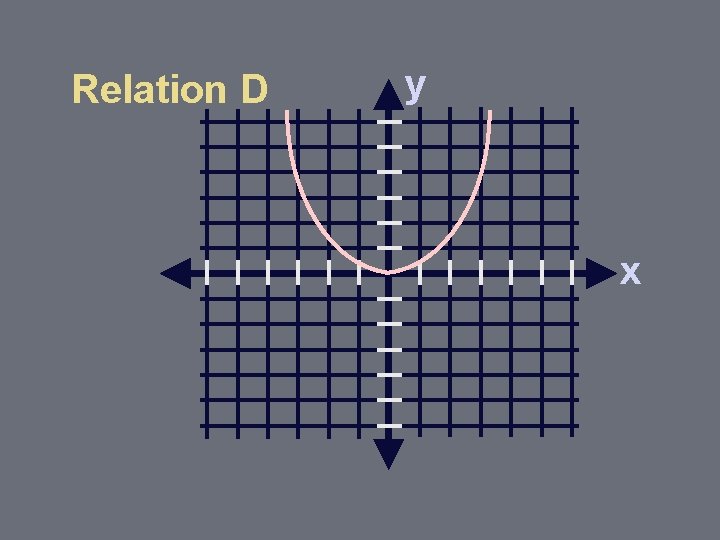
Vertical Line Test for Functions If 2 or more points of the relation lie on the same vertical line, the relation is NOT a function.

Relation A y x

Relation B y x

Relation C y x

Relation D y x