Exercise 143 Draw SFD and BMD for the

Exercise 143 Draw SFD and BMD for the single side overhanging beam subjected to loading as shown below. Determine the absolute maximum bending moment and shear forces and mark them on SFD and BMD. Also locate points of contra flexure if any. A C 4 m 5 k. N 2 k. N 10 k. N/m D B 1 m 2 m

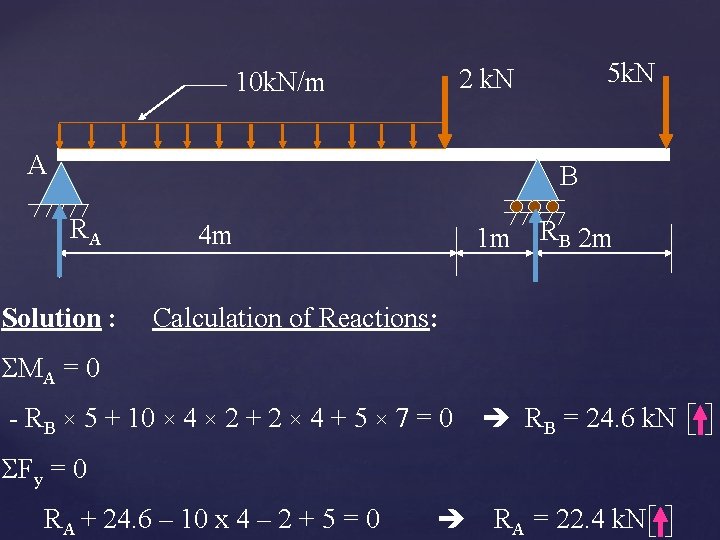
5 k. N 2 k. N 10 k. N/m A B RA Solution : 1 m RB 2 m 4 m Calculation of Reactions: ΣMA = 0 - RB × 5 + 10 × 4 × 2 + 2 × 4 + 5 × 7 = 0 RB = 24. 6 k. N ΣFy = 0 RA + 24. 6 – 10 x 4 – 2 + 5 = 0 RA = 22. 4 k. N

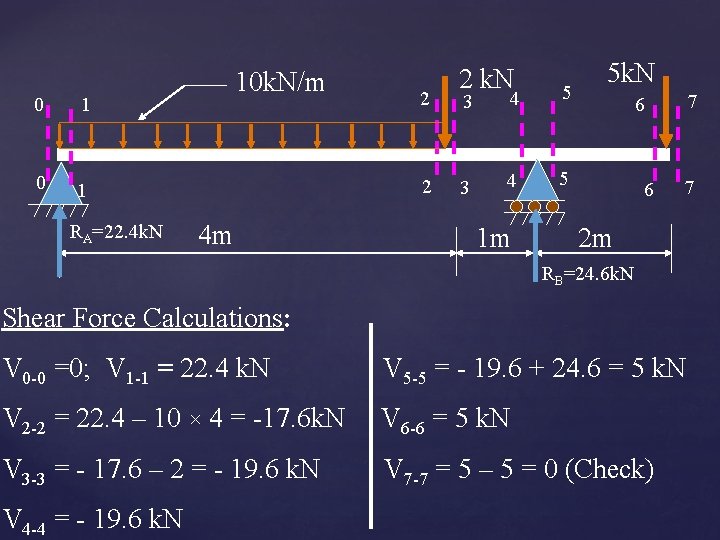
0 1 RA=22. 4 k. N 10 k. N/m 2 2 4 m 2 k. N 3 4 5 1 m 5 k. N 7 6 6 7 2 m RB=24. 6 k. N Shear Force Calculations: V 0 -0 =0; V 1 -1 = 22. 4 k. N V 5 -5 = - 19. 6 + 24. 6 = 5 k. N V 2 -2 = 22. 4 – 10 × 4 = -17. 6 k. N V 6 -6 = 5 k. N V 3 -3 = - 17. 6 – 2 = - 19. 6 k. N V 7 -7 = 5 – 5 = 0 (Check) V 4 -4 = - 19. 6 k. N

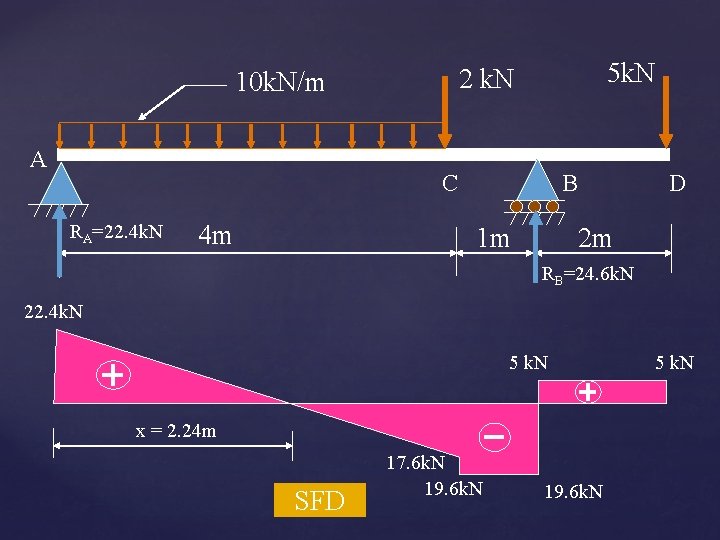
A 5 k. N 2 k. N 10 k. N/m C RA=22. 4 k. N 4 m B 1 m D 2 m RB=24. 6 k. N 22. 4 k. N 5 k. N x = 2. 24 m SFD 17. 6 k. N 19. 6 k. N 5 k. N

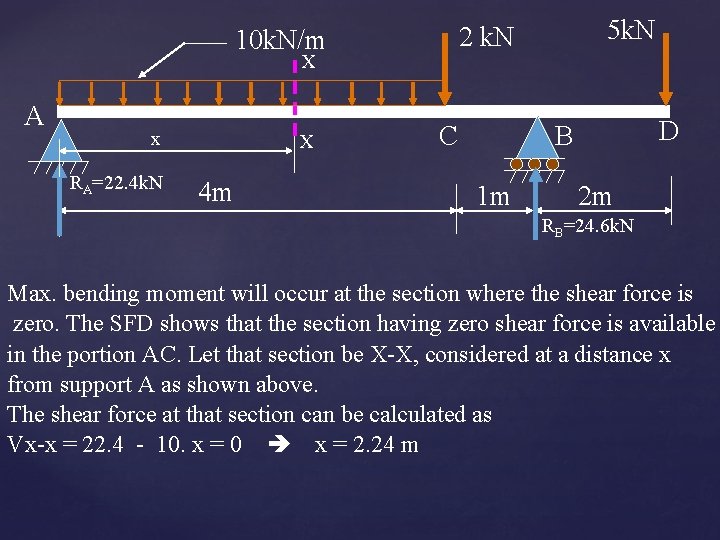
X A x RA=22. 4 k. N X 4 m 5 k. N 2 k. N 10 k. N/m C D B 1 m 2 m RB=24. 6 k. N Max. bending moment will occur at the section where the shear force is zero. The SFD shows that the section having zero shear force is available in the portion AC. Let that section be X-X, considered at a distance x from support A as shown above. The shear force at that section can be calculated as Vx-x = 22. 4 - 10. x = 0 x = 2. 24 m

A C RA=22. 4 k. N 4 m 5 k. N 2 k. N 10 k. N/m D B 1 m 2 m RB=24. 6 k. N Calculations of Bending Moments: MA = M D = 0 MC = 22. 4 × 4 – 10 × 4 × 2 = 9. 6 k. Nm MB = 22. 4 × 5 – 10 × 4 × 3 – 2 × 1 = - 10 k. Nm (Considering Left portion of the section) Alternatively MB = -5 × 2 = -10 k. Nm (Considering Right portion of the section) Absolute Maximum Bending Moment is at X- X , Mmax = 22. 4 × 2. 24 – 10 × (2. 24)2 / 2 = 25. 1 k. Nm

X A x = 2. 24 m RA=22. 4 k. N X C 4 m D B 1 m 2 m RB=24. 6 k. N Mmax = 25. 1 k. Nm 9. 6 k. Nm BMD 5 k. N 2 k. N 10 k. N/m Point of contra flexure 10 k. Nm

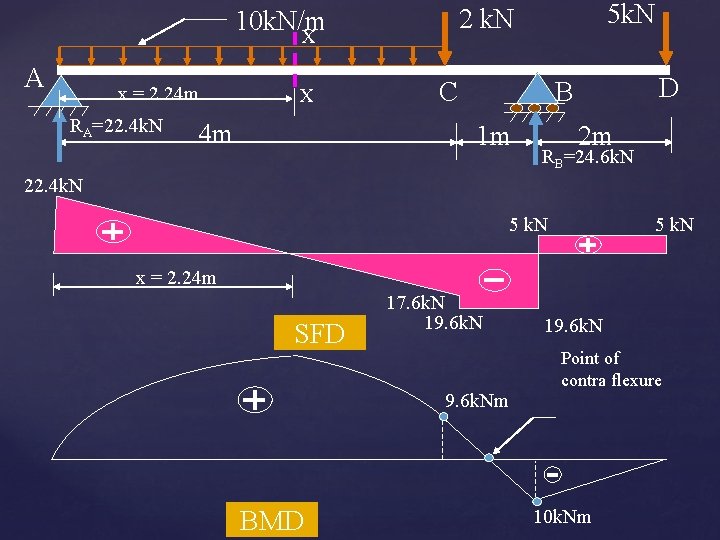
A x = 2. 24 m RA=22. 4 k. N X 4 m 5 k. N 2 k. N 10 k. N/m X C D B 1 m 2 m RB=24. 6 k. N 22. 4 k. N 5 k. N x = 2. 24 m SFD 17. 6 k. N 19. 6 k. Nm BMD 19. 6 k. N Point of contra flexure 10 k. Nm

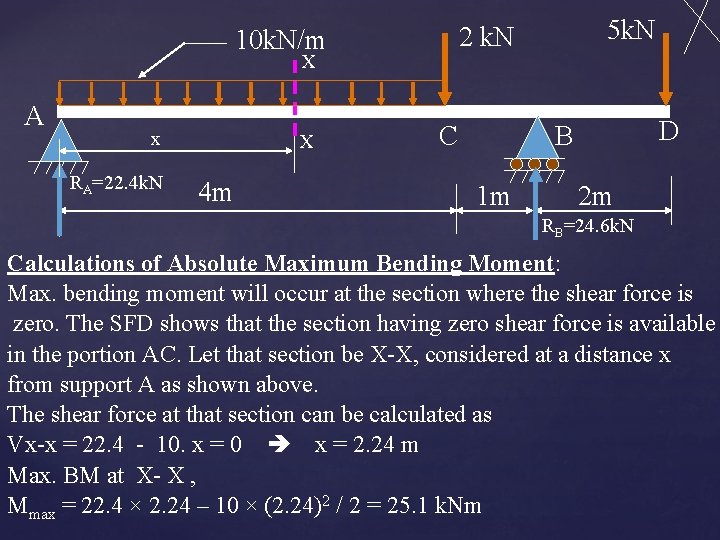
X A x RA=22. 4 k. N X 4 m 5 k. N 2 k. N 10 k. N/m C D B 1 m 2 m RB=24. 6 k. N Calculations of Absolute Maximum Bending Moment: Max. bending moment will occur at the section where the shear force is zero. The SFD shows that the section having zero shear force is available in the portion AC. Let that section be X-X, considered at a distance x from support A as shown above. The shear force at that section can be calculated as Vx-x = 22. 4 - 10. x = 0 x = 2. 24 m Max. BM at X- X , Mmax = 22. 4 × 2. 24 – 10 × (2. 24)2 / 2 = 25. 1 k. Nm

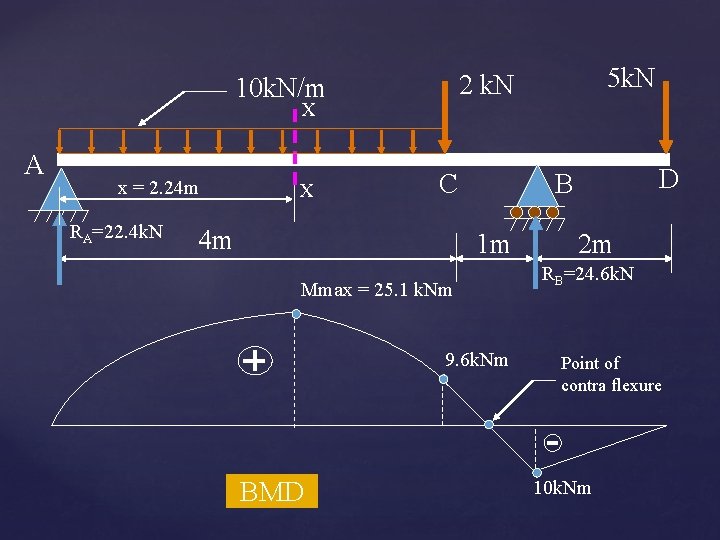
X A x = 2. 24 m RA=22. 4 k. N X C 4 m D B 1 m Mmax = 25. 1 k. Nm 9. 6 k. Nm BMD 5 k. N 2 k. N 10 k. N/m 2 m RB=24. 6 k. N Point of contra flexure 10 k. Nm

Let a be the distance of point of contra flexure from support B Taking moments at the section A-A (Considering left portion) A a = 0. 51 m Mmax = 25. 1 k. Nm 9. 6 k. Nm BMD A a Point of contra flexure 10 k. Nm

30 k. N Parabola 30 k. N x = 1. 5 m 10 k. N SFD 50 k. N Parabola 20 k. Nm 10 k. Nm 50 k. N Point of contra flexure Cubic parabola BMD 20 k. Nm