EXCITEDSTATE QUANTUM PHASE TRANSITIONS IN SYSTEMS WITH FEW

EXCITED-STATE QUANTUM PHASE TRANSITIONS IN SYSTEMS WITH FEW DEGREES OF FREEDOM Pavel Stránský www. pavelstransky. cz Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México In collaboration with: Pavel Cejnar Institute of Particle and Nuclear Phycics, Faculty of Mathematics and Physics, Charles University in Prague, Czech Republic Michal Macek, Amiram Leviatan Racah Institute of Physics, The Hebrew University, Jerusalem, Israel Seminario Lunch Nuclear, Instituto de Física, UNAM 4 th October 2013

1. Excited-state quantum phase transition 2. Models - CUSP potential (1 degree of freedom) - Creagh-Whelan potential (2 degrees of freedom) 3. Signatures of the ESQPT - level density and its derivatives - thermodynamical properties - flow rate

1. Excited-State Quantum Phase Transitions

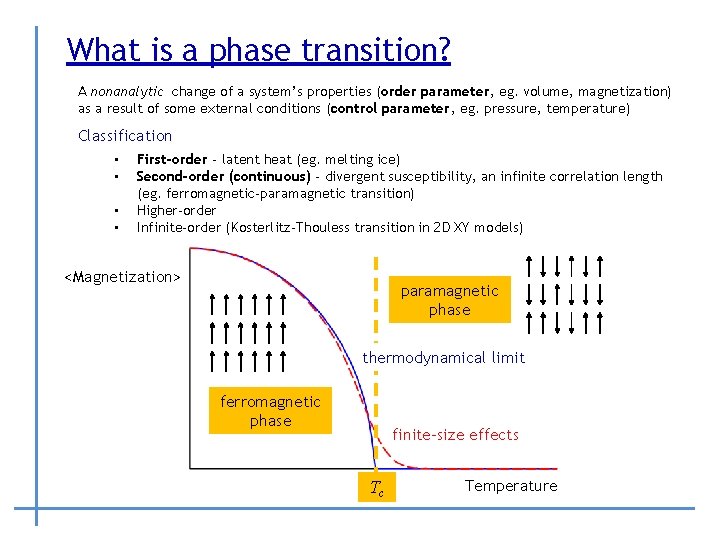
What is a phase transition? A nonanalytic change of a system’s properties (order parameter, eg. volume, magnetization) as a result of some external conditions (control parameter, eg. pressure, temperature) Classification • • First-order - latent heat (eg. melting ice) Second-order (continuous) - divergent susceptibility, an infinite correlation length (eg. ferromagnetic-paramagnetic transition) Higher-order Infinite-order (Kosterlitz-Thouless transition in 2 D XY models) <Magnetization> paramagnetic phase thermodynamical limit ferromagnetic phase finite-size effects Tc Temperature

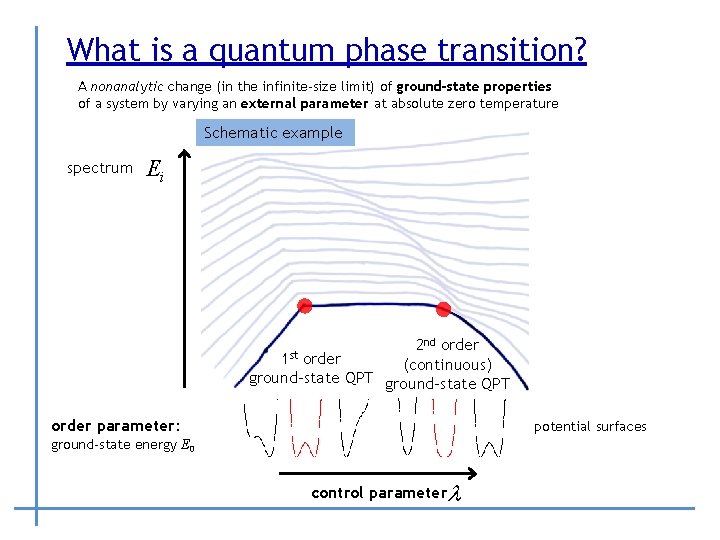
What is a quantum phase transition? A nonanalytic change (in the infinite-size limit) of ground-state properties of a system by varying an external parameter at absolute zero temperature Schematic example spectrum Ei 2 nd order (continuous) ground-state QPT 1 st order parameter: potential surfaces ground-state energy E 0 control parameterl

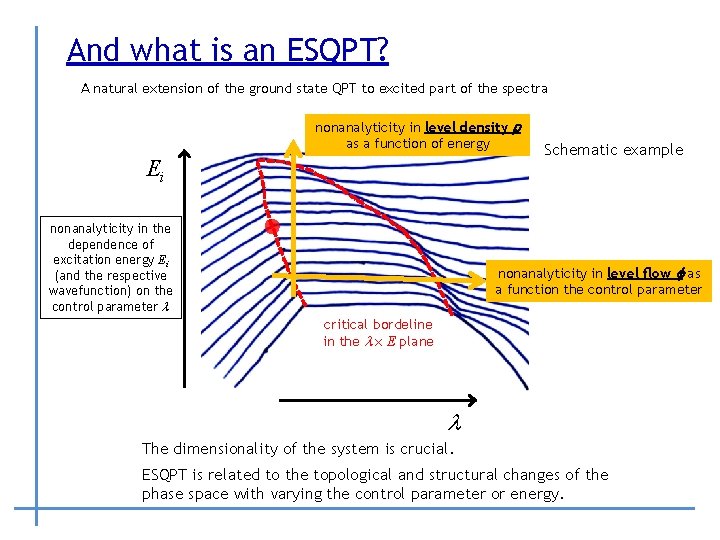
And what is an ESQPT? A natural extension of the ground state QPT to excited part of the spectra nonanalyticity in level density r as a function of energy Ei nonanalyticity in the dependence of excitation energy Ei (and the respective wavefunction) on the control parameter l Schematic example nonanalyticity in level flow f as a function the control parameter critical bordeline in the l x E plane l The dimensionality of the system is crucial. ESQPT is related to the topological and structural changes of the phase space with varying the control parameter or energy.

Finite models - size of the system - number of independent components of the system - number of degrees of freedom Nonanalyticities in phase transitions occur only when the system’s size Finite model: while f is maintained finite grows to infinity. - this limit coincides with the classical limit Generally, the number of degrees of freedom f grows with N. However, f is maintained in collective models described by some dynamical algebra A of rank r, for which • f is related with the rank r (in s & x boson models f = r - 1) • is usually related with the considered irreducible representation of the algebra In quantized classical systems, Example: Interacting Boson Model - b bosons (of the type s or d) – quasiparticles, generating a U(6) algebra (f = 5) - 3 degrees of freedom are always separated (conserving angular momentum) (index of the representation of the U(6) algebra)

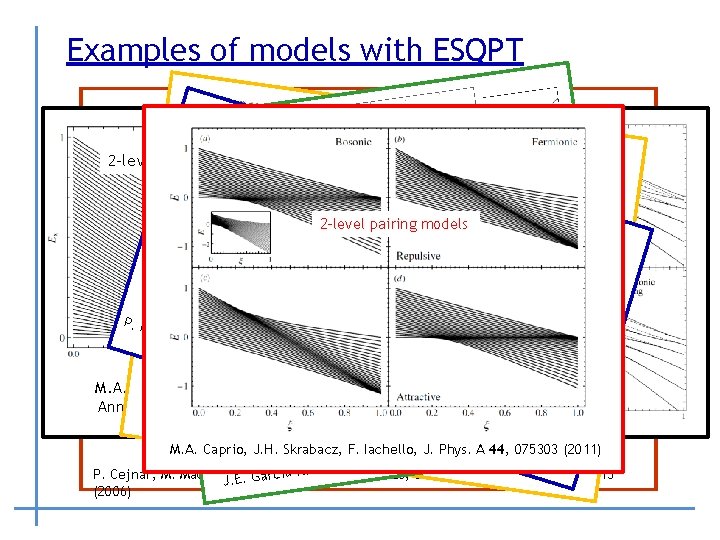
Examples of models with ESQPT O(6)-U(5) transition in the Interacting Boson Model Geometr ic collec tive model o 2 -level fermionic pairing model f atomic Lipk nuclei in m odel 2 -level pairing models P. P érez -Fer nánd ez, A . Re la Phys ño, J. M M. A. Caprio, P. Cejnar, F. . RIachello, ev. A. Arias , J 80, Annals of Physics 323, 1106 (2008) 0321. Dukels ky, J 11 ( kelsky, u D P. Cejna. J 2 , s. a 00 ) E. ri r, P. Strá A ar 3 c, ía 033802 (2009 nský, Ph P. Cejnar 9, ) J. M. G 8 -Ram (2011). Rev. E h ezy, s. Iachello, M. A. Caprio, J. H. Skrabacz, J. 8 y, s. Phys. . 0 Rev. AA 44, 075303 rnánd. F. e 7 F os, P z , e o r ñ 3 é a 1 130 (200 Rel P. P. A , s o ) Ram P. Cejnar, M. Macek, S. Heinze, Jolie, J. Dobeš, J. Phys. A: Math. 8 Gen. 39, L 515 cía-J. J. E. Gar (2006)

Hamiltonian (the form under study in this work) • Standard quadratic kinetic term • No mixing of coordinates and momenta • Potential V analytic and confining (discrete spectrum)

2. Models

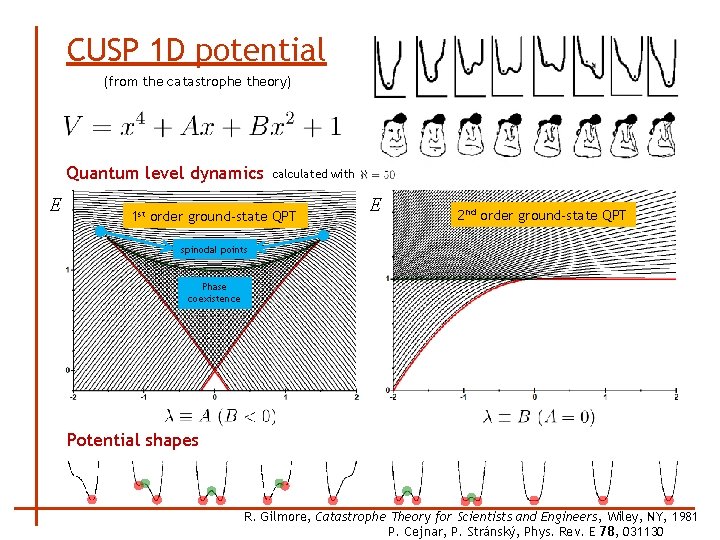
CUSP 1 D potential (from the catastrophe theory) Quantum level dynamics E calculated with 1 st order ground-state QPT E 2 nd order ground-state QPT spinodal points Phase coexistence Potential shapes R. Gilmore, Catastrophe Theory for Scientists and Engineers, Wiley, NY, 1981 P. Cejnar, P. Stránský, Phys. Rev. E 78, 031130

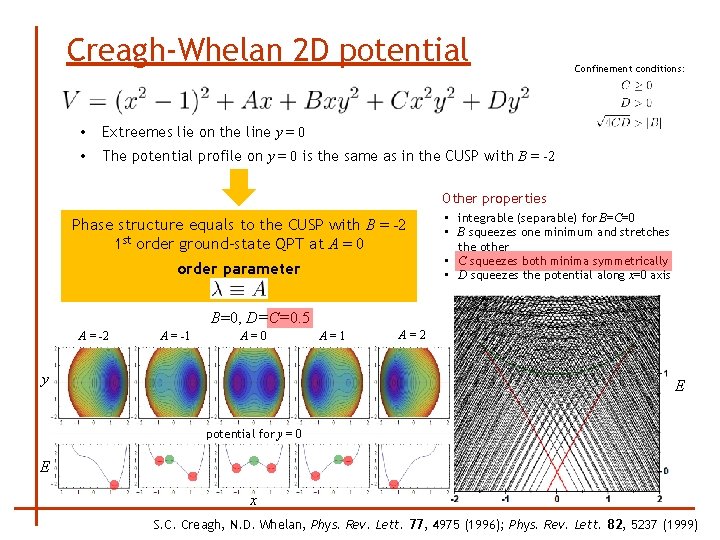
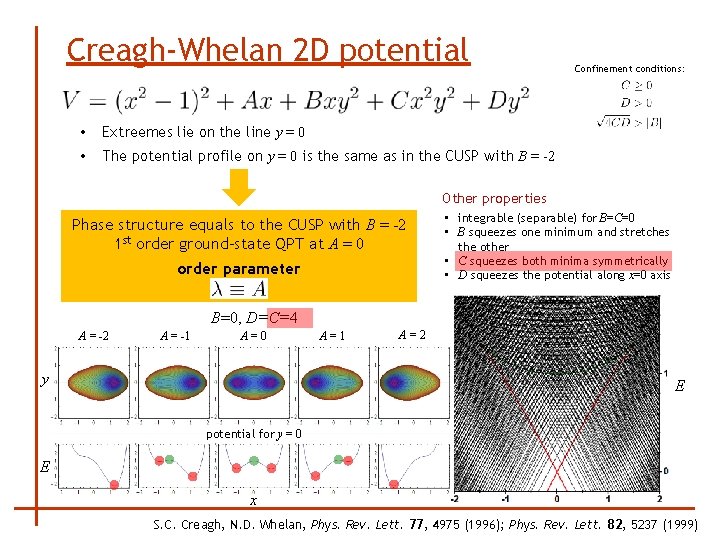
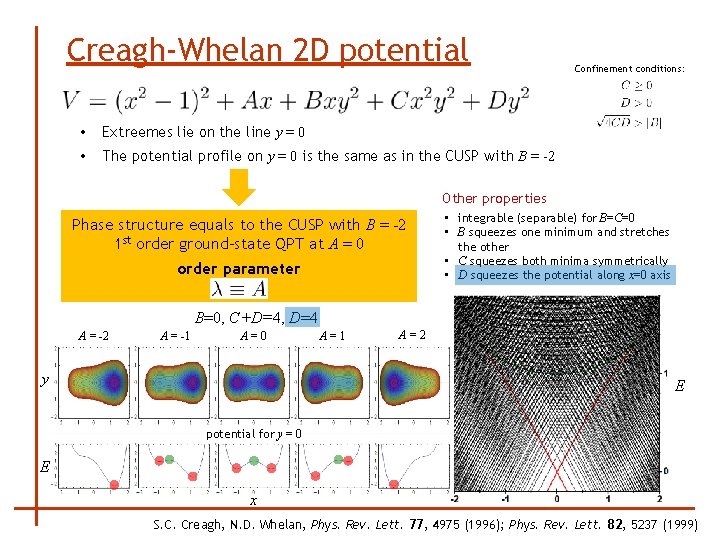
Creagh-Whelan 2 D potential • Extreemes lie on the line y = 0 • The potential profile on y = 0 is the same as in the CUSP with B = -2 Confinement conditions: Other properties Phase structure equals to the CUSP with B = -2 1 st order ground-state QPT at A = 0 order parameter • integrable (separable) for B=C=0 • B squeezes one minimum and stretches the other • C squeezes both minima symmetrically • D squeezes the potential along x=0 axis B=0, D=C=0. 5 A = -2 A = -1 A=0 y A=1 A=2 E potential for y = 0 E x S. C. Creagh, N. D. Whelan, Phys. Rev. Lett. 77, 4975 (1996); Phys. Rev. Lett. 82, 5237 (1999)

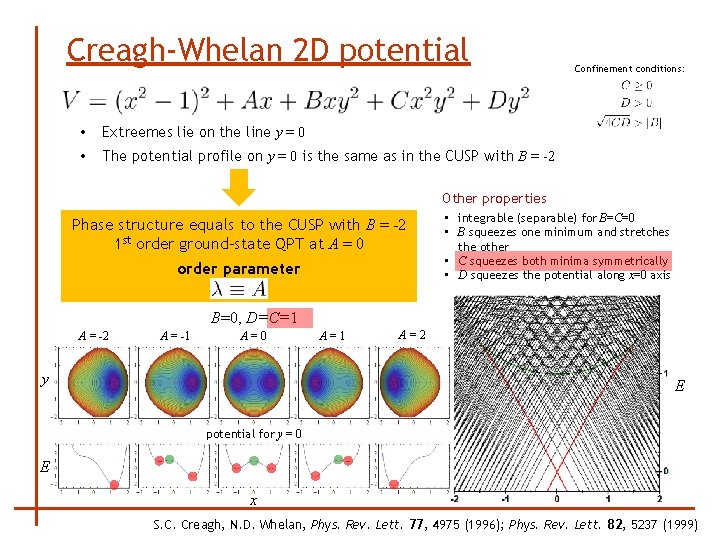
Creagh-Whelan 2 D potential • Extreemes lie on the line y = 0 • The potential profile on y = 0 is the same as in the CUSP with B = -2 Confinement conditions: Other properties Phase structure equals to the CUSP with B = -2 1 st order ground-state QPT at A = 0 order parameter • integrable (separable) for B=C=0 • B squeezes one minimum and stretches the other • C squeezes both minima symmetrically • D squeezes the potential along x=0 axis B=0, D=C=1 A = -2 A = -1 A=0 y A=1 A=2 E potential for y = 0 E x S. C. Creagh, N. D. Whelan, Phys. Rev. Lett. 77, 4975 (1996); Phys. Rev. Lett. 82, 5237 (1999)

Creagh-Whelan 2 D potential • Extreemes lie on the line y = 0 • The potential profile on y = 0 is the same as in the CUSP with B = -2 Confinement conditions: Other properties Phase structure equals to the CUSP with B = -2 1 st order ground-state QPT at A = 0 order parameter • integrable (separable) for B=C=0 • B squeezes one minimum and stretches the other • C squeezes both minima symmetrically • D squeezes the potential along x=0 axis B=0, D=C=4 A = -2 A = -1 A=0 y A=1 A=2 E potential for y = 0 E x S. C. Creagh, N. D. Whelan, Phys. Rev. Lett. 77, 4975 (1996); Phys. Rev. Lett. 82, 5237 (1999)

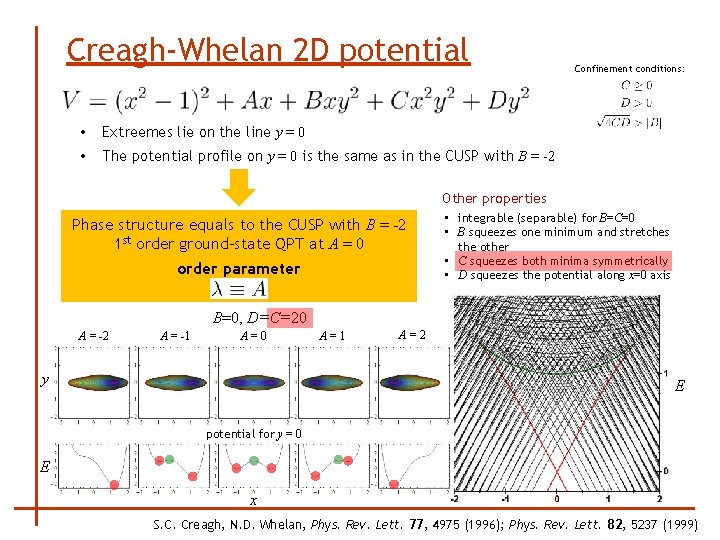
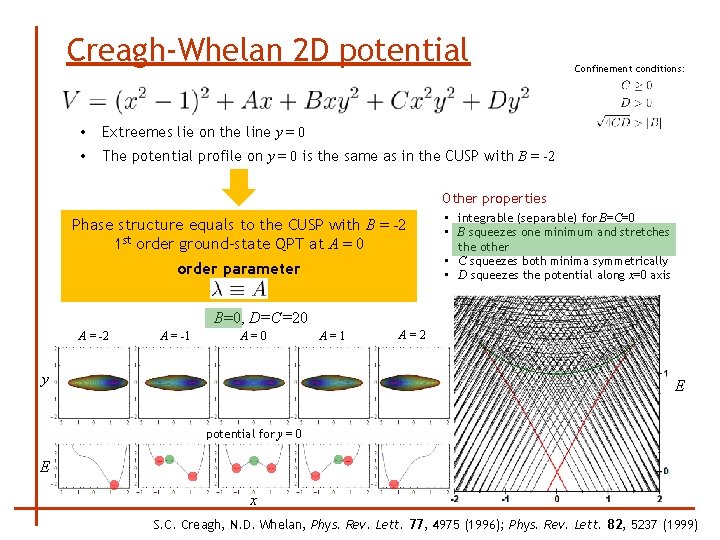
Creagh-Whelan 2 D potential • Extreemes lie on the line y = 0 • The potential profile on y = 0 is the same as in the CUSP with B = -2 Confinement conditions: Other properties Phase structure equals to the CUSP with B = -2 1 st order ground-state QPT at A = 0 order parameter • integrable (separable) for B=C=0 • B squeezes one minimum and stretches the other • C squeezes both minima symmetrically • D squeezes the potential along x=0 axis B=0, D=C=20 A = -2 A = -1 A=0 y A=1 A=2 E potential for y = 0 E x S. C. Creagh, N. D. Whelan, Phys. Rev. Lett. 77, 4975 (1996); Phys. Rev. Lett. 82, 5237 (1999)

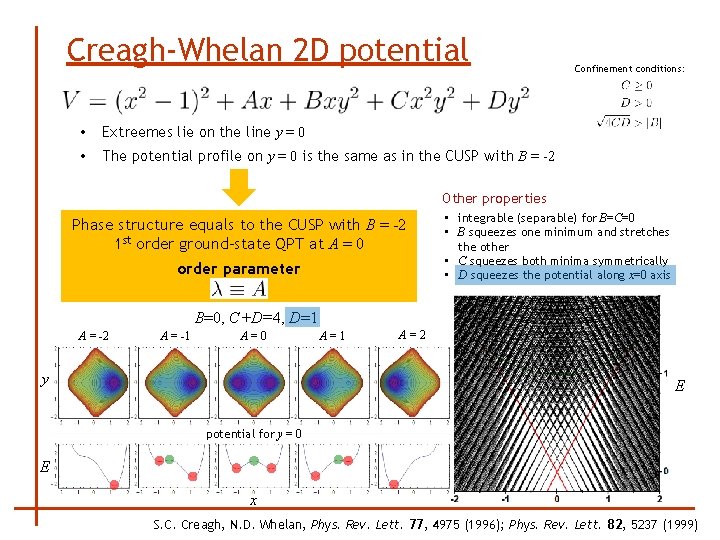
Creagh-Whelan 2 D potential • Extreemes lie on the line y = 0 • The potential profile on y = 0 is the same as in the CUSP with B = -2 Confinement conditions: Other properties Phase structure equals to the CUSP with B = -2 1 st order ground-state QPT at A = 0 order parameter • integrable (separable) for B=C=0 • B squeezes one minimum and stretches the other • C squeezes both minima symmetrically • D squeezes the potential along x=0 axis B=0, C+D=4, D=1 A = -2 A = -1 A=0 y A=1 A=2 E potential for y = 0 E x S. C. Creagh, N. D. Whelan, Phys. Rev. Lett. 77, 4975 (1996); Phys. Rev. Lett. 82, 5237 (1999)

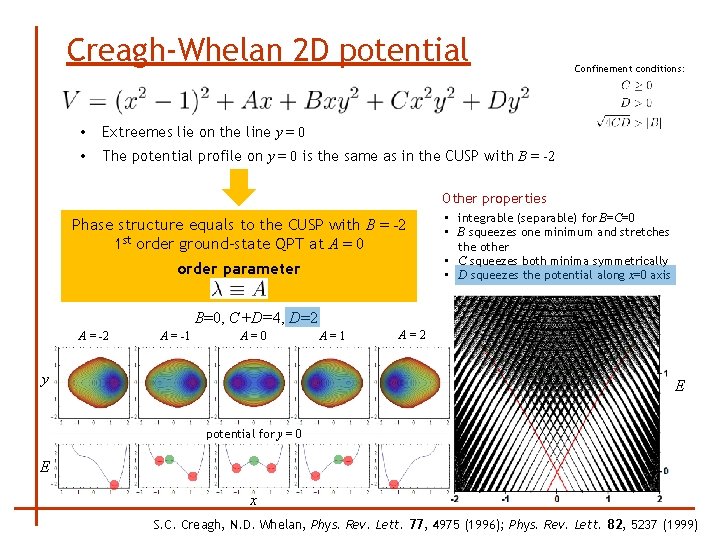
Creagh-Whelan 2 D potential • Extreemes lie on the line y = 0 • The potential profile on y = 0 is the same as in the CUSP with B = -2 Confinement conditions: Other properties Phase structure equals to the CUSP with B = -2 1 st order ground-state QPT at A = 0 order parameter • integrable (separable) for B=C=0 • B squeezes one minimum and stretches the other • C squeezes both minima symmetrically • D squeezes the potential along x=0 axis B=0, C+D=4, D=2 A = -1 A=0 y A=1 A=2 E potential for y = 0 E x S. C. Creagh, N. D. Whelan, Phys. Rev. Lett. 77, 4975 (1996); Phys. Rev. Lett. 82, 5237 (1999)

Creagh-Whelan 2 D potential • Extreemes lie on the line y = 0 • The potential profile on y = 0 is the same as in the CUSP with B = -2 Confinement conditions: Other properties Phase structure equals to the CUSP with B = -2 1 st order ground-state QPT at A = 0 order parameter • integrable (separable) for B=C=0 • B squeezes one minimum and stretches the other • C squeezes both minima symmetrically • D squeezes the potential along x=0 axis B=0, C+D=4, D=4 A = -2 A = -1 A=0 y A=1 A=2 E potential for y = 0 E x S. C. Creagh, N. D. Whelan, Phys. Rev. Lett. 77, 4975 (1996); Phys. Rev. Lett. 82, 5237 (1999)

Creagh-Whelan 2 D potential • Extreemes lie on the line y = 0 • The potential profile on y = 0 is the same as in the CUSP with B = -2 Confinement conditions: Other properties Phase structure equals to the CUSP with B = -2 1 st order ground-state QPT at A = 0 order parameter • integrable (separable) for B=C=0 • B squeezes one minimum and stretches the other • C squeezes both minima symmetrically • D squeezes the potential along x=0 axis B=0, D=C=20 A = -2 A = -1 A=0 y A=1 A=2 E potential for y = 0 E x S. C. Creagh, N. D. Whelan, Phys. Rev. Lett. 77, 4975 (1996); Phys. Rev. Lett. 82, 5237 (1999)

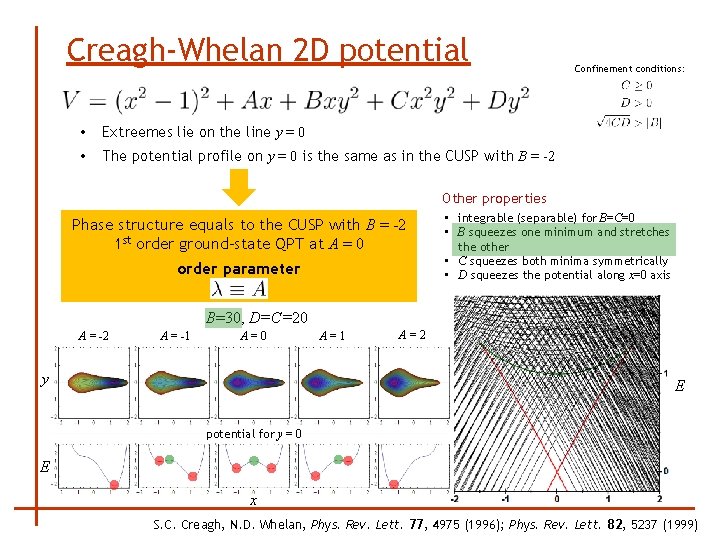
Creagh-Whelan 2 D potential • Extreemes lie on the line y = 0 • The potential profile on y = 0 is the same as in the CUSP with B = -2 Confinement conditions: Other properties Phase structure equals to the CUSP with B = -2 1 st order ground-state QPT at A = 0 order parameter • integrable (separable) for B=C=0 • B squeezes one minimum and stretches the other • C squeezes both minima symmetrically • D squeezes the potential along x=0 axis B=30, D=C=20 A = -2 A = -1 A=0 y A=1 A=2 E potential for y = 0 E x S. C. Creagh, N. D. Whelan, Phys. Rev. Lett. 77, 4975 (1996); Phys. Rev. Lett. 82, 5237 (1999)

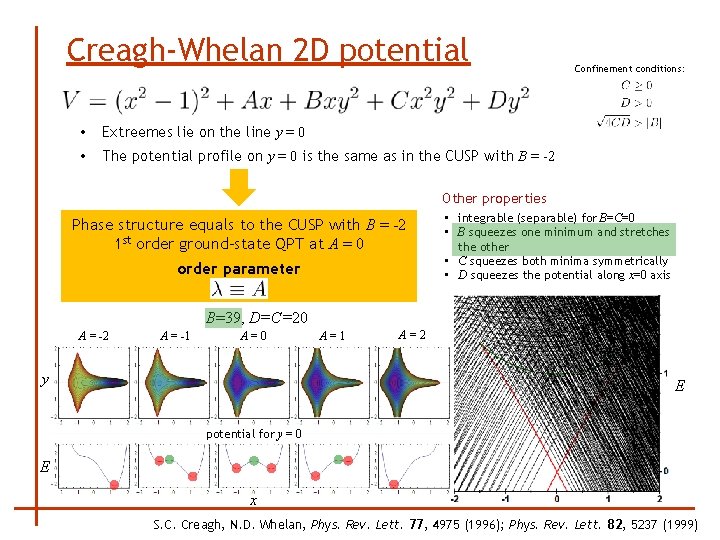
Creagh-Whelan 2 D potential • Extreemes lie on the line y = 0 • The potential profile on y = 0 is the same as in the CUSP with B = -2 Confinement conditions: Other properties Phase structure equals to the CUSP with B = -2 1 st order ground-state QPT at A = 0 order parameter • integrable (separable) for B=C=0 • B squeezes one minimum and stretches the other • C squeezes both minima symmetrically • D squeezes the potential along x=0 axis B=39, D=C=20 A = -2 A = -1 A=0 y A=1 A=2 E potential for y = 0 E x S. C. Creagh, N. D. Whelan, Phys. Rev. Lett. 77, 4975 (1996); Phys. Rev. Lett. 82, 5237 (1999)

3. Signatures of ESQPT

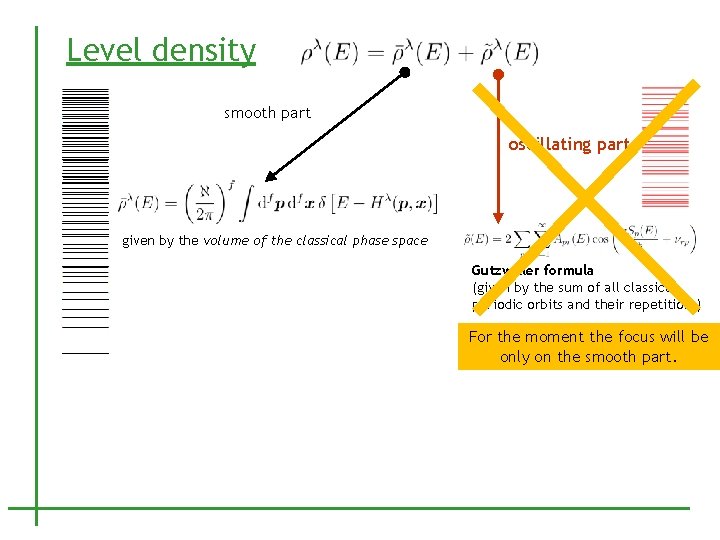
Level density smooth part oscillating part given by the volume of the classical phase space Gutzwiller formula (given by the sum of all classical periodic orbits and their repetitions) For the moment the focus will be only on the smooth part.

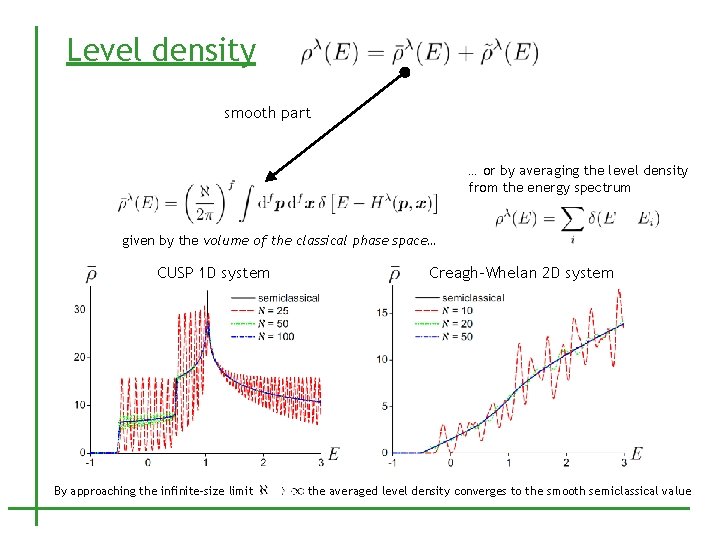
Level density smooth part … or by averaging the level density from the energy spectrum given by the volume of the classical phase space… CUSP 1 D system By approaching the infinite-size limit Creagh-Whelan 2 D system the averaged level density converges to the smooth semiclassical value

Smooth level density - integrated over momenta surface of f-dimensional sphere with unit radius Domain of the available configuration space at energy E (union of all n disjunct parts) Special cases f = 1: (sum over periods of all distinct trajectories at energy E) (derivative of the total accessible phase-space area) f = 2: (sum over the total coordinate area accessible at energy E)

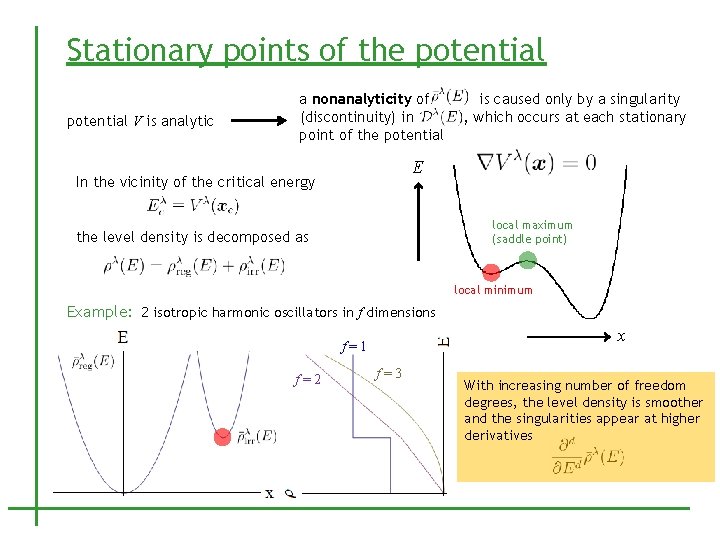
Stationary points of the potential V is analytic a nonanalyticity of (discontinuity) in point of the potential is caused only by a singularity , which occurs at each stationary E In the vicinity of the critical energy local maximum (saddle point) the level density is decomposed as local minimum Example: 2 isotropic harmonic oscillators in f dimensions x f=1 f=2 f=3 With increasing number of freedom degrees, the level density is smoother and the singularities appear at higher derivatives

Classification of singularities f = 1 1. Local minimum E local maximum local minimum x for k=4 (for quadratic minimum k = 2) In 1 D systems, a singularity always appears in the level density (jump or divergence) k = 2 (jump) infinite period of the motion on the top of the barrier - divergence 2. Local maximum k=2 (logarithmic) for k = 2 k=4

Classification of singularities f = 2 1. Local minimum (+) or maximum (-) quadratic separable isotropic k = 2 (break) isotropic minimum 2. Saddle point isotropic maximum k=l=2 k = 2, l = 3 k=4 k=2 saddles In a 2 D system, the level density is continuous; a singularity (discontinuity) appears in the first energy derivative k = 2, l = 3 k=l=2 k=4

Isotropic minimum for arbitrary f the additional well behaves locally as dxk derivatives of the level density are continuous. The more degrees of freedom, the more “analytic” the level density is. Notes: • • This conclusion holds qualitatively also for local maxima and saddle points of different types. The formula for works also for noninteger f

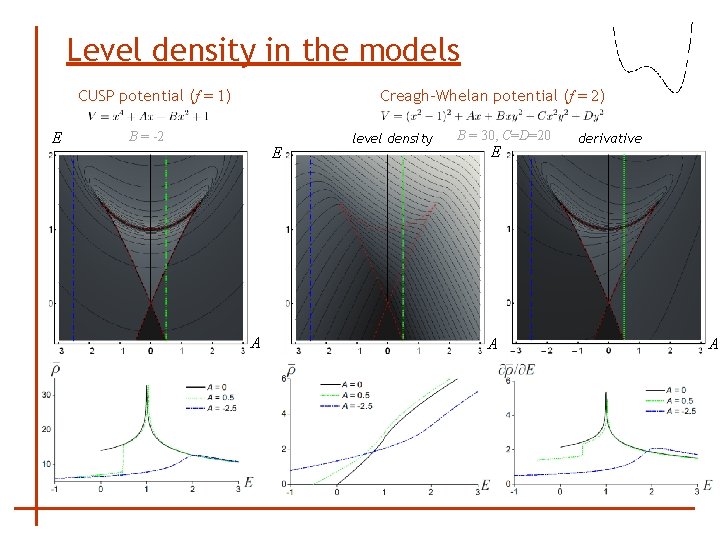
Level density in the models Creagh-Whelan potential (f = 2) CUSP potential (f = 1) E B = -2 E A level density B = 30, C=D=20 E A derivative A

Thermodynamical properties - inverse temperature canonical ensemble microcanonical ensemble smooth partition function thermal distribution usually a single-peaked function whose maximum gives the microcanonical inverse temperature: Regular and irregular temperature interested only in the irregular part caloric curve Thermal anomalies can occur when ln r is not a monotonously increasing concave function of energy.

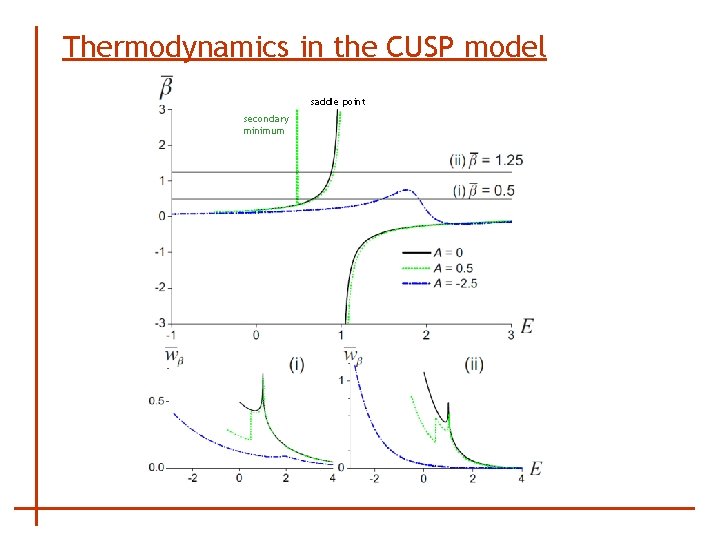
Thermodynamics in the CUSP model saddle point secondary minimum

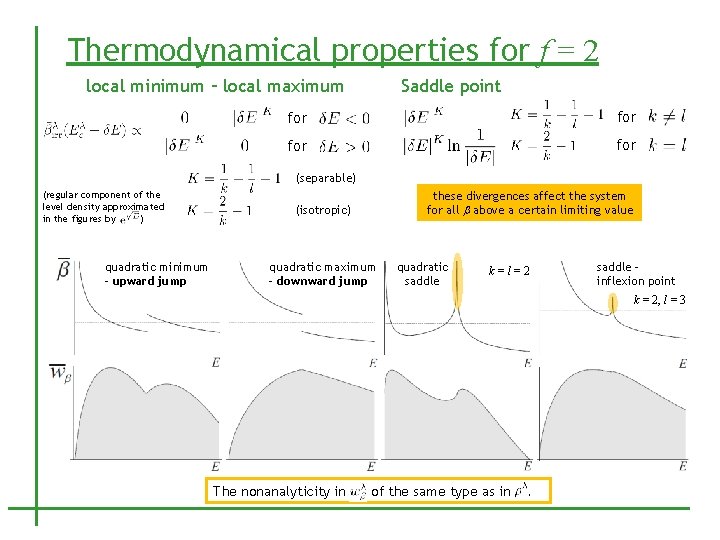
Thermodynamical properties for f = 2 local minimum – local maximum Saddle point for for (separable) (regular component of the level density approximated in the figures by ) quadratic minimum – upward jump these divergences affect the system for all b above a certain limiting value (isotropic) quadratic maximum – downward jump quadratic saddle k=l=2 saddle – inflexion point k = 2, l = 3 The nonanalyticity in of the same type as in .

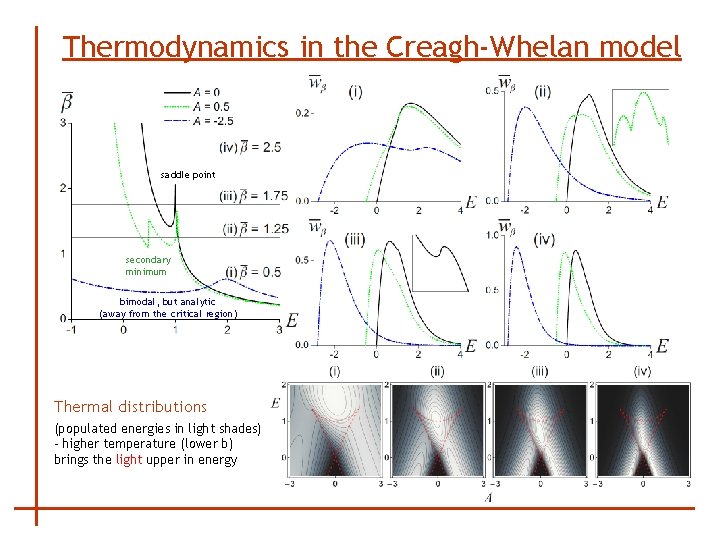
Thermodynamics in the Creagh-Whelan model saddle point secondary minimum bimodal, but analytic (away from the critical region) Thermal distributions (populated energies in light shades) - higher temperature (lower b) brings the light upper in energy

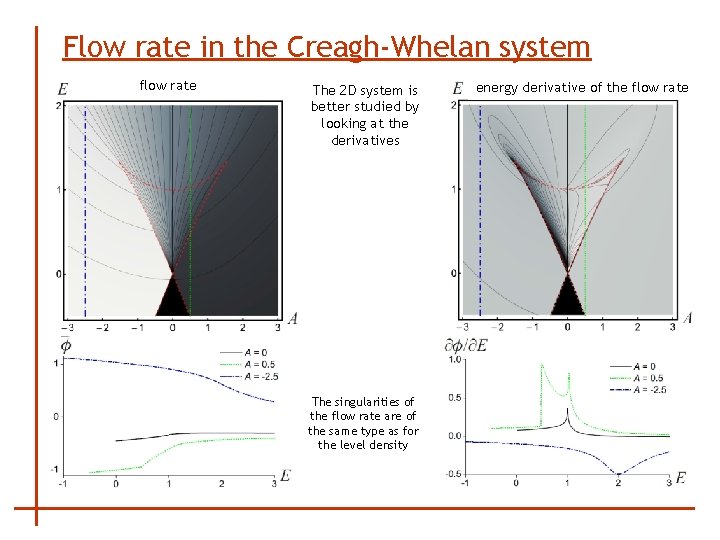
Flow rate of the spectrum - playing the role of velocity, it satisfies the Continuity equation weighted average of the expectation value of the perturbation: (connects the level density – with its singularities – and the flow rate) The flow rate can be determined by • integrating the continuity equation: • using the Hellmann-Feynman formula from the wave functions: Nonanalyticities on the critical borderline 1 opposite jump of the flow rate • f = 1: jump of level density divergence of the level density gives generally indeterminate result • f = 2: break of level density opposite break of the flow rate infinite derivative of the level density the opposite divergence of the absolute flow rate derivative In our systems and this derivative equals x

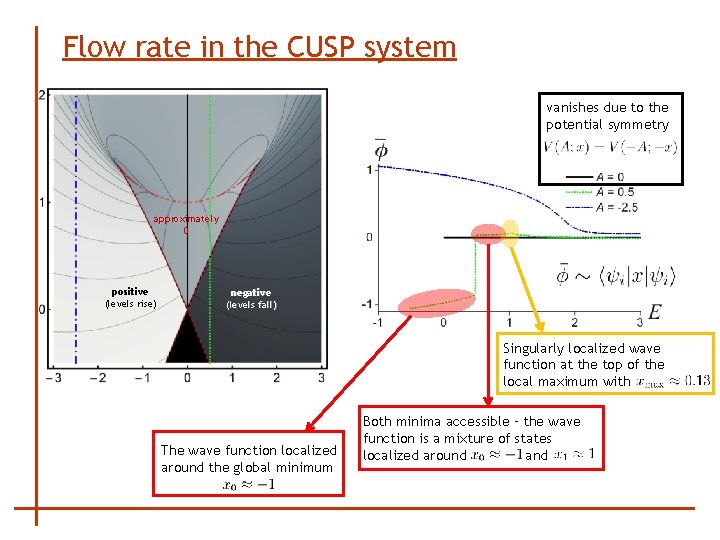
Flow rate in the CUSP system vanishes due to the potential symmetry approximately 0 positive (levels rise) negative (levels fall) Singularly localized wave function at the top of the local maximum with The wave function localized around the global minimum Both minima accessible – the wave function is a mixture of states localized around and

Flow rate in the Creagh-Whelan system flow rate The 2 D system is better studied by looking at the derivatives The singularities of the flow rate are of the same type as for the level density energy derivative of the flow rate

Conclusions • ESQPT originate in classical stationary points of the potential (local minima, maxima and saddle points) • ESQPT are presented as Singularities in the level density, - singularities in the smooth part of the level density thermal distribution function and flow rate are of the same type. - anomalies of thermodynamical properties - nonanalytic spectral flow properties with changing control parameter • ESQPT as presented are applicable to systems with finite number of degrees of freedom – models of collective dynamics of many-body systems, eg. : - f = 1 Lipkin-Meshkov-Glick model, Tavis-Cummings model - f = 2 Dicke model, Interacting boson model • The nonanalytic features of ESQPT fade quickly with increasing f Outlook • The effect of more complicated kinetic terms • Finite-size effects, multiple critical triangles • Relation of been the ESQPT with to the. Annals chaotic This work has submitted of dynamics Physics (P. Stránský, P. Cejnar, M. Macek).

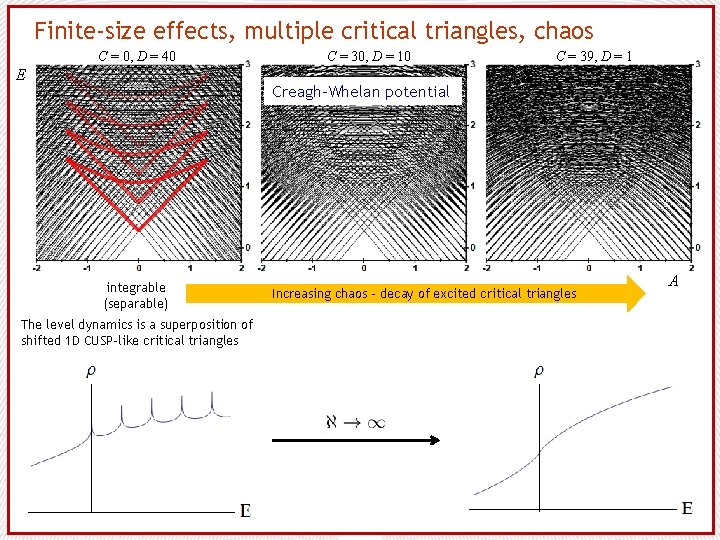
Finite-size effects, multiple critical triangles, chaos C = 0, D = 40 E C = 30, D = 10 C = 39, D = 1 Creagh-Whelan potential integrable (separable) The level dynamics is a superposition of shifted 1 D CUSP-like critical triangles Increasing chaos – decay of excited critical triangles A

Conclusions • ESQPT originate in classical stationary points of the potential (local minima, maxima and saddle points) • ESQPT are presented as Singularities in the level density, - singularities in the smooth part of the level density thermal distribution function and flow rate are of the same type. - anomalies of thermodynamical properties - nonanalytic spectral flow properties with changing control parameter • ESQPT as presented are applicable to systems with finite number of degrees of freedom – models of collective dynamics of many-body systems, eg. : - f = 1 Lipkin-Meshkov-Glick model, Tavis-Cummings model - f = 2 Dicke model, Interacting boson model • The nonanalytic features of ESQPT fade quickly with increasing f Outlook • The effect of more complicated kinetic terms • Finite-size effects, multiple critical triangles • Relation of the ESQPT with the chaotic dynamics

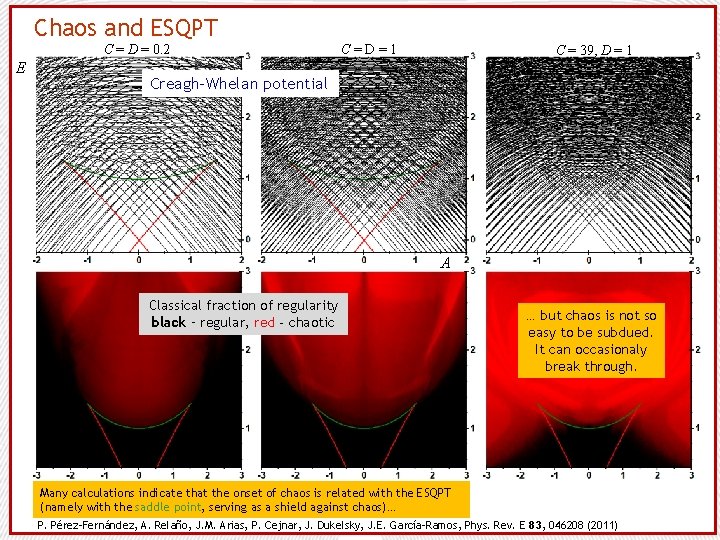
Chaos and ESQPT C = D = 0. 2 E C=D=1 C = 39, D = 1 Creagh-Whelan potential A Classical fraction of regularity black – regular, red - chaotic … but chaos is not so easy to be subdued. It can occasionaly break through. Many calculations indicate that the onset of chaos is related with the ESQPT (namely with the saddle point, serving as a shield against chaos)… P. Pérez-Fernández, A. Relaño, J. M. Arias, P. Cejnar, J. Dukelsky, J. E. García-Ramos, Phys. Rev. E 83, 046208 (2011)

Conclusions • ESQPT originate in classical stationary points of the potential (local minima, maxima and saddle points) • ESQPT are presented as Singularities in the level density, - singularities in the smooth part of the level density thermal distribution function and flow rate are of the same type. - anomalies of thermodynamical properties - nonanalytic spectral flow properties with changing control parameter • ESQPT as presented are applicable to systems with finite number of degrees of freedom – models of collective dynamics of many-body systems, eg. : - f = 1 Lipkin-Meshkov-Glick model, Tavis-Cummings model - f = 2 Dicke model, Interacting boson model • The nonanalytic features of ESQPT fade quickly with increasing f Outlook • The effect of more complicated kinetic terms • Finite-size effects, multiple critical triangles • Relation of the ESQPT with the chaotic dynamics THANK YOU FOR YOUR More images on: ATTENTION http: //www. pavelstransky. cz/cw. php

Conclusions • ESQPT originate in classical stationary points of the potential (local minima, maxima and saddle points) • ESQPT are presented as Singularities in the level density, - singularities in the smooth part of the level density thermal distribution function and flow rate are of the same type. - anomalies of thermodynamical properties - nonanalytic spectral flow properties with changing control parameter • ESQPT as presented are applicable to systems with finite number of degrees of freedom – models of collective dynamics of many-body systems, eg. : - f = 1 Lipkin-Meshkov-Glick model, Tavis-Cummings model - f = 2 Dicke model, Interacting boson model • The nonanalytic features of ESQPT fade quickly with increasing f Outlook • The effect of more complicated kinetic terms • Finite-size effects, multiple critical triangles • Relation of the ESQPT with the chaotic dynamics THANK YOU FOR YOUR More images on: ATTENTION http: //www. pavelstransky. cz/cw. php