Examples of Undecidable Problems CS 130 Theory of

Examples of Undecidable Problems CS 130 Theory of Computation HMU Textbook: Chap 9

More undecidable problems n P 1 P: print-1 problem n n Prove undecidability using diagonalization HPA: “all-inputs” halting problem n Prove undecidability using reduction

The Print-1 Problem n n The Print-1 Problem (P 1 P): Given a TM P and input i, does P leave 1 on the tape? P 1 P is undecidable That is, there is no program (turing machine) that solves P 1 P If there was such a program n n Its input will have two portions, P and i It outputs either a YES or a NO depending on whether P halts on input i, and leaves a 1 on the tape

P 1 P is undecidable n Proof by contradiction: suppose P 1 P is decidable n n Plan: arrive at a contradiction If P 1 P is decidable, then there exists a program A that solves P 1 P: P, i A YES NO

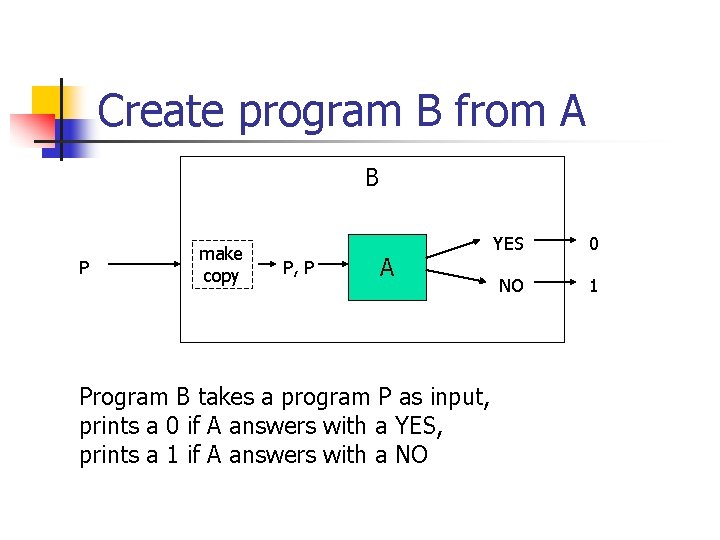
Create program B from A B P make copy P, P A Program B takes a program P as input, prints a 0 if A answers with a YES, prints a 1 if A answers with a NO YES 0 NO 1

P 1 P is undecidable n n Consider feeding program B to itself Consequence (two possibilities) n It prints a 0 n n It prints a 1 n n B on input B prints a 0 if B on input B prints a 1 a contradiction B on input B prints a 1 if B on input B does not print a 1 a contradiction Therefore the supposition cannot hold, and P 1 P is undecidable

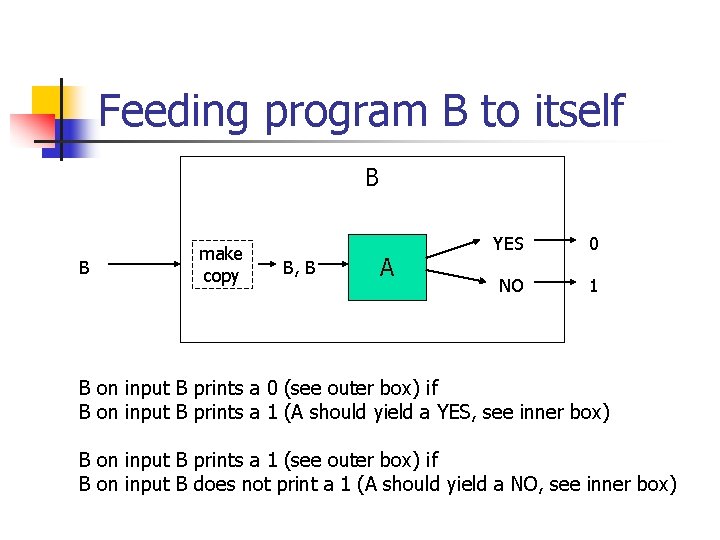
Feeding program B to itself B B make copy B, B A YES 0 NO 1 B on input B prints a 0 (see outer box) if B on input B prints a 1 (A should yield a YES, see inner box) B on input B prints a 1 (see outer box) if B on input B does not print a 1 (A should yield a NO, see inner box)

The “all-inputs” halting problem n n n The “all-inputs” Halting Problem (HPA): Given a TM P, does P halt on all inputs? This problem should be harder than HP Strategy: assume a program A that solves HPA exists, then use that program to solve HP (a contradiction, since HP is unsolvable) P A YES NO

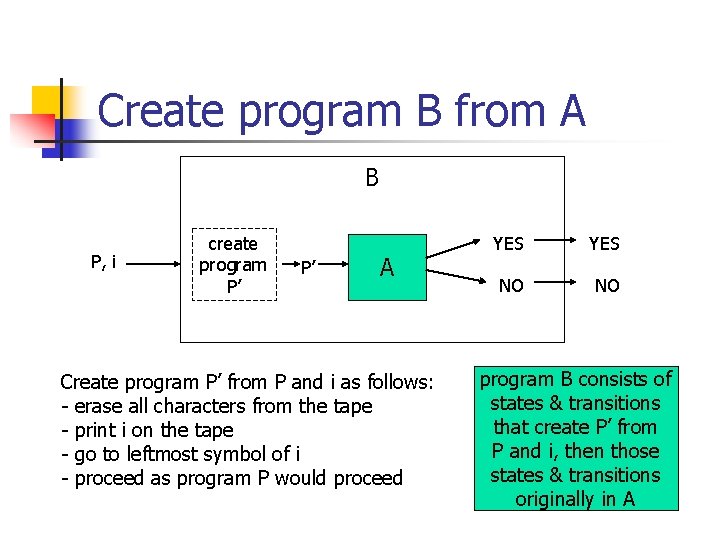
Create program B from A B P, i create program P’ P’ A Create program P’ from P and i as follows: - erase all characters from the tape - print i on the tape - go to leftmost symbol of i - proceed as program P would proceed YES NO NO program B consists of states & transitions that create P’ from P and i, then those states & transitions originally in A

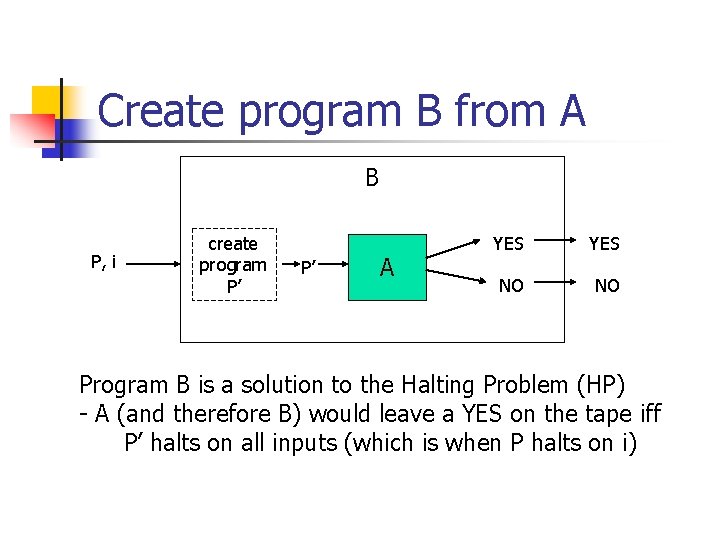
Create program B from A B P, i create program P’ P’ A YES NO NO Program B is a solution to the Halting Problem (HP) - A (and therefore B) would leave a YES on the tape iff P’ halts on all inputs (which is when P halts on i)

Undecidable problems P 1 P solvable (decidable) problems recursive context-sensitive context-free regular HPA HP

Two ways to prove undecidability n Method 1 (diagonalization) n n n Assume a program A exists that solves the problem Create a program B using A that causes a contradiction when B is fed to itself Method 2 (reduction) n n Assume a program A exists that solves the problem Create a program B from A that solves a previously known unsolvable problem (like HP), causing a contradiction