Examples of Two Dimensional Systolic Arrays Obvious Matrix

Examples of Two. Dimensional Systolic Arrays
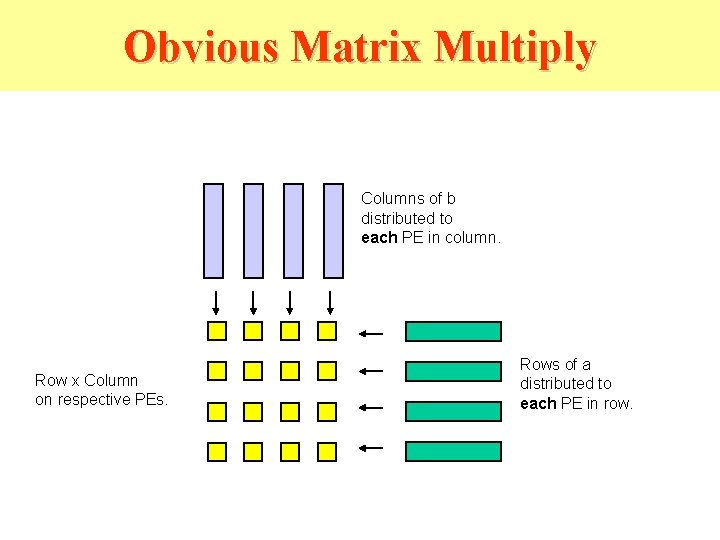
Obvious Matrix Multiply Columns of b distributed to each PE in column. Row x Column on respective PEs. Rows of a distributed to each PE in row.

Systolic Matrix Multiplication • Processors are arranged in a 2 -D grid. • Each processor accumulates one element of the product. • The elements of the matrices to be multiplied are “pumped through” the array.
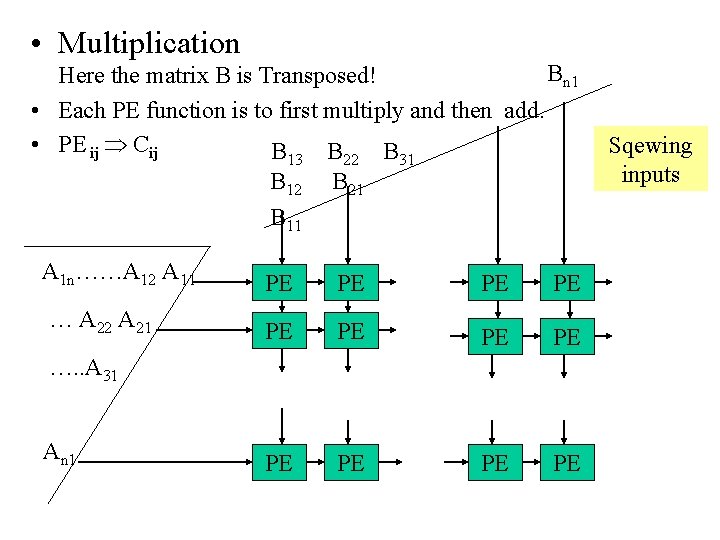
• Multiplication Bn 1 Here the matrix B is Transposed! • Each PE function is to first multiply and then add. • PE ij Cij B B B 13 A 1 n……A 12 A 11 … A 22 A 21 22 31 B 12 B 11 B 21 PE PE PE …. . A 31 An 1 Sqewing inputs
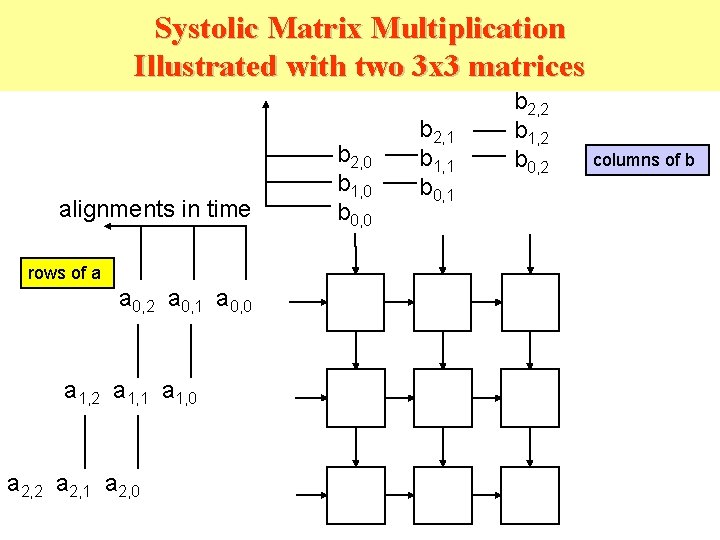
Systolic Matrix Multiplication Illustrated with two 3 x 3 matrices alignments in time rows of a a 0, 2 a 0, 1 a 0, 0 a 1, 2 a 1, 1 a 1, 0 a 2, 2 a 2, 1 a 2, 0 b 1, 0 b 0, 0 b 2, 1 b 1, 1 b 0, 1 b 2, 2 b 1, 2 b 0, 2 columns of b
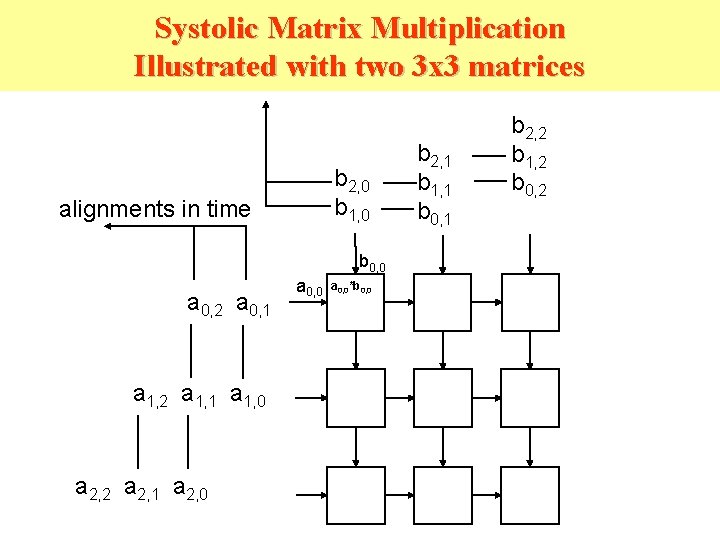
Systolic Matrix Multiplication Illustrated with two 3 x 3 matrices b 2, 0 b 1, 0 alignments in time b 0, 0 a 0, 2 a 0, 1 a 1, 2 a 1, 1 a 1, 0 a 2, 2 a 2, 1 a 2, 0 a 0, 0*b 0, 0 b 2, 1 b 1, 1 b 0, 1 b 2, 2 b 1, 2 b 0, 2
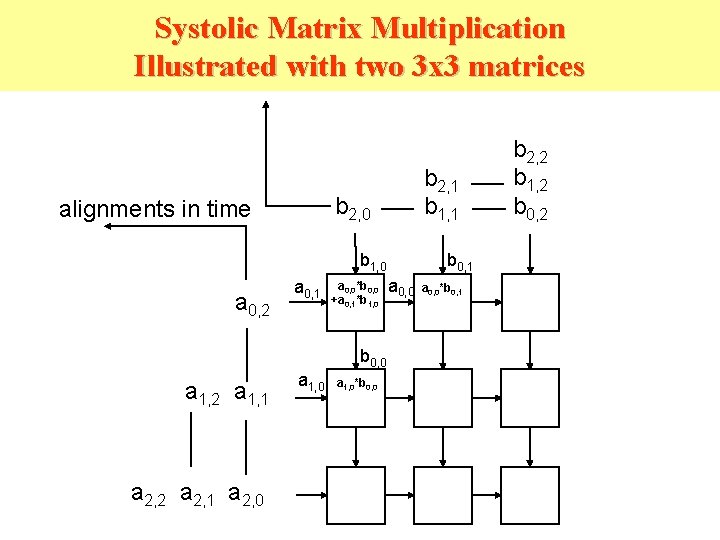
Systolic Matrix Multiplication Illustrated with two 3 x 3 matrices b 2, 1 b 1, 1 b 2, 0 alignments in time b 1, 0 a 0, 2 a 0, 1 a 0, 0*b 0, 0 +a 0, 1*b 1, 0 b 0, 0 a 1, 2 a 1, 1 a 2, 2 a 2, 1 a 2, 0 a 1, 0*b 0, 0 b 0, 1 a 0, 0*b 0, 1 b 2, 2 b 1, 2 b 0, 2
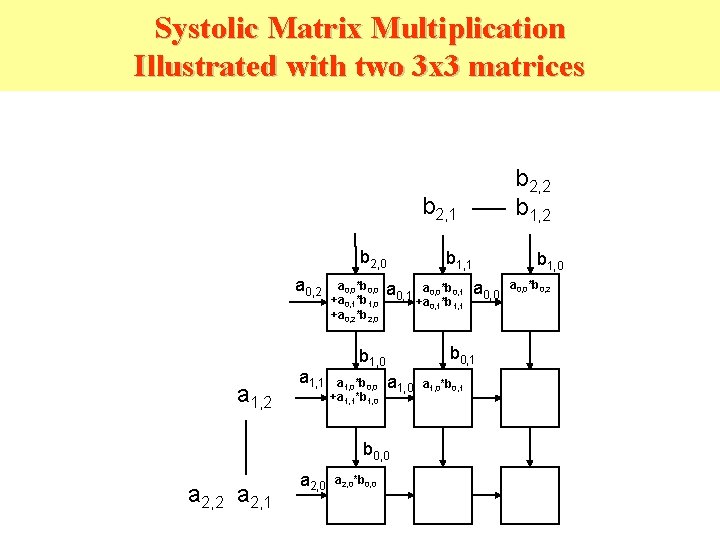
Systolic Matrix Multiplication Illustrated with two 3 x 3 matrices b 2, 2 b 1, 2 b 2, 1 b 2, 0 a 0, 2 a 1, 1 a 0, 0*b 0, 0 +a 0, 1*b 1, 0 +a 0, 2*b 2, 0 a 0, 1 a 1, 0 b 0, 0 a 2, 2 a 2, 1 a 2, 0*b 0, 0 a 0, 0*b 0, 1 +a 0, 1*b 1, 1 a 0, 0 b 0, 1 b 1, 0 a 1, 0*b 0, 0 +a 1, 1*b 1, 0 b 1, 1 a 1, 0*b 0, 1 b 1, 0 a 0, 0*b 0, 2
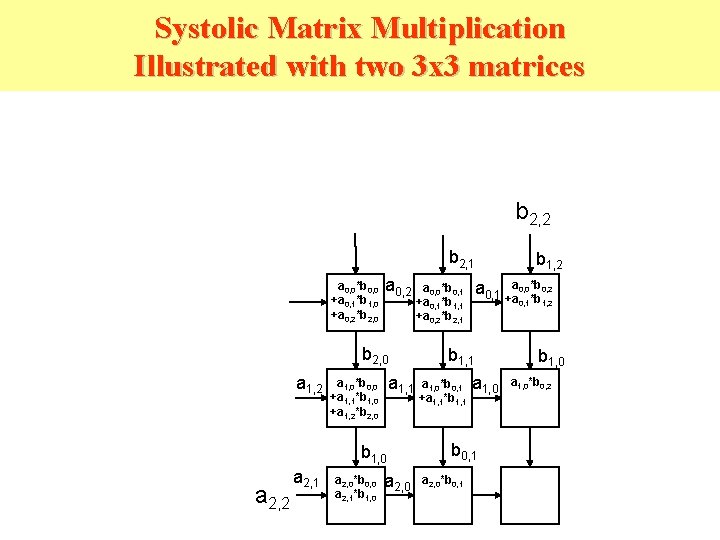
Systolic Matrix Multiplication Illustrated with two 3 x 3 matrices b 2, 2 b 2, 1 a 0, 0*b 0, 0 +a 0, 1*b 1, 0 +a 0, 2*b 2, 0 a 0, 2 b 2, 0 a 1, 2 a 1, 1 a 1, 0*b 0, 0 +a 1, 1*b 1, 0 +a 1, 2*b 2, 0 b 1, 0 a 2, 2 a 2, 1 a 2, 0*b 0, 0 a 2, 1*b 1, 0 a 2, 0 0, 2 a 0, 1 +aa 0, 0*b *b a 0, 0*b 0, 1 +a 0, 1*b 1, 1 +a 0, 2*b 2, 1 0, 1 b 1, 1 a 1, 0*b 0, 1 +a 1, 1*b 1, 1 a 1, 0 b 0, 1 a 2, 0*b 0, 1 b 1, 2 b 1, 0 a 1, 0*b 0, 2
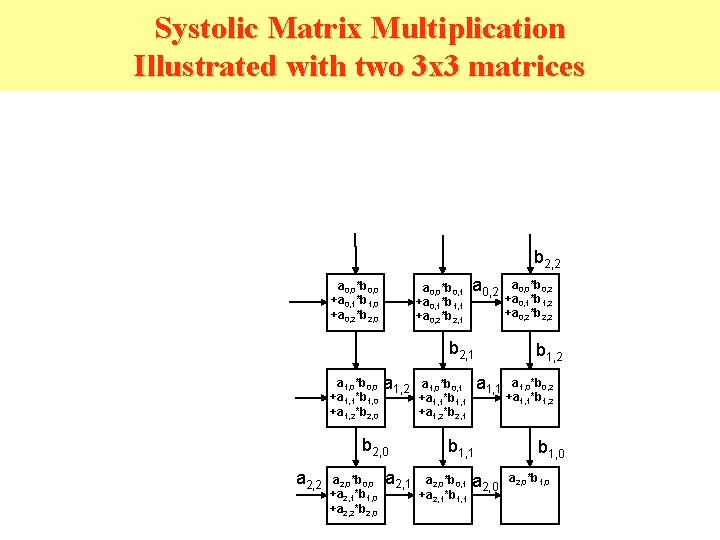
Systolic Matrix Multiplication Illustrated with two 3 x 3 matrices b 2, 2 a 0, 0*b 0, 0 +a 0, 1*b 1, 0 +a 0, 2*b 2, 0 a 0, 0*b 0, 1 +a 0, 1*b 1, 1 +a 0, 2*b 2, 1 a 0, 2 b 2, 1 a 1, 0*b 0, 0 +a 1, 1*b 1, 0 +a 1, 2*b 2, 0 a 1, 2 b 2, 0 a 2, 2 a 2, 0*b 0, 0 +a 2, 1*b 1, 0 +a 2, 2*b 2, 0 a 2, 1 b 1, 2 a 1, 1 a 1, 0*b 0, 1 +a 1, 1*b 1, 1 +a 1, 2*b 2, 1 b 1, 1 a 2, 0*b 0, 1 +a 2, 1*b 1, 1 a 0, 0*b 0, 2 +a 0, 1*b 1, 2 +a 0, 2*b 2, 2 a 2, 0 a 1, 0*b 0, 2 +a 1, 1*b 1, 2 b 1, 0 a 2, 0*b 1, 0

Systolic Matrix Multiplication Illustrated with two 3 x 3 matrices a 0, 0*b 0, 0 +a 0, 1*b 1, 0 +a 0, 2*b 2, 0 a 0, 0*b 0, 2 +a 0, 1*b 1, 2 +a 0, 2*b 2, 2 a 0, 0*b 0, 1 +a 0, 1*b 1, 1 +a 0, 2*b 2, 1 b 2, 2 a 1, 0*b 0, 0 +a 1, 1*b 1, 0 +a 1, 2*b 2, 0 a 1, 0*b 0, 1 +a 1, 1*b 1, 1 +a 1, 2*b 2, 1 a 1, 2 b 2, 1 a 2, 0*b 0, 0 +a 2, 1*b 1, 0 +a 2, 2*b 2, 0 a 2, 2 a 2, 0*b 0, 1 +a 2, 1*b 1, 1 +a 2, 2*b 2, 1 a 1, 0*b 0, 2 +a 1, 1*b 1, 2 +a 1, 2*b 2, 2 b 1, 2 a 2, 0*b 1, 0 +a 2, 0*b 1, 1
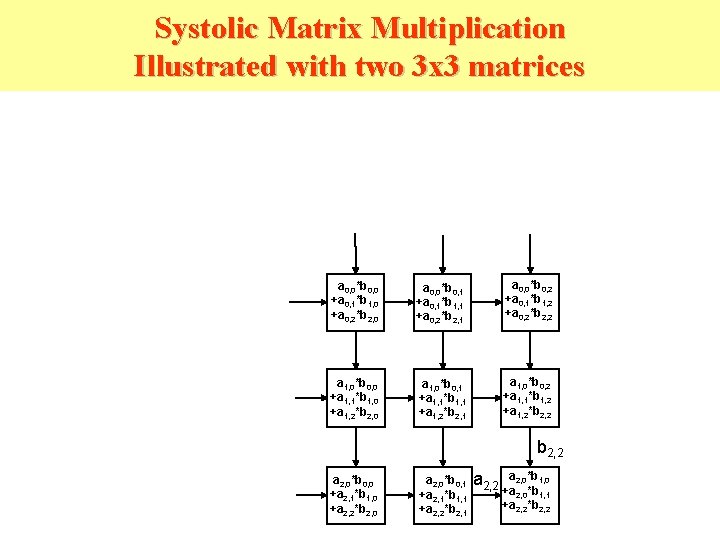
Systolic Matrix Multiplication Illustrated with two 3 x 3 matrices a 0, 0*b 0, 0 +a 0, 1*b 1, 0 +a 0, 2*b 2, 0 a 0, 0*b 0, 1 +a 0, 1*b 1, 1 +a 0, 2*b 2, 1 a 0, 0*b 0, 2 +a 0, 1*b 1, 2 +a 0, 2*b 2, 2 a 1, 0*b 0, 0 +a 1, 1*b 1, 0 +a 1, 2*b 2, 0 a 1, 0*b 0, 1 +a 1, 1*b 1, 1 +a 1, 2*b 2, 1 a 1, 0*b 0, 2 +a 1, 1*b 1, 2 +a 1, 2*b 2, 2 a 2, 0*b 0, 0 +a 2, 1*b 1, 0 +a 2, 2*b 2, 0 a 2, 0*b 0, 1 +a 2, 1*b 1, 1 +a 2, 2*b 2, 1 a 2, 2 a 2, 0*b 1, 0 +a 2, 0*b 1, 1 +a 2, 2*b 2, 2
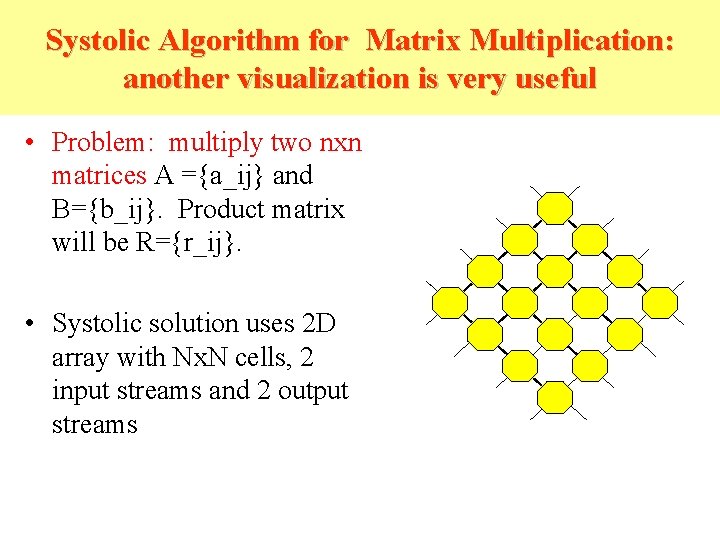
Systolic Algorithm for Matrix Multiplication: another visualization is very useful • Problem: multiply two nxn matrices A ={a_ij} and B={b_ij}. Product matrix will be R={r_ij}. • Systolic solution uses 2 D array with Nx. N cells, 2 input streams and 2 output streams
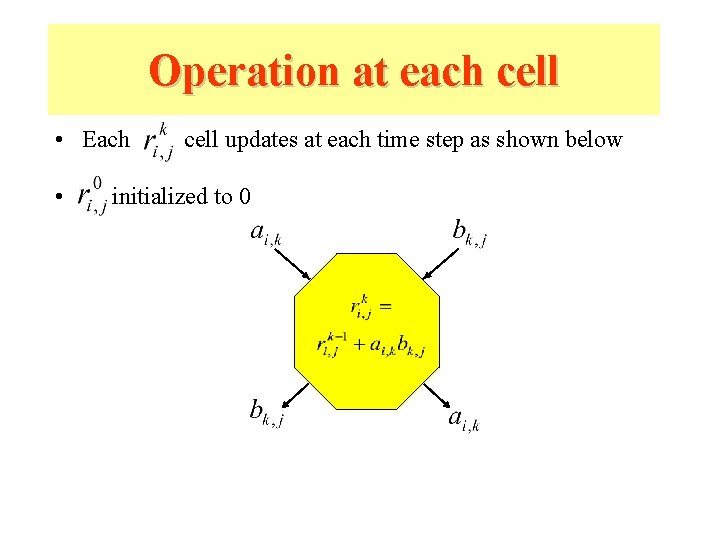
Operation at each cell • Each • cell updates at each time step as shown below initialized to 0
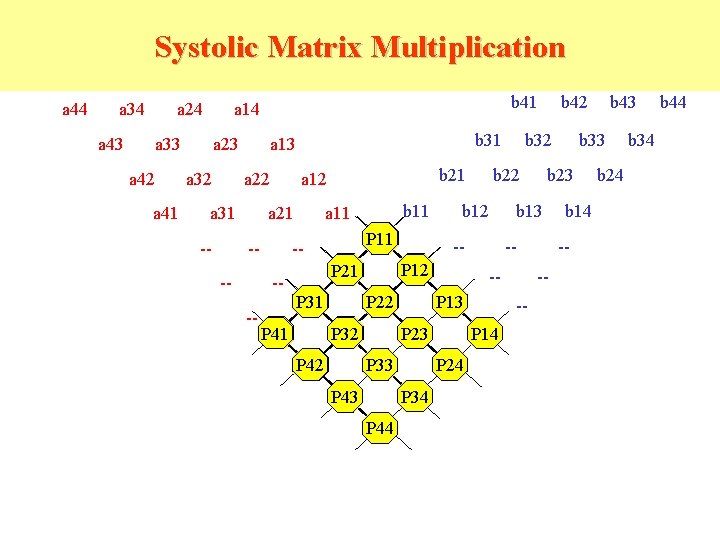
Systolic Matrix Multiplication a 44 a 34 a 24 a 43 a 14 == a 33 a 42 a 41 a 23 a 32 a 13 == a 22 a 31 -- == --- b 21 b 11 a 11 P 11 -- P 32 P 41 -P 13 P 24 P 34 P 43 P 44 b 14 -- --- P 14 P 23 P 33 P 42 -- b 43 b 33 b 23 b 13 -- P 22 b 42 b 32 b 22 b 12 P 21 P 31 b 31 == a 12 === a 21 b 41 == b 24 b 34 b 44
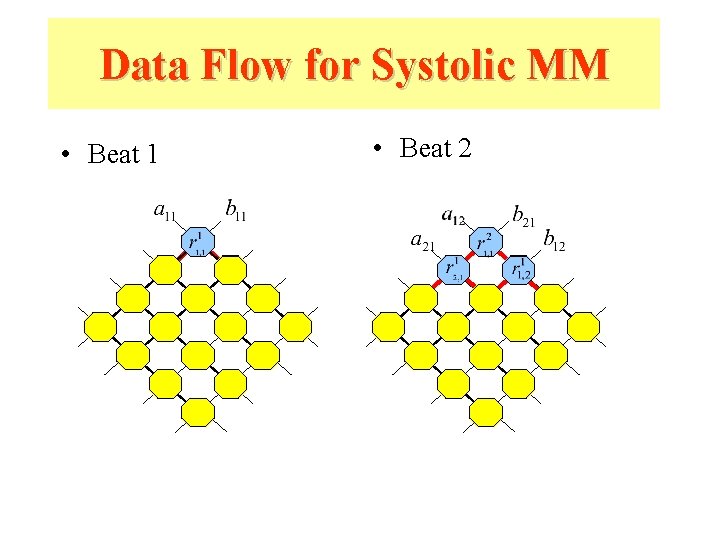
Data Flow for Systolic MM • Beat 1 • Beat 2
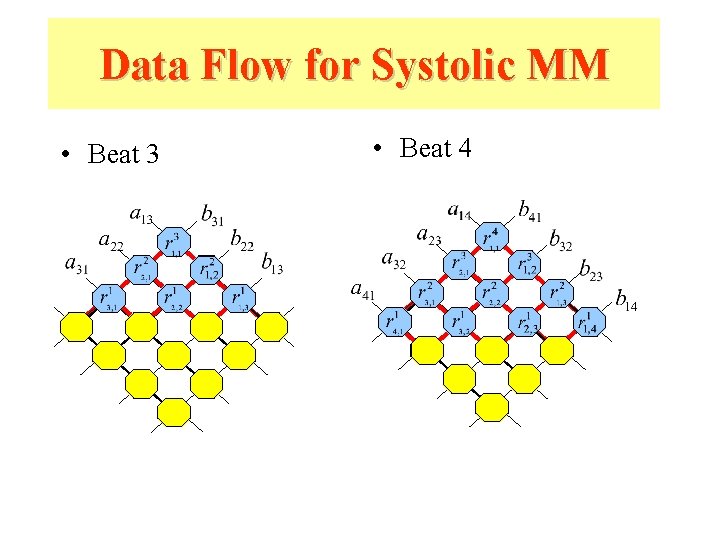
Data Flow for Systolic MM • Beat 3 • Beat 4
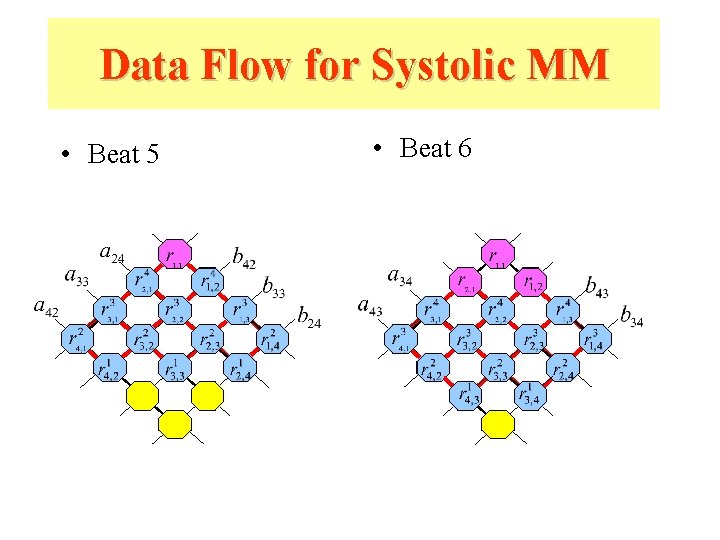
Data Flow for Systolic MM • Beat 5 • Beat 6
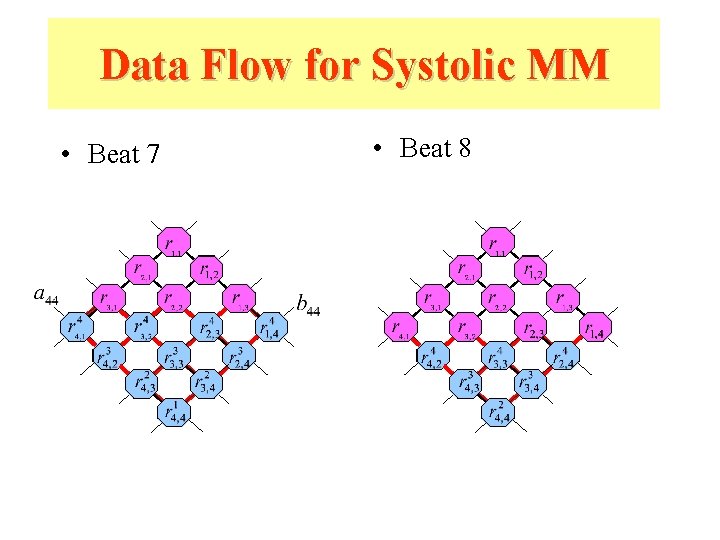
Data Flow for Systolic MM • Beat 7 • Beat 8
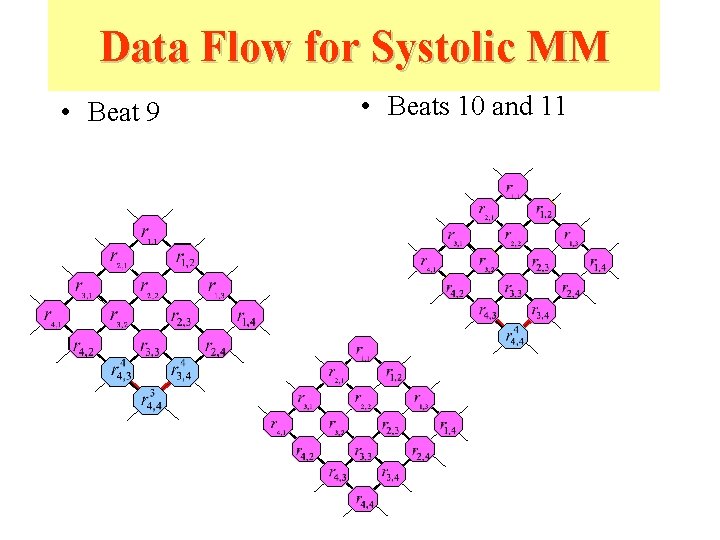
Data Flow for Systolic MM • Beat 9 • Beats 10 and 11

Programming Issues • Performance of systolic algorithms based on fine granularity (1 update about the same as a communication) and regular dataflow – Can be done on asynchronous platforms with tagging but must ensure that idle time does not dominate computation • Many systolic algorithms do not map well to more general MIMD or distributed platforms
- Slides: 21