Examples of the Question Formulation Technique QFT in





















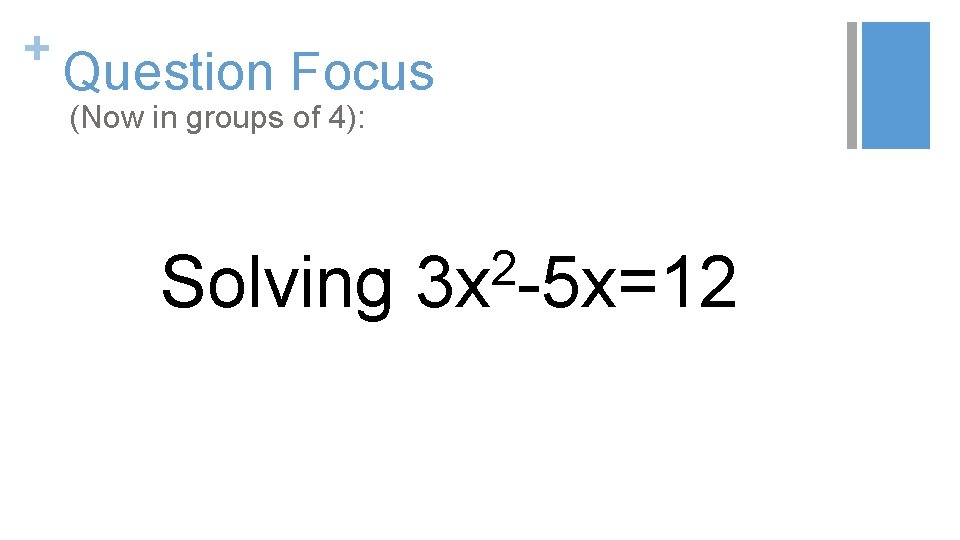





















- Slides: 49

Examples of the Question Formulation Technique (QFT) in the Math Classroom rightquestion. org

Math Examples

+ Classroom Examples: Table of Contents § § § 4 th grade, Variables 4 th grade, Composite numbers 5 th grade, Common Core word problem High School, Algebra I, Expressions & equations High school, Algebra II & III, Types of graphs High School, Algebra I, Methods for solving quadratic functions High school, Geometry, Scale factor High school, Geometry, Equations High School, Algebra I, Quadratics High School, Algebra I, Number Systems High School, Statistics, PBL: statistical research QFocus ideas § § Engaging hooks Integers Decimals, fractions, & exponents Factoring, statistics, & word problems

+ Classroom Example: 4 th Grade Teacher: Deirdre Brotherson, Hooksett, NH Topic: Math unit on variables Purpose: To engage students at the start of a unit on variables

+ Question Focus 24 = ☺ + ☺

+ Student Questions 1. 2. 3. 4. 5. 6. 7. 8. 9. Why is the 24 first? What do the smiley faces mean? Why are there 3 smiley faces? How am I suppose to figure this out? Is the answer 12? Can I put any number for a smiley face? Do three faces mean something? Do the numbers have to be the same because the smiley faces are the same? What numbers will work here? 10. 11. 12. 13. 14. 15. Does it mean 24 is a really happy number? Can we replace each smiley face with an 8? Do any other numbers work? Can we do this for any number? Does it always have to be smiley faces? Do we always have to use three things?

+ Next Steps with Student Questions ❖ Questions posted on classroom walls. ❖ Students cross off the questions they answer during subsequent lessons. ❖ Teacher returns to student questions at the end of the unit to discuss with students what they learned and what they still want to know.

+ Classroom Example: 4 th Grade Teacher: Alyssa Park, Gardnerville, NV Topic: Composite Numbers Purpose: To build number awareness skills and practice a strategy for difficult multiplication problems Back to Table of Contents

+ Question Focus Image Source: https: //twitter. com/Miss. Park. SES/status/927373487412412417

+ Student Questions ■ ■ ■ ■ How many blocks are there? Why are there black lines? Why are there 60 blue cubes and 23 orange ones? Is the problem adding and if it is why is it addition? What do orange and blue represent? Are they connected? Why is it a cube instead of numbers?

+ Classroom Example: 5 th Grade Teacher: Deirdre Brotherson, Hookset, NH Topic: Common Core Math Problem Purpose: To develop critical thinking skills in preparation for problem-solving and state testing Back to Table of Contents

+ Question Focus A Common Core Word Problem

+ Student Questions Initial Questions 1. 2. 3. 4. 5. 6. What are we supposed to do? Why are all the answers the same? What does “down” mean? Why do some have -30? What do the ( ) and [ ] mean? Do we -30 or +30? 7. What is a discount? 8. What is ½ of a balance? 9. What is a balance?

+ Student Questions Post-Vocabulary Discussion 1. Do we look at the problems with only -30? 2. Do we cross out +30 problems? 3. Do we do 110 + 30 first? 4. If we do 110 + 30 that is the amount he put down and the discount, right? 5. So that means we take that away from the total $350, right? 6. So the ( ) mean we do that first but how do we subtract that from 350 then divide by half? 7. Is that what the [ ] means?

+ Classroom Example: Algebra I Teacher: Jessica Brewer, Booneville, KY Topic: Expressions & Equations Purpose: To uncover students’ prior knowledge and develop essential questions Back to Table of Contents

+ Question Focus Image Source: https: //twitter. com/jessicabrewer 04/status/1033062227383906310

+ Student Questions 1. What is the pattern? 2. Do the letters go farther than E? 3. Does the letter equal the # it is in the alphabet? 4. If so, does B + D + E = K? 5. How do you solve the equation? 6. What if the letters add up to a # larger than 26? 7. How can you add three or more letters? 8. Are the letters used to represent #’s? 9. How do you add B + D + E together? 10. What would A + B + D+ E be? 11. How do you solve this? 12. How do you add letters? 13. What are the values of the letters? 14. What formula is used?

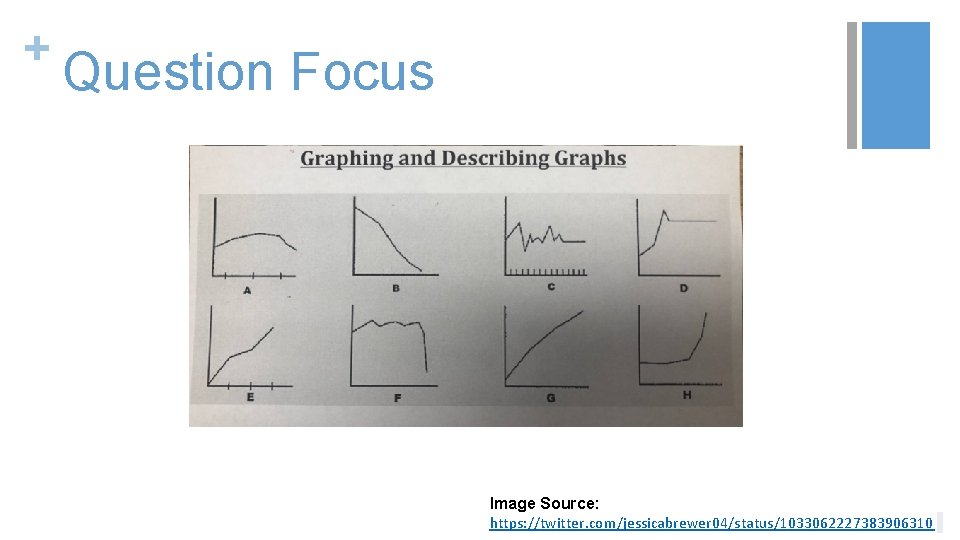
+ Classroom Example: Algebra II & III Teacher: Jessica Brewer, Booneville, KY Topic: Graphing Purpose: To discover different types of graphs and practice describing them Back to Table of Contents

+ Question Focus Image Source: https: //twitter. com/jessicabrewer 04/status/1033062227383906310

+ Combined Student Questions Algebra II: 1. 2. 3. 4. Why do some graphs have “notches”? 5. 6. 7. 8. 9. 10. Is graph A linear? If so, how? 13. 14. 15. 16. 17. 18. 19. Why are there huge falls? How do you determine the slope in graph C? How do you determine if slope is increasing or decreasing? Why is graph D going up? What are the graphs based off of? How do you know what to graph? What are the graphs describing? Where are the points located if they were plotted? 11. What do these graphs have to do with the QFT? 12. How do you describe a graph? What were the graphs for? What are the slopes of the graphs? Why does graph F look so “sad”? Why do all the lines look so different? How do you know where to plot? How is this important? Why are they labelled A, B, C, D? Algebra III: 1. 2. 3. 4. 5. Why do some graphs have tick marks? 6. What is unique to each graph? What do the graphs represent? How can graphs help gather evidence? Why does graph C fluctuate so much? Why does graph D increase, decrease, then stay steady?

+ Classroom Example: High School Teacher: Claire Yablong, Phoenix, AZ Topic: Methods for solving quadratic functions Purpose: § To reveal what students did not know or understand about the topic after students overall performed poorly on a quiz § For students to think metacognitively about their own understanding of the topic Back to Table of Contents

+ Before the Question Focus Part 1: § Students tried solving an equation, individually: 3 x 2 -5 x=12 Part 2: § Students solved the same equation with a partner, using a method not used by them or their partner on part 1.
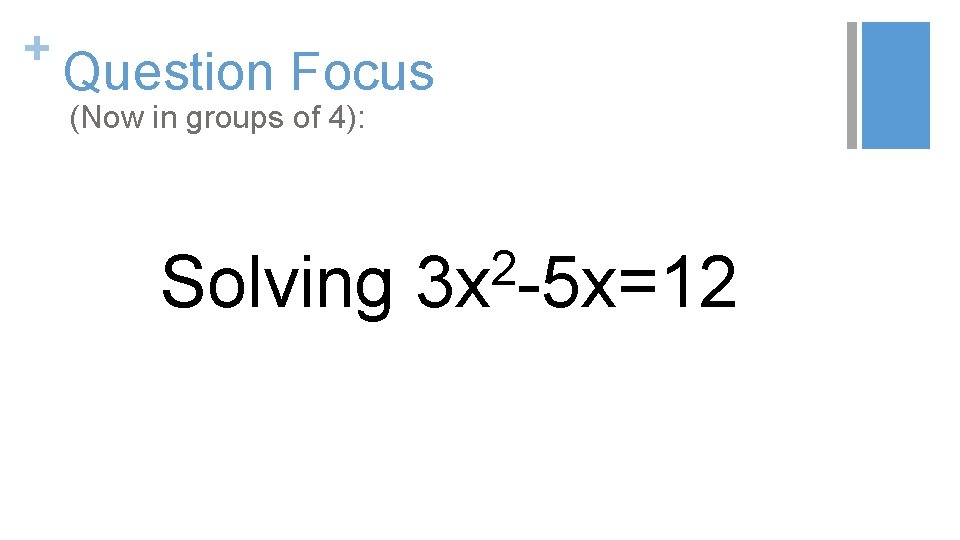
+ Question Focus (Now in groups of 4): 2 Solving 3 x -5 x=12

+ Student Questions One group’s questions: 1. Which method is easiest? 2. How would one know what is the best question to use on a question by question basis? 3. How do you check if your answer is wrong? 4. Would it affect the problem if you got a negative symbol mixed up? 5. Which way is the most difficult? 6. Which way has the smallest margin of error? 7. Why does graphing have the least amount of steps? 8. Does it matter if the answer is in fraction or decimal form? 9. Is graphing easier just because its the last step?

+ Through Asking Questions, Students… Identified gaps in their prior knowledge § How do you factor with two X’s? § What is completing the square? Made connections to prior knowledge § What does rate of change have to do with this lesson? Used mathematical reasoning § Would it change the answer if you converted to a decimal in the middle of solving? Thought metacognitively about approach and tools for solving § § How do you know if the equations is solvable? Do certain formulas work better for certain problems? Is it safe to use mental math? Is using the calculator smart for this problem? Sought a conceptual understanding § Why do we set the equation to zero? § Why are there two answers? § Why don’t you have to find the square root for factoring? Sought to extend their knowledge § What if there is no y intercept? What if it’s just 3 x^2 for example? § What are the types of equations in which it will cross the y axis? Had a place to begin § What step do you start with?

+ Next Steps with Student Questions § After answering their priority questions in groups, students then took a test on the same topic (solving methods for quadratic functions) § Students made a noticeable improvement in their scores from when they took the quiz § The teacher noted: “I think our QFT day forced some of them to stop saying ‘I don't get this’ and instead get specific about what they didn't understand. ”

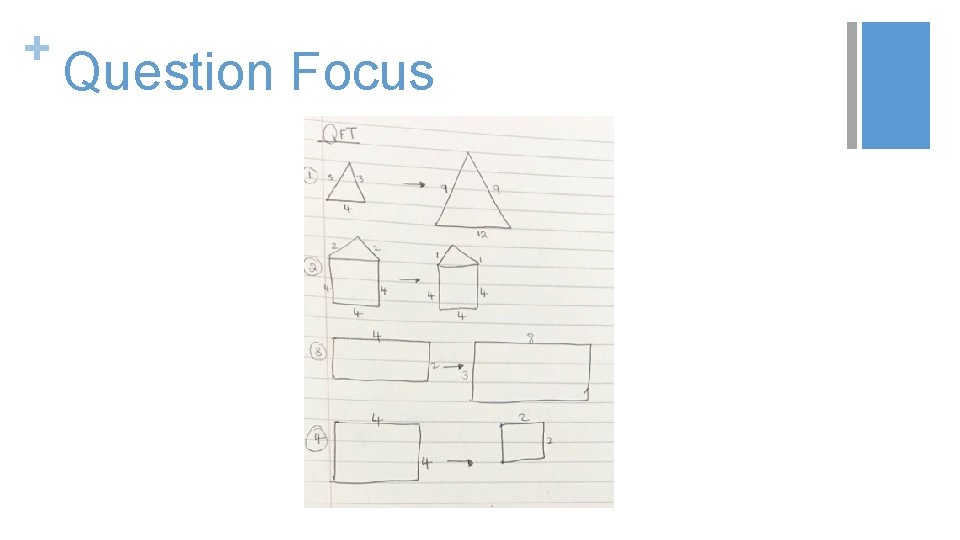
+ Classroom Example: High School Teacher: Laura Barzottini, Cape Town, South Africa Topic: Geometry Purpose: To introduce the concept of transforming shapes using a scale factor Back to Table of Contents

+ Question Focus

+ Student Questions ■ ■ Why are these 2 triangulars not the same and why are the numbers not the same? ■ Are the shapes similar or congruent? ■ Why are some small and some big? ■ Are first shapes reflections? Why are these shape the same and numbers are not the same? ■ Why is the other rectangular small and the other is big? ■ Why the cubes only have 2 numbers only?

+ Classroom Example: High School Teacher: George Marenco, Sacramento, CA Topic: Geometry Purpose: To develop essential questions for the unit on equations Back to Table of Contents

+ Question Focus Equation = Balance

+ Student Questions 1. 2. 3. 4. 5. 6. 7. 8. 9. How do you get an equation to balance? Why does an equation have to be balanced? Why does it have to be an equation? What’s the difference between equation and 10. balance? 11. Why are we supposed to know this? Does this have to do with “PEMA”? 12. Why is there an equal sign between the words? 13. Does it have to be an equation? 14. Are we supposed to know this? What is an equation? What is balance? What steps do you use to get an “equation” to “balance”? How do we find balance? What’s the answer to this problem? 15. Will we ever see this in the future?

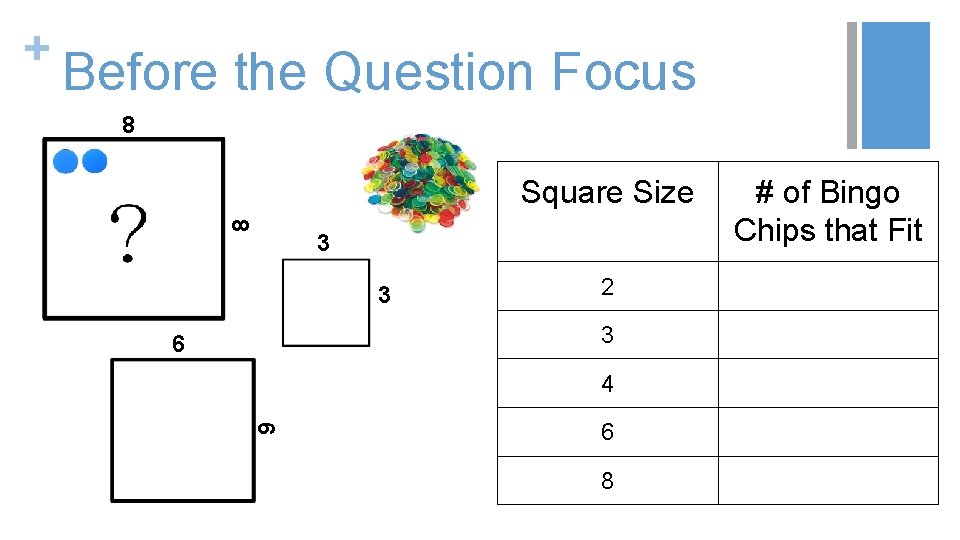
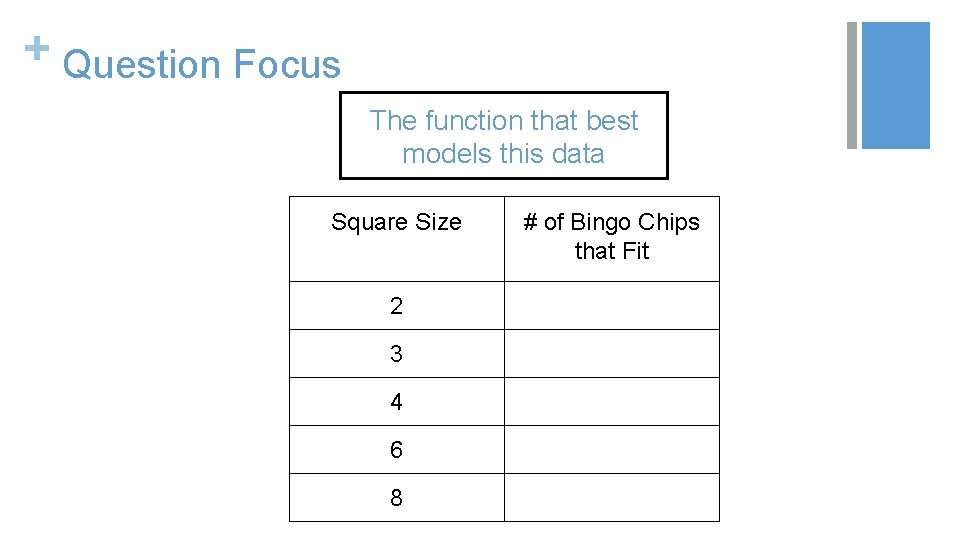
+ Classroom Example: High School Teacher: Rick Barlow, San Jose, CA Topic: Algebra 1: Quadratics Purpose: To introduce the quadratics unit by having students collect sets of data and explore using a function to model them. Back to Table of Contents

+ Before the Question Focus 8 Square Size 8 3 3 2 3 6 4 6 6 8 # of Bingo Chips that Fit

+ Question Focus The function that best models this data Square Size 2 3 4 6 8 # of Bingo Chips that Fit

+ Student Questions 1. 2. 3. 4. 5. 6. 7. Is this related to polynomial? What would you call a function that is neither linear or exponential? Will this graph give us the exact # of 8. Why does it increase rapidly then slow down? how many chips will fit in the 9. What would the slope look like? square? 10. What type of function is the graph if it Does size of chips matter? is not a J, L, or linear? Can it be exponential on a graph 11. If we were to find the amount of chips and not on a table? Why is the line on the graph curved found in an 11 in a square could we double that and find the answer for a 22 and then out of nowhere it goes inch square? straight? How could you find what the table is 12. Does the graph cross zero? 13. What kind of math did people use to multiplying by? get these solutions?

+ Next Steps with Student Questions ❖ ❖ Questions used as opening slides for the next day’s lesson Revisited at the end as a debrief

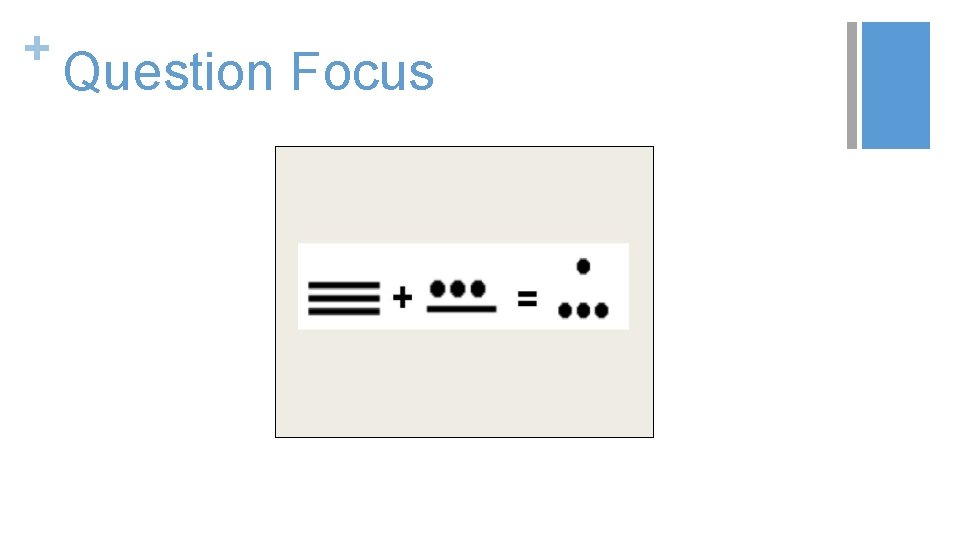
+ Classroom Example: High School Teacher: Rick Barlow, San Jose, CA Topic: Number Systems Purpose: To engage students on the first day of school; to practice backward reasoning and problem-solving skills Back to Table of Contents

+ Question Focus

+ Student Questions 1. What do the dots means? 2. What do the lines mean? 3. How do the values of the dots and lines form the equation? 4. How do you answer this equation? 5. Can you create lines using dots? 6. Why are the circles on top of the line? 7. Why are there no lines in the outcome? 8. Why is the outcome 4 circles? 9. Are they important? 10. Why is one circle higher in the outcome?

+ Next Steps with Student Questions v. Students thought of numbers that would be too high and too low for the teacher’s age. v. Students used the ideas generated by their questions to guess the teacher’s age. v. Teacher revealed the code.

+ Classroom Example: High School Teacher: Rick Barlow, San Jose, CA Topic: Immigration Statistics PBL Purpose: To produce questions for statistical research Back to Table of Contents

+ Question Focus 3 claims about immigration pulled from a campaign speech video

+ Next Steps with Student Questions ❖ Ss categorize questions as groups share: DACA, the wall, security, drugs/crime ❖ Ss’ preferences of the 4 big topics used to create groups ❖ Groups craft “claim” about topic counter to the president’s claim ❖ Ss support their claim using statistical research

For more information on Rick Barlow’s lesson ELL Students Use Statistics to Challenge Immigration Claims http: //kindlingfires. blogspot. com/2018/01/immigration-projectlaunch. html If you search the blog, you’ll find several of Rick’s QFT lessons with all levels of students—from ELL immersion classes to AP classes.

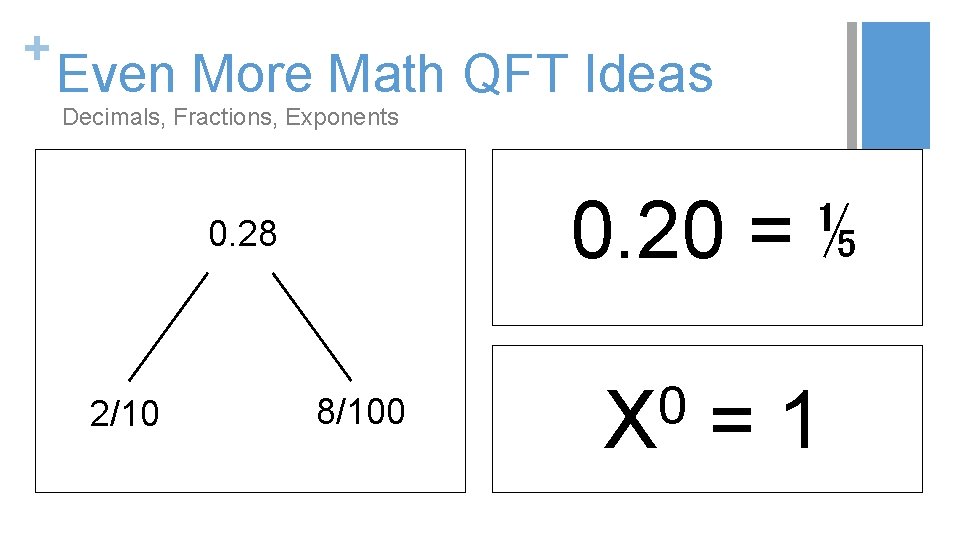
+ Even More Math QFT Ideas In the following slides, we’ve collected examples of interesting math QFocus prompts that do not have the full classroom application. Dan Meyer’s 3 -Act Math Problems Tap. Into. Teen. Minds. com A picture of three Macy’s certificates: One card that offers 15% off on a purchase, another that offers 20% off on one item, and another that offers $25 on purchases over $100. (or some other combination) Back to Table of Contents

+ Even More Math QFT Ideas Working with Integers “Broken-Egg Problem” “. . . When she put the eggs in groups of two, three, four, five, and six, there was one egg left over, but when she put them in groups of seven they ended up in complete groups with no eggs left over. ” What number leaves a remainder of 4 when divided by 7, 5 when divided by 8, and 6 when divided by 9?

+ Even More Math QFT Ideas Decimals, Fractions, Exponents 0. 20 = ⅕ 0. 28 2/10 8/100 0 X = 1

+ Even More Math QFT Ideas Quadratics, Word Problems, Statistics, Data Impossible to solve Introducing the need for factoring to solve quadratics Statistics always tell the truth Give a relatively simple problem to solve→ QFT on the answer→ Each student takes one question to individually work on further→ Present solutions, pick one, and repeat the process Correlation implies causation