Examples of singleslit diffraction Correction The figure on

Examples of single-slit diffraction (Correction !!) • The figure on the left is a photograph of a Fraunhofer pattern of a single horizontal slit. What features are especially notable ? • Example 36. 1: You pass 633 -nm light through a narrow slit and observe the diffraction pattern on a screen 6. 0 m away. The distance at the screen between the center and the first minima on either side is 32 mm long. How wide is the slit? Copyright © 2012 Pearson Education Inc.

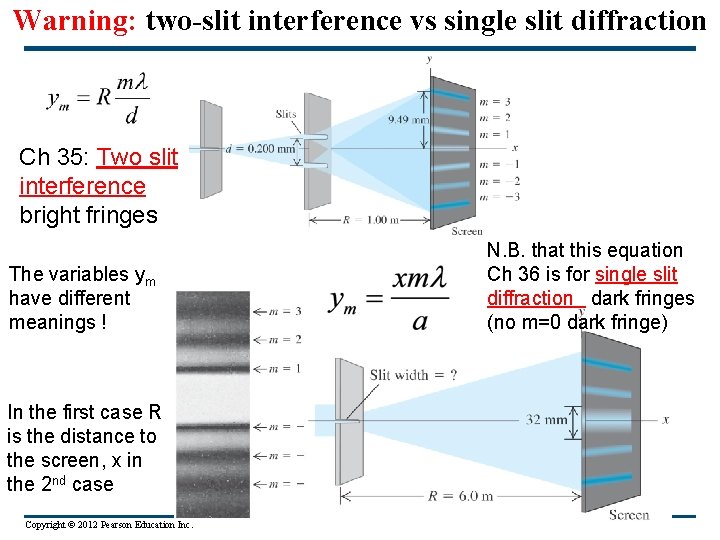
Warning: two-slit interference vs single slit diffraction Ch 35: Two slit interference bright fringes The variables ym have different meanings ! In the first case R is the distance to the screen, x in the 2 nd case Copyright © 2012 Pearson Education Inc. N. B. that this equation Ch 36 is for single slit diffraction dark fringes (no m=0 dark fringe)

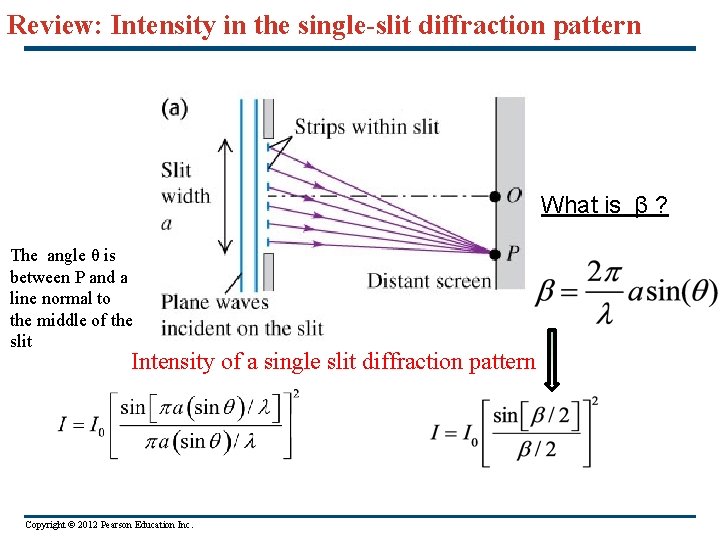
Review: Intensity in the single-slit diffraction pattern What is β ? The angle θ is between P and a line normal to the middle of the slit Intensity of a single slit diffraction pattern Copyright © 2012 Pearson Education Inc.

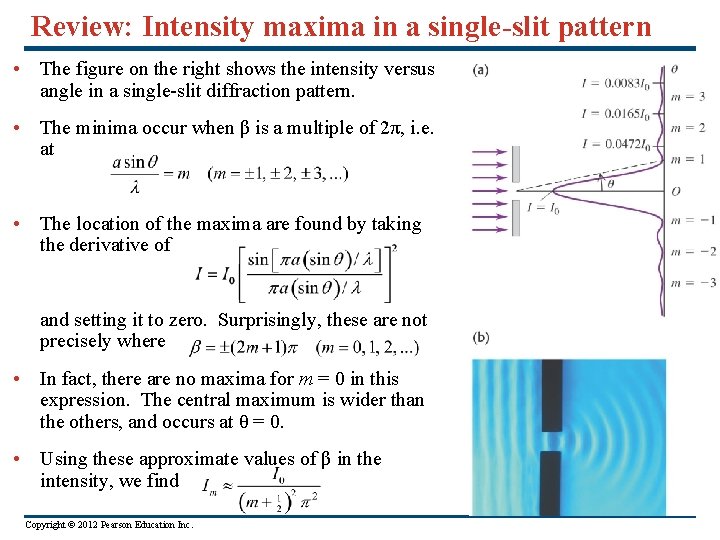
Review: Intensity maxima in a single-slit pattern • The figure on the right shows the intensity versus angle in a single-slit diffraction pattern. • The minima occur when β is a multiple of 2π, i. e. at • The location of the maxima are found by taking the derivative of and setting it to zero. Surprisingly, these are not precisely where • In fact, there are no maxima for m = 0 in this expression. The central maximum is wider than the others, and occurs at θ = 0. • Using these approximate values of β in the intensity, we find Copyright © 2012 Pearson Education Inc.

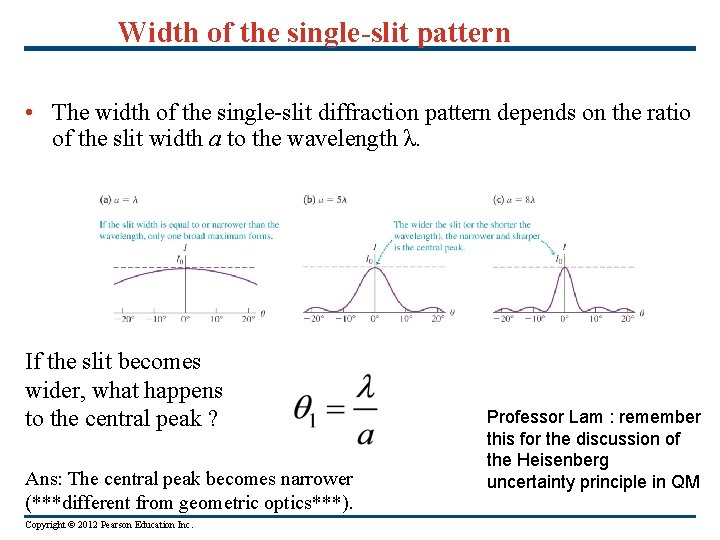
Width of the single-slit pattern • The width of the single-slit diffraction pattern depends on the ratio of the slit width a to the wavelength λ. If the slit becomes wider, what happens to the central peak ? Ans: The central peak becomes narrower (***different from geometric optics***). Copyright © 2012 Pearson Education Inc. Professor Lam : remember this for the discussion of the Heisenberg uncertainty principle in QM

Example of a single-slit pattern • Example (a) The intensity at the center of a single-slit diffraction pattern is I 0. What is the intensity at a point in the pattern where there is a 66 -radian phase difference between wavelets from the two edges of the slit? (b) If this point is 7 degrees from the central maximum, how many wavelengths across is the slit? • (a) • (b) Remember to work in radians not degrees Copyright © 2012 Pearson Education Inc.

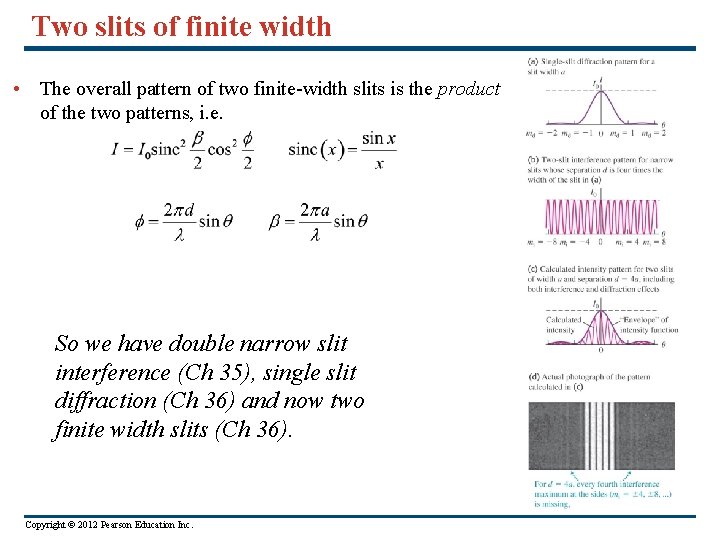
Two slits of finite width • The overall pattern of two finite-width slits is the product of the two patterns, i. e. So we have double narrow slit interference (Ch 35), single slit diffraction (Ch 36) and now two finite width slits (Ch 36). Copyright © 2012 Pearson Education Inc.

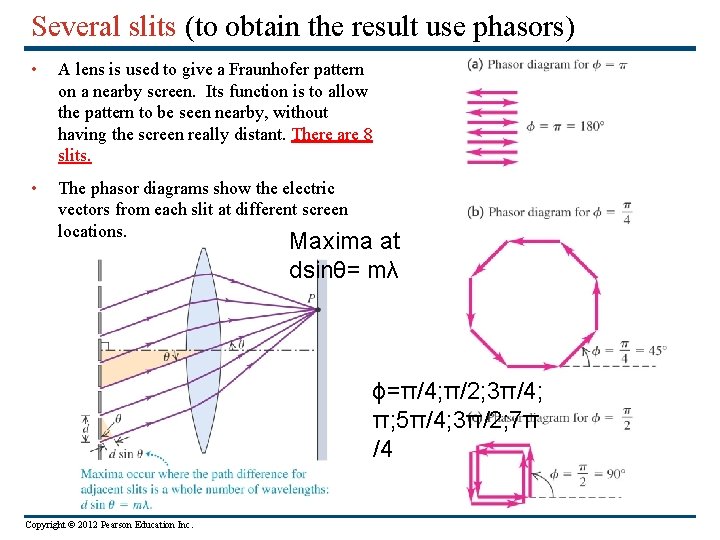
Several slits (to obtain the result use phasors) • A lens is used to give a Fraunhofer pattern on a nearby screen. Its function is to allow the pattern to be seen nearby, without having the screen really distant. There are 8 slits. • The phasor diagrams show the electric vectors from each slit at different screen locations. Maxima at dsinθ= mλ ϕ=π/4; π/2; 3π/4; π; 5π/4; 3π/2; 7π /4 Copyright © 2012 Pearson Education Inc.

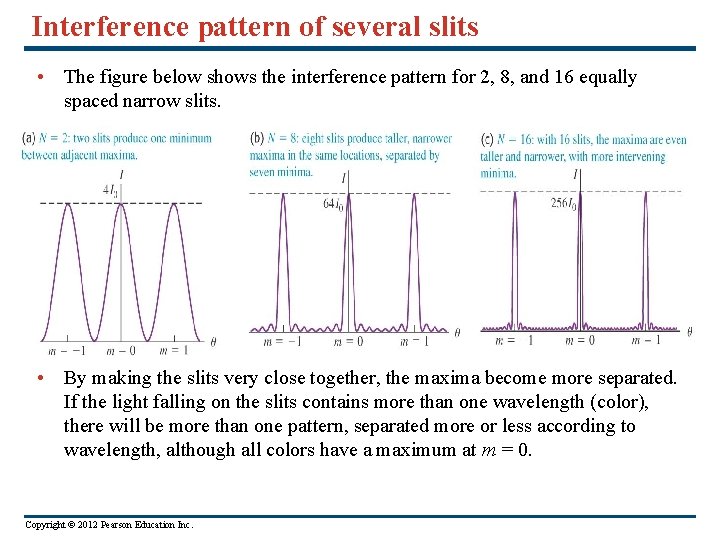
Interference pattern of several slits • The figure below shows the interference pattern for 2, 8, and 16 equally spaced narrow slits. • By making the slits very close together, the maxima become more separated. If the light falling on the slits contains more than one wavelength (color), there will be more than one pattern, separated more or less according to wavelength, although all colors have a maximum at m = 0. Copyright © 2012 Pearson Education Inc.

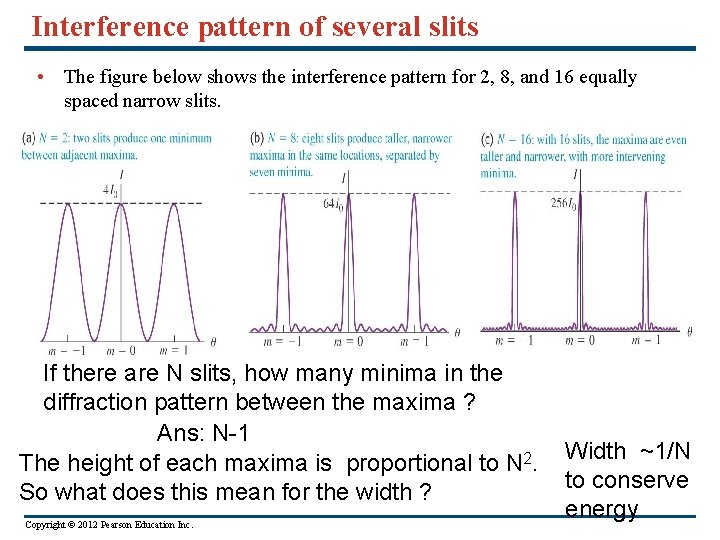
Interference pattern of several slits • The figure below shows the interference pattern for 2, 8, and 16 equally spaced narrow slits. If there are N slits, how many minima in the diffraction pattern between the maxima ? Ans: N-1 The height of each maxima is proportional to N 2. So what does this mean for the width ? Copyright © 2012 Pearson Education Inc. Width ~1/N to conserve energy