Examples of Control Systems Application Modeling the Ball

Examples of Control Systems Application

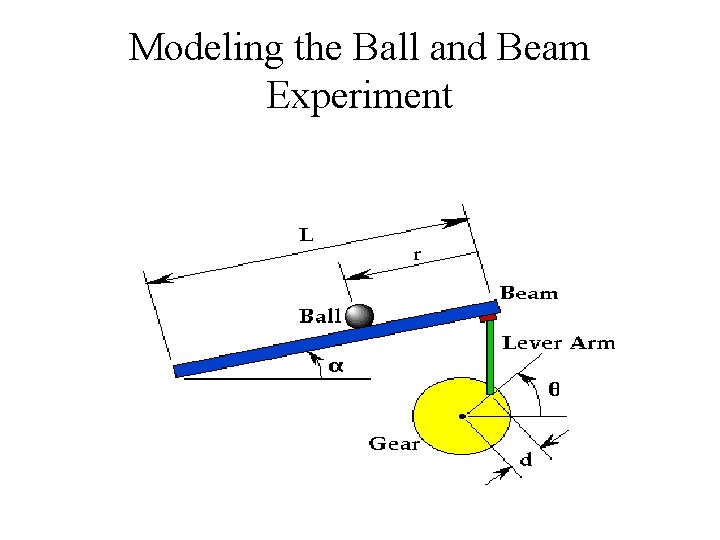
Modeling the Ball and Beam Experiment

Problem Setup M R d g L J r mass of the ball radius of the ball lever arm offset gravitational acceleration length of the beam ball's moment of inertia ball position coordinate 0. 11 kg 0. 015 m 0. 03 m 9. 8 m/s^2 1. 0 m 9. 99 e-6 kgm^2

The design criteria for this problem • Settling time less than 3 seconds • Overshoot less than 5%

System Equations Linearization of this equation about the beam angle, alpha = 0, gives us the following linear approximation of the system

System Equations The equation which relates the beam angle to the angle of the gear can be approximated as linear by the equation below Substituting this into the previous equation, we get

Transfer Function

State-Space

for our state-space example we will be using a slightly different model. The same equation for the ball still applies but instead of controlling the position through the gear angle, theta, we will control alpha-doubledot. This is essentially controlling the torque of the beam. Below is the representation of this system

State-Space

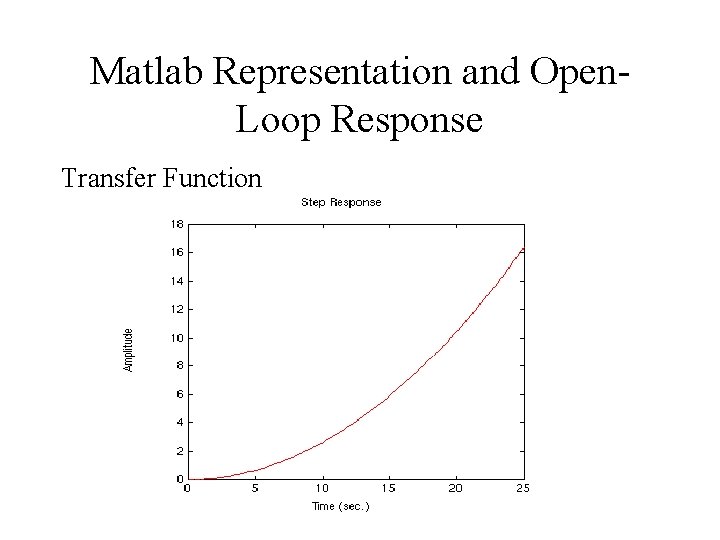
Matlab Representation and Open. Loop Response Transfer Function

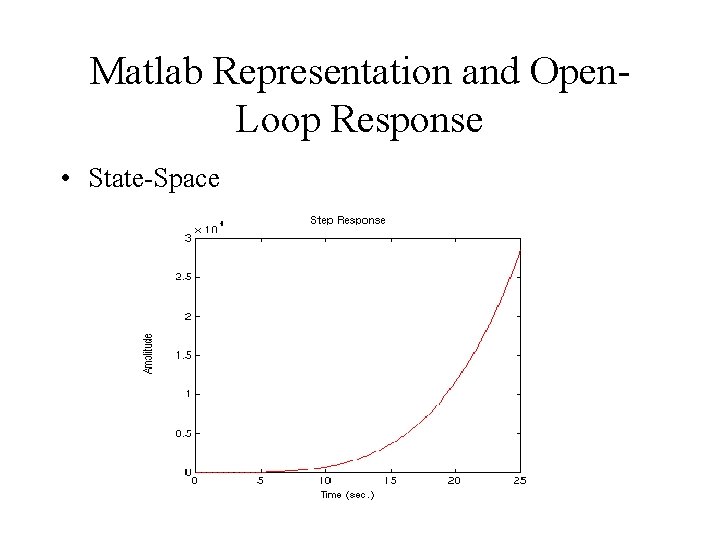
Matlab Representation and Open. Loop Response • State-Space

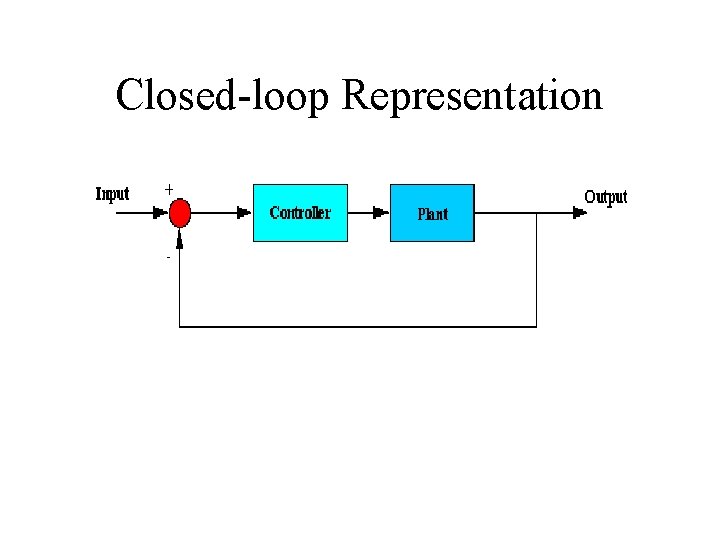
Closed-loop Representation

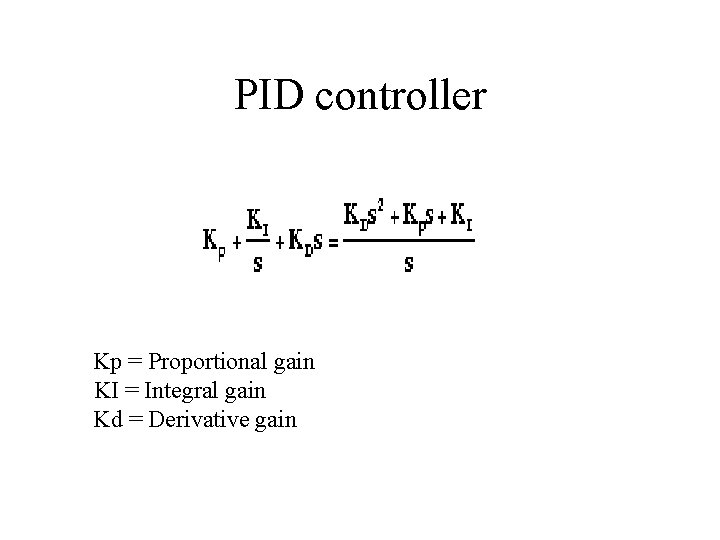
PID controller Kp = Proportional gain KI = Integral gain Kd = Derivative gain

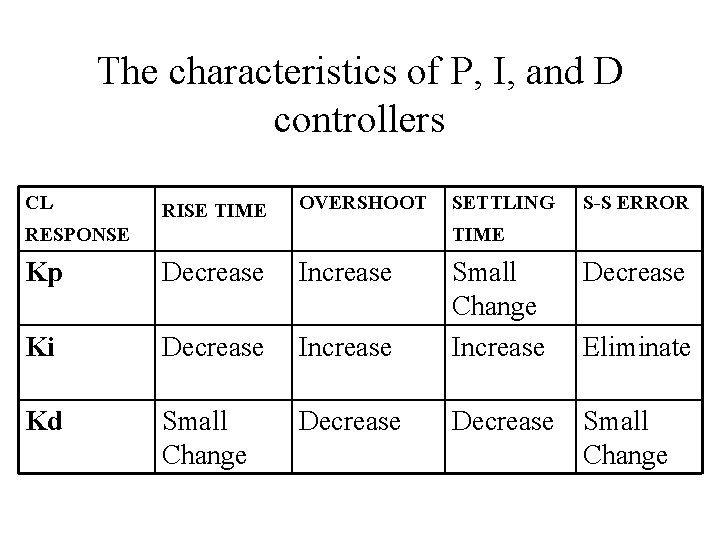
The characteristics of P, I, and D controllers CL RISE TIME OVERSHOOT RESPONSE SETTLING S-S ERROR TIME Kp Decrease Increase Small Change Increase Ki Decrease Kd Small Change Decrease Small Change Eliminate

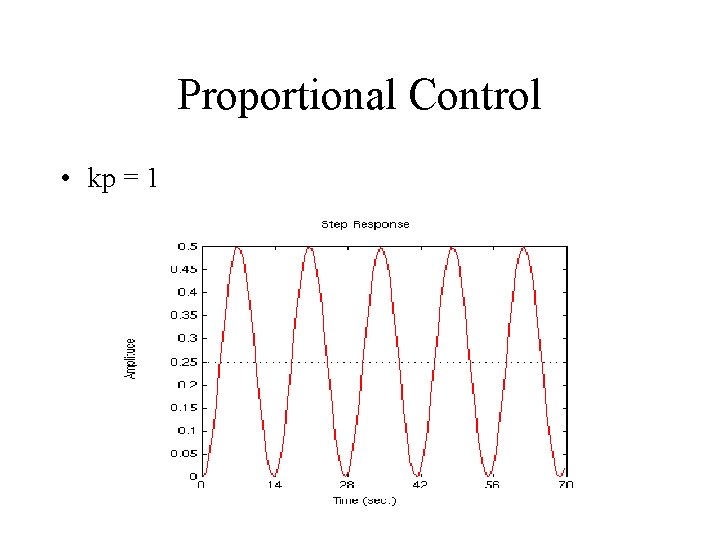
Proportional Control • kp = 1

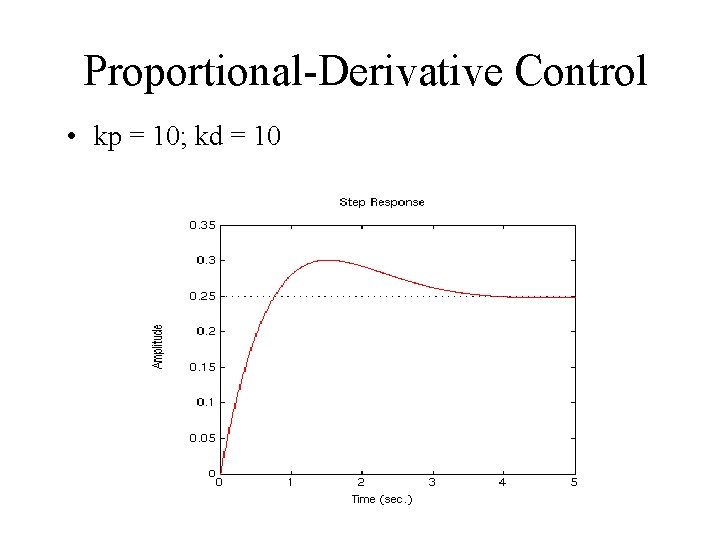
Proportional-Derivative Control • kp = 10; kd = 10

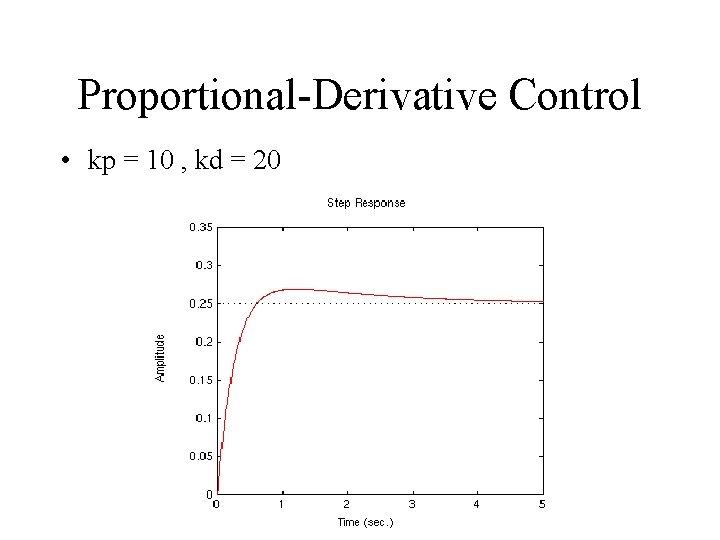
Proportional-Derivative Control • kp = 10 , kd = 20

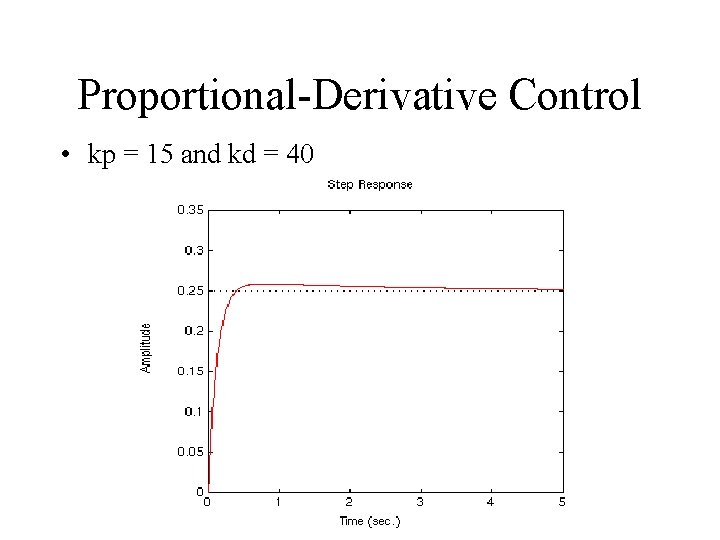
Proportional-Derivative Control • kp = 15 and kd = 40

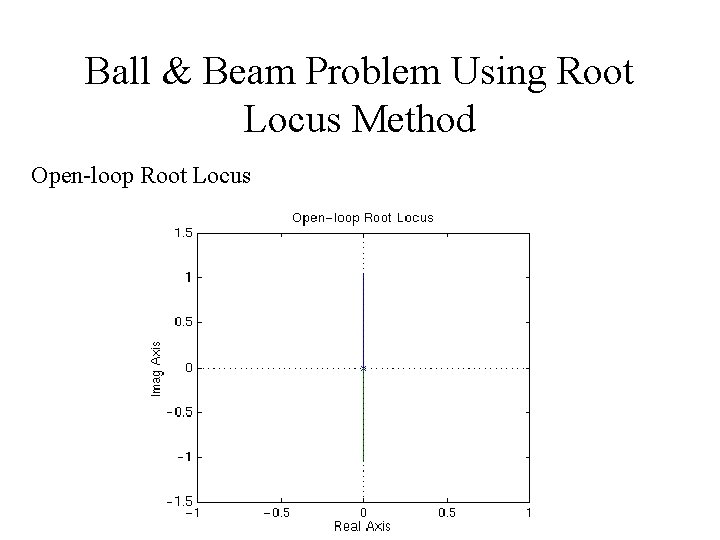
Ball & Beam Problem Using Root Locus Method Open-loop Root Locus

Ball & Beam Problem Using Root Locus Method From these equation damping ratio and natural frequency were found to be 0. 7 and 1. 9 respectively.

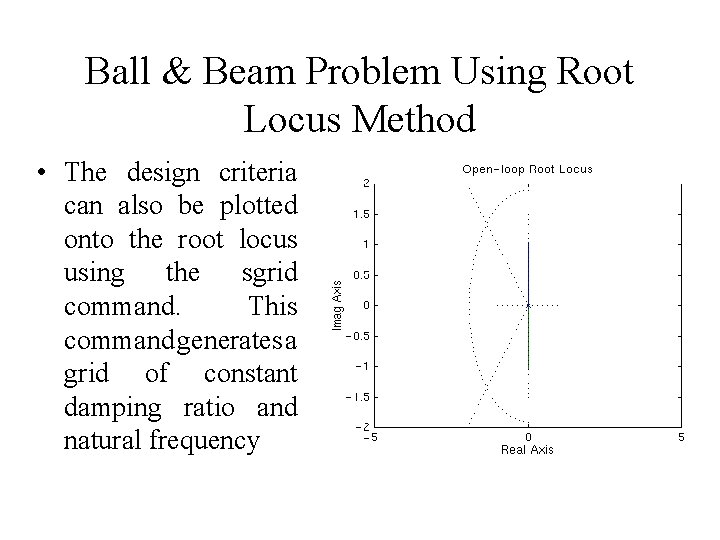
Ball & Beam Problem Using Root Locus Method • The design criteria can also be plotted onto the root locus using the sgrid command. This command generates a grid of constant damping ratio and natural frequency

Animation

Questions