Examples for Multiplying And Dividing Rational Expressions Monomials

Monomials (Multiply Across Method) The first method that can be used is to multiply

Monomials (Cross-Cancel Method) With cross-cancelling, you cancel out common factors in the numerator with

Monomials (Cross Cancel Method) 1 In this step both y 4 and y 3

Polynomials – Multiplying Across First, factor. X^2 -16 can be factored into (x+4)(x-4). 3

Polynomials – Cross Cancel The first step is to factor. The x^216 can factor

Slides: 6

Download presentation

Examples for Multiplying And Dividing Rational Expressions

Monomials (Multiply Across Method) The first method that can be used is to multiply across and then simplify. Now that you have them multiplied together, simplify The two 12’s cancel out, because 12/12 is one. The x 4 and x 6 leave a x 2 on the bottom. The y 3 and y 4 leave a y on the bottom of the equation. Therefore, the final answer is:

Monomials (Cross-Cancel Method) With cross-cancelling, you cancel out common factors in the numerator with the denominator. 2 1 In this first cross-cancel, both 4 and 2 can be divided by 2, therefore 4 becomes 2, and 2 becomes 1. 1 In this step, the 3 and the 6 can be divided since 3 goes into both 3 and 6 evenly. 3/3 is 1, and 3/6 is 2. 2 1 1 In this step, both of the 2 x 4 s cancel out, and 2 x 4/2 x 4 Is 1, therefore they both become 1 Note: do not copy the rational down each time you cross-cancel, it is easier to do this all at once, it is done this way solely for example purposes.

Monomials (Cross Cancel Method) 1 In this step both y 4 and y 3 can be divided by y 3. So, y 3/ y 3 is 1, and y 4 divided by y 3 is y. y Once you have simplified until you can’t simplify anymore, then just multiply across to get the answer. Notice, that this has the same final answer as using the other method.

Polynomials – Multiplying Across First, factor. X^2 -16 can be factored into (x+4)(x-4). 3 x+12 can also be factored. Take out the 3, making it 3(x+4). After factoring, multiply across. (x+4) is the numerator and 3(x+4)(x-4) is the denominator. Then, cancel. The two (x+4) from the numerator cancel out with the two (x+4) from the denominator. That is your final answer. The 1 takes the place of the (x+4) since there is nothing else on the top. You do not have to multiply back

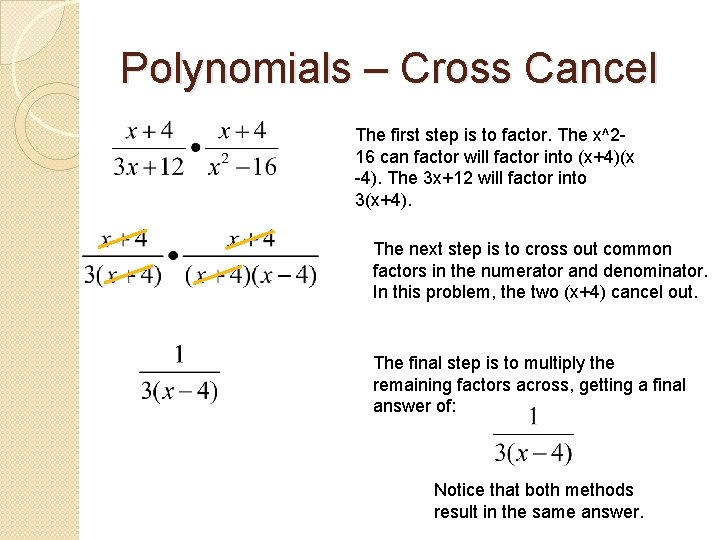
Polynomials – Cross Cancel The first step is to factor. The x^216 can factor will factor into (x+4)(x -4). The 3 x+12 will factor into 3(x+4). The next step is to cross out common factors in the numerator and denominator. In this problem, the two (x+4) cancel out. The final step is to multiply the remaining factors across, getting a final answer of: Notice that both methods result in the same answer.