Example of Weighted Voting System Undersea target detection

Example of Weighted Voting System Undersea target detection system

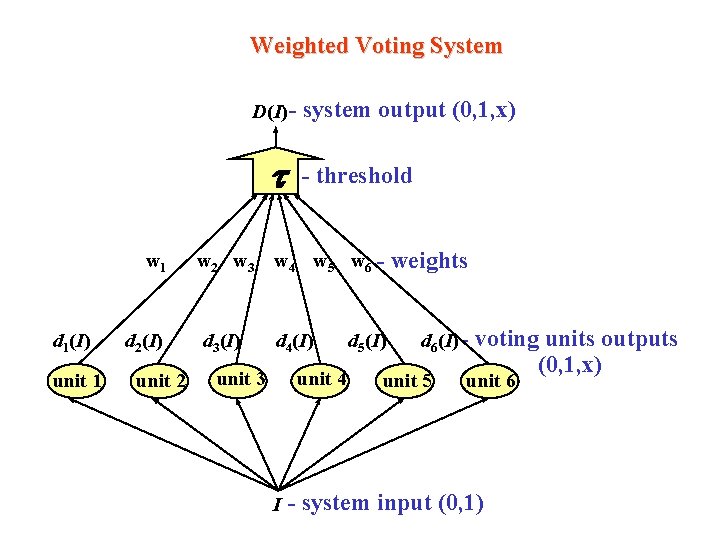
Weighted Voting System D(I) - t w 1 d 1(I) unit 1 d 2(I) unit 2 w 3 d 3(I) system output (0, 1, x) - threshold w 4 w 5 w 6 - d 4(I) unit 3 unit 4 I d 5(I) weights d 6(I) - unit 5 voting units outputs (0, 1, x) unit 6 - system input (0, 1)

Decision Making Rule Total weight of units voting for the proposition acceptance Total weight of units voting for the proposition rejection System output

Decision Making Rule (1 -t)Wn 1 t. Wn 0 Accept Reject if (1 -t)Wn 1 -t. Wn 0<0 if Wn 1=Wn 0=0 otherwise

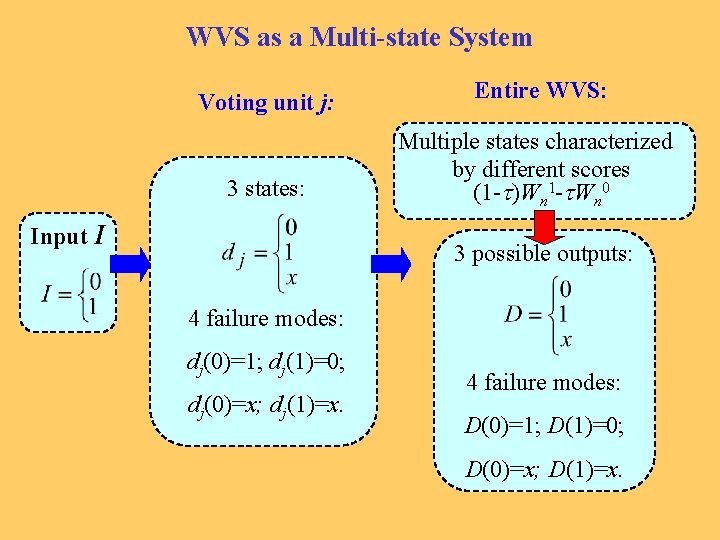
WVS as a Multi-state System Voting unit j: Entire WVS: 3 states: Multiple states characterized by different scores (1 -t)Wn 1 -t. Wn 0 Input I 3 possible outputs: 4 failure modes: dj(0)=1; dj(1)=0; dj(0)=x; dj(1)=x. 4 failure modes: D(0)=1; D(1)=0; D(0)=x; D(1)=x.

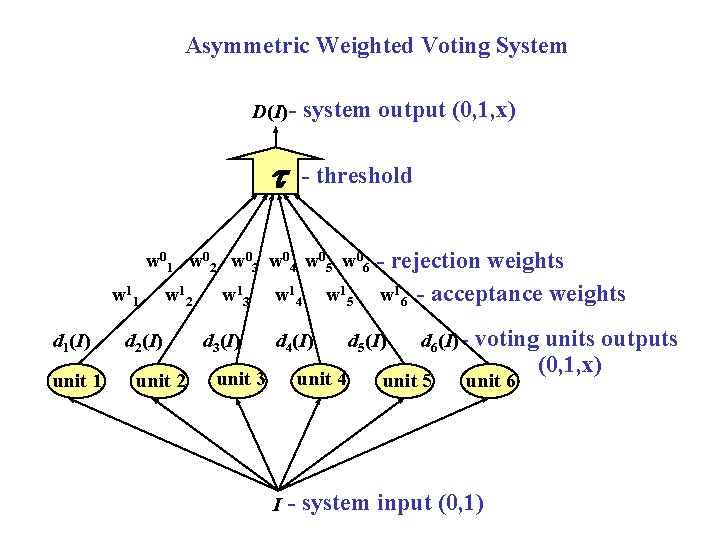
Asymmetric Weighted Voting System D(I) - t system output (0, 1, x) - threshold w 0 1 w 0 2 w 0 3 w 0 4 w 0 5 w 0 6 w 1 1 d 1(I) unit 1 w 1 2 d 2(I) unit 2 w 1 3 d 3(I) w 1 4 w 1 5 d 4(I) unit 3 unit 4 I - rejection weights w 16 - acceptance weights d 5(I) d 6(I) - unit 5 voting units outputs (0, 1, x) unit 6 - system input (0, 1)

Decision Making Rule Total weight of units voting for the proposition acceptance Total weight of units voting for the proposition rejection System output

System Parameters Types of Errors dj(0)=1 (unit fails stuck-at-1) too optimistic q 01(j) dj(1)=0 (unit fails stuck-at-0) too pessimistic q 10(j) dj(I)=x (unit fails stuck-at-x) too indecisive q 1 x(j), q 0 x(j) Voting unit parameters Decision making time tj Rejection weight w j 0 Acceptance weight w j 1 System threshold t adjustable

Universal generating function technique Score distribution for a single voter Composition operator Score distribution for m voters

Optimization problems System Success Probability Optimal adjustment problem (w 01, w 11, …, w 0 n, w 1 n , t) = arg{R(w 01, w 11, …, w 0 n, w 1 n , t) max}

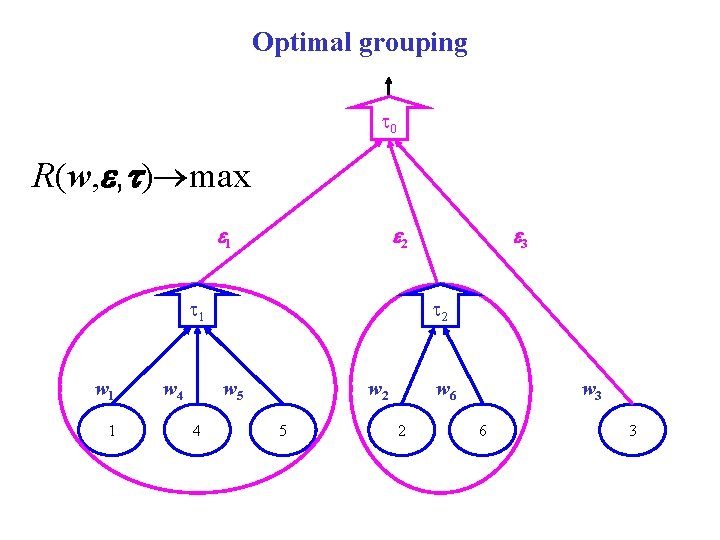
Optimal grouping t 0 R(w, e, t) max e 1 e 2 t 1 w 1 1 w 4 t 2 w 5 4 e 3 w 2 5 w 6 2 w 3 6 3

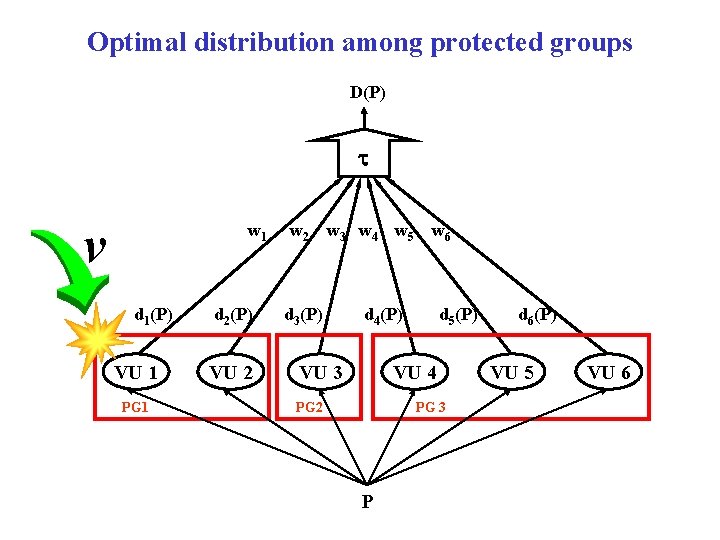
Optimal distribution among protected groups D(P) t v w 1 d 1(P) VU 1 PG 1 d 2(P) VU 2 w 3 w 4 w 5 d 3(P) w 6 d 4(P) VU 3 d 5(P) VU 4 PG 2 PG 3 P d 6(P) VU 5 VU 6

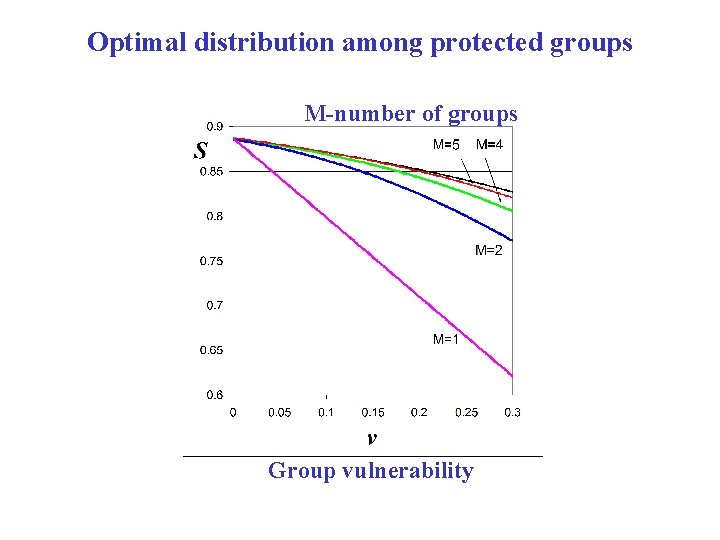
Optimal distribution among protected groups M-number of groups Group vulnerability

Order of voting decisions tn t 1 t 2 … tm … Total weight of units with tj tm voting for the proposition acceptance Total weight of units with tj tm voting for the proposition rejection

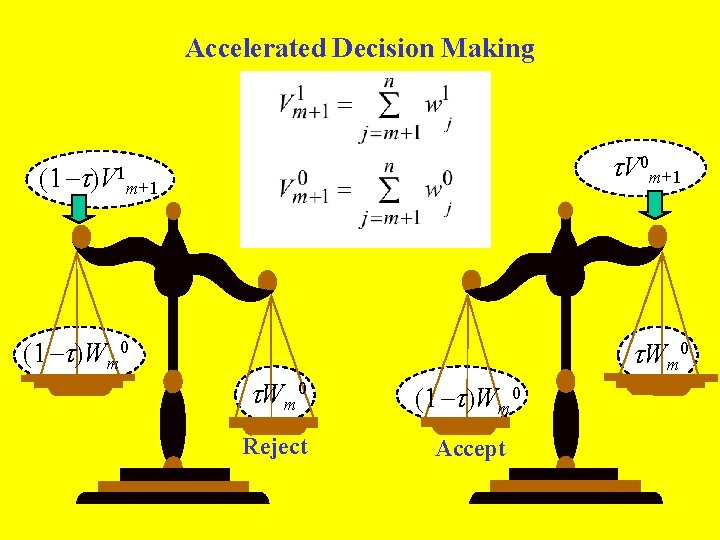
Accelerated Decision Making (1 -t t. V 0 m+1 )V 1 m+1 (1 -t)Wm 0 t Wm 0 (1 -t)Wm 0 Reject Accept

System reliability and expected decision time Qijm probability of making the decision D(i)=j at the time tm p 0, p 1 - input distribution

Voting system optimization problem ax m R Two-objective problem: T min T Constrained problem: R max | T<T* R (w 01, w 11, …, w 0 n, w 1 n , t) = arg{R(w 01, w 11, …, w 0 n, w 1 n , t) max} subject to T(w 01, w 11, …, w 0 n, w 1 n , t) T*

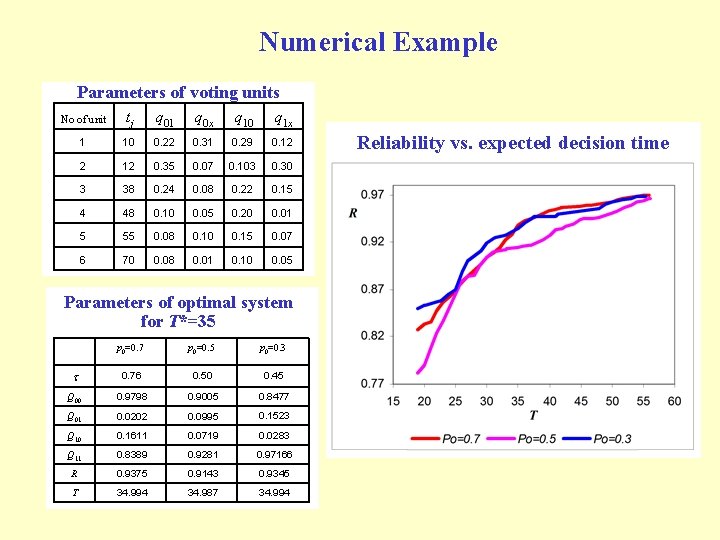
Numerical Example Parameters of voting units No of unit tj q 01 q 0 x q 10 q 1 x 1 10 0. 22 0. 31 0. 29 0. 12 2 12 0. 35 0. 07 0. 103 0. 30 3 38 0. 24 0. 08 0. 22 0. 15 4 48 0. 10 0. 05 0. 20 0. 01 5 55 0. 08 0. 10 0. 15 0. 07 6 70 0. 08 0. 01 0. 10 0. 05 Parameters of optimal system for T*=35 p 0=0. 7 p 0=0. 5 p 0=0. 3 t 0. 76 0. 50 0. 45 Q 00 0. 9798 0. 9005 0. 8477 Q 01 0. 0202 0. 0995 0. 1523 Q 10 0. 1611 0. 0719 0. 0283 Q 11 0. 8389 0. 9281 0. 97166 R 0. 9375 0. 9143 0. 9345 T 34. 994 34. 987 34. 994 Reliability vs. expected decision time

References 1. Weighted voting systems: reliability versus rapidity, G. Levitin, Reliability Engineering & System Safety, 89(2) pp. 177 -184 (2005). 2. Maximizing survivability of vulnerable weighted voting systems, G. Levitin, Reliability Engineering & System Safety, vol. 83, pp. 17 -26, (2003). 3. Threshold optimization for weighted voting classifiers, G. Levitin, Naval Research Logistics, vol. 50 (4), pp. 322 -344, (2003). 4. Asymmetric weighted voting systems, G. Levitin, Reliability Engineering & System Safety, vol. 76, pp. 199 -206, (2002). 5. Evaluating correct classification probability for weighted voting classifiers with plurality voting, G. Levitin, European Journal of Operational Research, vol. 141, pp. 596 -607, (2002). 6. Analysis and optimization of weighted voting systems consisting of voting units with limited availability, G. Levitin, Reliability Engineering & System Safety, vol. 73, pp. 91100, (2001). 7. Optimal unit grouping in weighted voting systems, G. Levitin, Reliability Engineering & System Safety vol. 72, pp. 179 -191, (2001). 8. Reliability optimization for weighted voting system, G. Levitin, A. Lisnianski, Reliability Engineering & System Safety, vol. 71, pp. 131 -138, (2001).