Example of formula defun roots a b c

Example of formula (defun roots (a b c) (list (/ (+ (- b) (sqrt (- (expt b 2) (* 4 a c)) )) (* 2 a)) )) Returns a list of solutions to a quadratic equation

eval and quote > (eval (cdr '(a + 2 3))) 5 > (setq a 'b) b > a b > b error: unbound variable - b if continued: try evaluating symbol again 1> [ back to top level ] > (set 'a 'b) Value of atom a b is atom b > (eval ''a)) b For every quote > 'a there is an eval a

eval and quote > (eval '(quote a))) b > 'a a > (eval '(list '* 9 6)) (* 9 6) > (eval '(list * 9 6))) error: bad function - (* 9 6) 1> [ back to top level ] > (eval '(list '* 9 6))) 54 For every quote there is an eval

Examples of tail recursion • If last operation in function is recursive call, overwrite actuals and go to beginning of code: (defun last (lis) ; finds the last element of the list (if (null? (cdr lis) (car lis)) (last (crd lis)))) ; can be done with loop (defun length (lis) ; calculates the length of the list (if (null? lis) 0) (+ 1 (length (cdr lis)))) ; not tail recursive!

Example of Tree Recursion: Fibonacci • Writing a function to compute the nth Fibonacci number – Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, … • fib(0) = 0 • fib(1) = 1 • fib(n) = fib(n-2) + fib(n-1)

Short Version of tree recursion (defun fib (n) (cond ((eql n 0) ((eql n 1) (t (+ (fib 0) ; base case 1) ; base case (- n 1)) ; recursively compute fib(n) (- n 2))))))

Complete Version with Error Checking and Comments (defun fib (n) "Computes the nth Fibonacci number. " (cond ((or (not (integerp n)) (< n 0)) ; error case (error "~s must be an integer >= 0. ~&" n)) ((eql n 0) 0) ; base case ((eql n 1) 1) ; base case (t (+ (fib (- n 1)) ; recursively compute fib(n) (fib (- n 2))))))

Problems: 1. Write a function (power 3 2) = 3^2 = 9 2. Write a function that counts the number of atoms in an expression. (count-atoms '(a (b) c)) --> 3 3. (count-anywhere 'a '(a ((a) b) a)) --> 3 4. (dot-product '(10 20) '(3 4)) --> 10 x 3 + 20 x 4 = 110 5. Write a function (flatten '(a (b) () ((c)))) --> (a b c) which removes all levels of parenthesis and returns a flat list of atoms. 6. Write a function (remove-dups '(a 1 1 a b 2 b)) --> (a 1 b 2) which removes all duplicate atoms from a flat list. (Note: there is a built-in remove-duplicates in Common Lisp, do not use it).

Solutions 1 -3 (defun power (a b) "compute a^b - (power 3 2) ==> 9" (if (= b 0) 1 (* a (power a (- b 1))))) (defun count-atoms (exp) "count atoms in expresion - (count-atoms '(a (b) c)) ==> 3" (cond ((null exp) 0) ((atom exp) 1) (t (+ (count-atoms (first exp)) (count-atoms (rest exp)))))) (defun count-anywhere (a exp) "count performances of a in expresion (count-anywhere 'a '(a ((a) b) (a))) ==> 3" (cond ((null exp) 0) ((atom exp) (if (eq a exp) 1 0)) (t (+ (count-anywhere a (first exp)) (count-anywhere a (rest exp))))))

Solutions (defun flatten (exp) "removes all levels of paranthesis and returns flat list of atomsi (flatten '(a (b) () ((c)))) ==> (a b c)" (cond ((null exp) nil) ((atom exp) (list exp)) (t (append (flatten (first exp)) (flatten (rest exp))))))

Iteration – adding all elements from a list • Iteration is done by recursion • Analogous to while-loop (defun plus-red (a) (if (null a) 0 (plus (car a) (plus-red (cdr a)) )) )

Nested Loops • Example : Cartesian product (defun all-pairs (M N) (if (null M) nil (append (distl (car M) N) (all-pairs (cdr M ) N )) )) (defun distl (x N) (if (null N) nil (cons (list x (car N)) (distl x (cdr N)) )) )

Functional arguments and abstraction Suppress details of loop control and recursion example: applying a function to all elements of list (defun mapcar (f x) Another definition of mapcar uses if not cond (if (null x) nil (cons (f (car x)) (mapcar f (cdr x)) )) )

Hierarchical structures • Are difficult to handle iteratively example: equal function • eq only handles atoms • initial states – If x and y are both atoms (equal x y) = (eq x y) – If exactly one of x and y is atom (equal x y) = nil (and (atom x) (atom y) (eq x y)) • use car and cdr to write equal recursively

Equivalency of recursion and iteration • it may be seemed that recursion is more powerful than iteration • in theory these are equivalent • As we said iteration can be done by recursion • by maintaining a stack of activation records we can convert a recursive program to an iterative one.

Genetic algorithm Common Lisp code

REDUCE (with 3 arguments) a function to be applied to every element of list x Final value returned a list (defun reduce (f a x) (if (null x) a (f (car x) (reduce f a (cdr x) )) ) ) (reduce #'* '(1 2 3 4 5)) => 120 (* 1 (* 2 (* 3 (* 4 5)))) => 120 Here only two values

Few more examples of using function reduce Examples: (reduce #'* '(1 2 3 4 5)) => 120 (reduce #'append '((1) (2)) : initial-value '(i n i t) ) => (I N I T 1 2) ; ; list (I N I T) with appended (1) with appended (2) (reduce #'append '((1) (2)) : from-end t : initial-value '(i n i t)) => (1 2 I N I T) (reduce #'- '(1 2 3 4)) == (- (- (- 1 2) 3) 4) => -8 (reduce #'- '(1 2 3 4) : from-end t) ; Alternating sum. == (- 1 (- 2 (- 3 4))) => -2 (reduce #'+ '()) => 0 (reduce #'+ '(3)) => 3 (reduce #'+ '(foo)) => FOO

Few more examples of using function reduce (reduce #'+ '(foo)) => FOO (reduce #'list '(1 2 3 4)) => (((1 2) 3) 4) ; ; assumes to start from beginning of argument list (list 1 2) 3) 4) (reduce #'list '(1 2 3 4) : from-end t) => (1 (2 (3 4))) (reduce #'list '(1 2 3 4) : initial-value 'foo) => ((((foo 1) 2) 3) 4) (reduce #'list '(1 2 3 4) : from-end t : initial-value 'foo) => (1 (2 (3 (4 foo))))

Few more functions reduce uses a binary operation, function, to combine the elements of sequence bounded by start and end. The function must accept as arguments two elements of sequence or the results from combining those elements. The function must also be able to accept no arguments. If key is supplied, it is used to extract the values to reduce. The key function is applied exactly once to each element of sequence in the order implied by the reduction order but not to the value of initial -value, if supplied. The key function typically returns part of the element of sequence. If key is not supplied or is nil, the sequence element itself is used. The reduction is left-associative, unless from-end is true in which case it is right-associative. If initial-value is supplied, it is logically placed before the subsequence (or after it if from-end is true) and included in the reduction operation. In the normal case, the result of reduce is the combined result of function's being applied to successive pairs of elements of sequence. If the subsequence contains exactly one element and no initial-value is given, then that element is returned and function is not called. If the subsequence is empty and an initialvalue is given, then the initial-value is returned and function is not called. If the subsequence is empty and no initial-value is given, then the function is called with zero arguments, and reduce returns whatever function does. This is the only case where the function is called with other than two arguments.

Few more examples of function some • SOME function searches the sequences for values for which predicate returns true. • It there is such list of values that occupy same index in each sequence, return value is true, otherwise false. (some #'alphanumericp "") => NIL (some #'alphanumericp ". . . ") => NIL (some #'alphanumericp "ab. . . ") => T (some #'alphanumericp "abc") => T (some #'< '(1 2 3 4) '(2 3 4 5)) => T (some #'< '(1 2 3 4)) => NIL

Reminder of function let* • let* is similar to let, but the bindings of variables are performed sequentially rather than in parallel. • • The expression for the init-form of a var can refer to vars previously bound in the let*. The form (let* ((var 1 init-form-1) (var 2 init-form-2). . . (varm init-form-m)) declaration 1 declaration 2. . . declarationp form 1 form 2. . . formn) • first evaluates the expression init-form-1, • • then binds the variable var 1 to that value; then it evaluates init-form-2 and binds var 2, and so on. • The expressions formj are then evaluated in order; the values of all but the last are discarded (that is, the body of let* is an implicit progn).

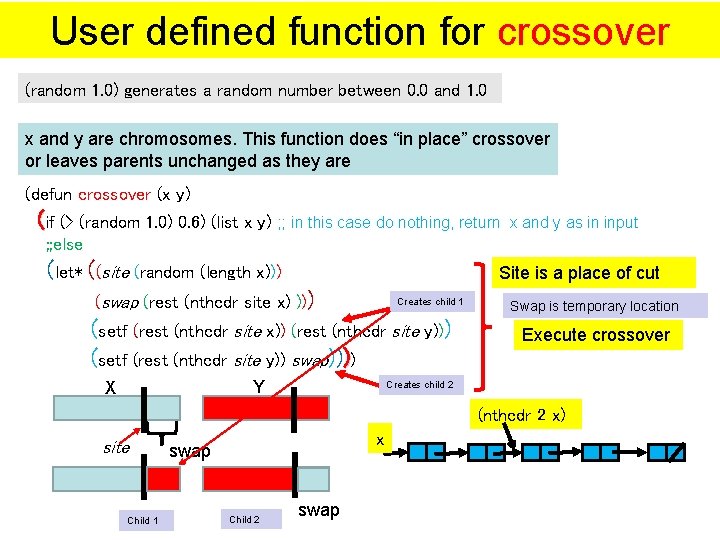
User defined function for crossover (random 1. 0) generates a random number between 0. 0 and 1. 0 x and y are chromosomes. This function does “in place” crossover or leaves parents unchanged as they are (defun crossover (x y) (if (> (random 1. 0) 0. 6) (list x y) ; ; in this case do nothing, return x and y as in input ; ; else (let* ((site (random (length x))) Site is a place of cut (swap (rest (nthcdr site x) ))) Creates child 1 (setf (rest (nthcdr site x)) (rest (nthcdr site y))) (setf (rest (nthcdr site y)) swap)))) Y X Swap is temporary location Execute crossover Creates child 2 (nthcdr 2 x) site Child 1 x swap Child 2 swap

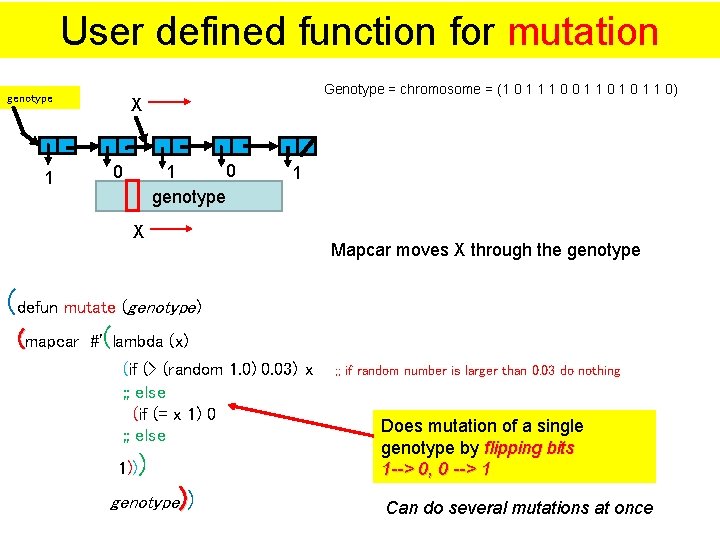
User defined function for mutation genotype 1 Genotype = chromosome = (1 0 1 1 1 0 0 1 1 0) X 0 1 genotype 0 1 X (defun mutate (genotype) Mapcar moves X through the genotype (mapcar #'(lambda (x) (if (> (random 1. 0) 0. 03) x ; ; else (if (= x 1) 0 ; ; else 1))) genotype)) ; ; if random number is larger than 0. 03 do nothing Does mutation of a single genotype by flipping bits 1 --> 0, 0 --> 1 Can do several mutations at once

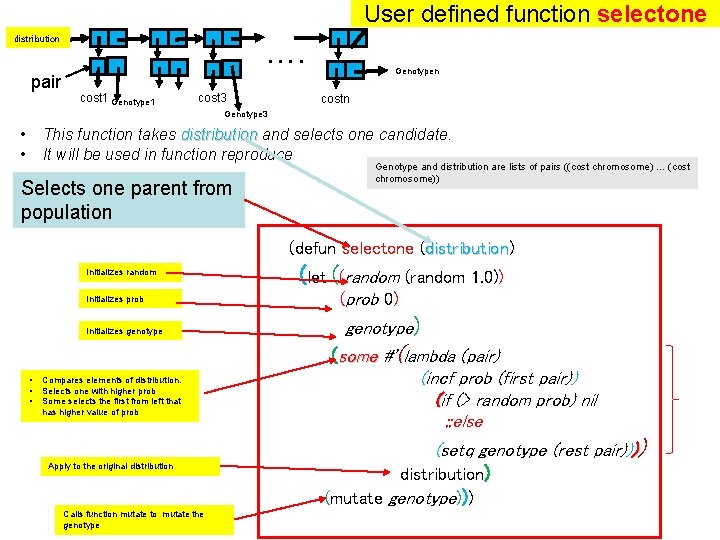
User defined function selectone distribution pair …. 1 cost 1 Genotype 1 cost 3 Genotypen costn Genotype 3 • • This function takes distribution and selects one candidate. distribution It will be used in function reproduce Selects one parent from population Genotype and distribution are lists of pairs ((cost chromosome) … (cost chromosome)) (defun selectone (distribution) distribution Initializes random Initializes prob Initializes genotype • • • Compares elements of distribution. Selects one with higher prob Some selects the first from left that has higher value of prob Apply to the original distribution Calls function mutate to mutate the genotype (let ((random 1. 0)) (prob 0) genotype) (some #'(lambda (pair) (incf prob (first pair)) (if (> random prob) nil ; ; else (setq genotype (rest pair)))) distribution) (mutate genotype)))

Function fitness calculates fitness of a chromosome x (genotype, object, candidate) x Calculate fitness function Function list 2 num converts list of binary bits s to a number Calculates fitness of a genotype x (defun fitness (x) (let ((xarg (/ (list 2 num x) 1073741823. 0)) (v '(0. 5 0. 25 1. 0 0. 25)) (c '(0. 125 0. 375 0. 625 0. 875)) Set parameters (w 0. 003)) (reduce #'+ (mapcar #'(lambda (vi ci) (let ((xc (- xarg ci))) (* vi (exp (* -1 (/ (* 2 w)) xc xc))))) v c)))) Chromosome is now a single number xarg • -2 w • Fitness = ( vi * i=1 e (xarg-ci) 2 ( i=4 This is of course just one particular example of particular example calculating the cost fitness function. You create your own fitness function for your problem. REMINDER (reduce #'* '(1 2 3 4 5)) => 120

User defined function distribution Distributes initial population Takes the initial population and distributes it according to fitness function (defun distribution (population) (let* ((genotypes (remove-duplicates population : test #'equal)) (sum (apply #'+ (mapcar #'fitness genotypes)))) Creates sum of fitness values Creates genotypes by removing the duplicates from population Uses function fitness Calculates fitness of all elements from list genotypes (mapcar #'(lambda (x) (cons (/ (fitness x) sum) x)) genotypes))) Creates a pair of normalized fitness and a genotype x Creates list of pairs for all elements of list genotypes

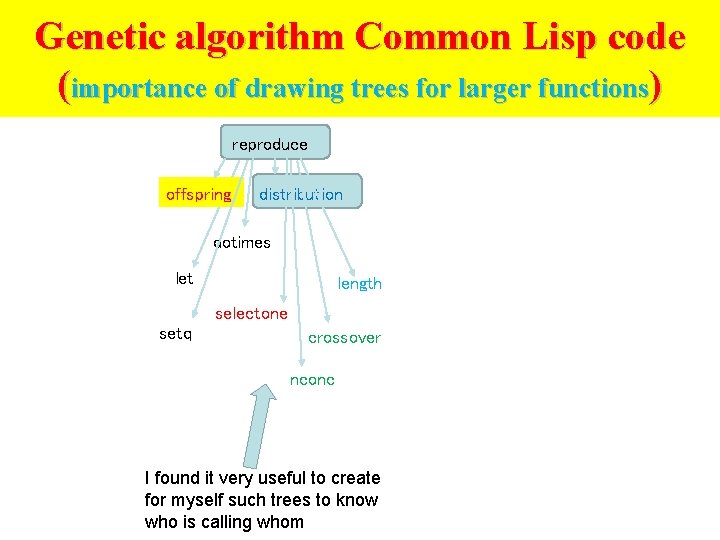
Genetic algorithm Common Lisp code (importance of drawing trees for larger functions) reproduce offspring distribution dotimes let length selectone setq crossover nconc I found it very useful to create for myself such trees to know who is calling whom

Genetic algorithm Common Lisp code: Takes population as argument. This can be some list of random binary lists of the same length each. (defun reproduce (population) (let ( (offspring nil) (d (distribution population) )) Initializes offspring to empty list Distributed population (dotimes (i (/ (length population) 2) ) (let ( (x (selectone d) ) (y (selectone d)) ) (crossover x y) Distributes initial population Repeats for the length of half population Selects parent x, one from population Selects parent y, one from population Does crossover of parents x and y (setq offspring (nconc (list x y) offspring) ) )) offspring)) Returns new list offspring End of adding new children to list offspring Creates new list offspring by adding new children x and y to old list offspring

Building Problem Solvers in LISP • http: //www. qrg. northwestern. edu/bps/directory. html

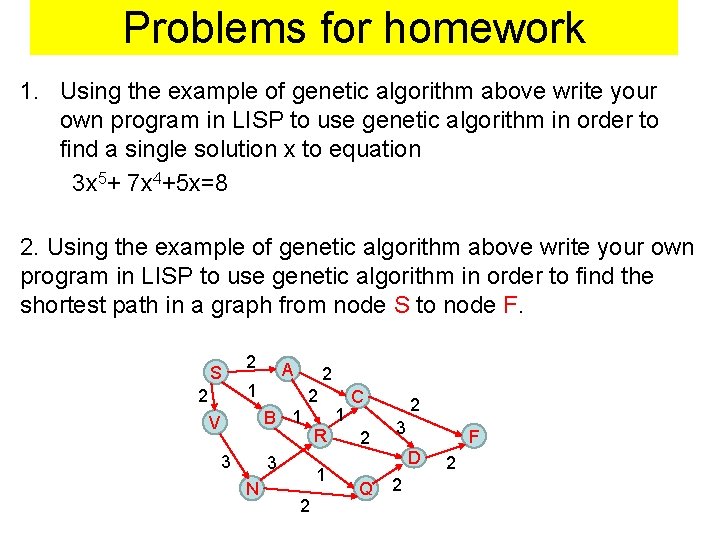
Problems for homework 1. Using the example of genetic algorithm above write your own program in LISP to use genetic algorithm in order to find a single solution x to equation 3 x 5+ 7 x 4+5 x=8 2. Using the example of genetic algorithm above write your own program in LISP to use genetic algorithm in order to find the shortest path in a graph from node S to node F. S 2 2 A 2 1 2 B 1 V 3 3 N R 1 2 1 C 2 2 3 F D Q 2 2