Example Intersection of a Prism with a Plane

Example: Intersection of a Prism with a Plane - Development Additional Task to the multimedia book „Darstellende Geometrie/ 3 D-Geometry“, published by Veritas Educational Edition Student Edition ISBN - 978 -3 -7058 -9079 -4 ISBN - 978 -3 -7058 -9293 -4 Special edition for teachers: The print version shows handouts of theory and worked-out examples. Each handout can be printed in colour and is also suitable as a solutions handout. Through the use of animated Power. Point files it is possible to structure the lessons in a contemporary and innovative manner for students. Special edition for students: The print version consists of well prepared worksheets to start working right away. On the CD you will find colourful Power. Point presentations, including theory as well as solved examples with step-by-step explanations. This provides a highly efficient technique in developing an understanding of geometry and its concepts. for more DETAILS and ORDER 1

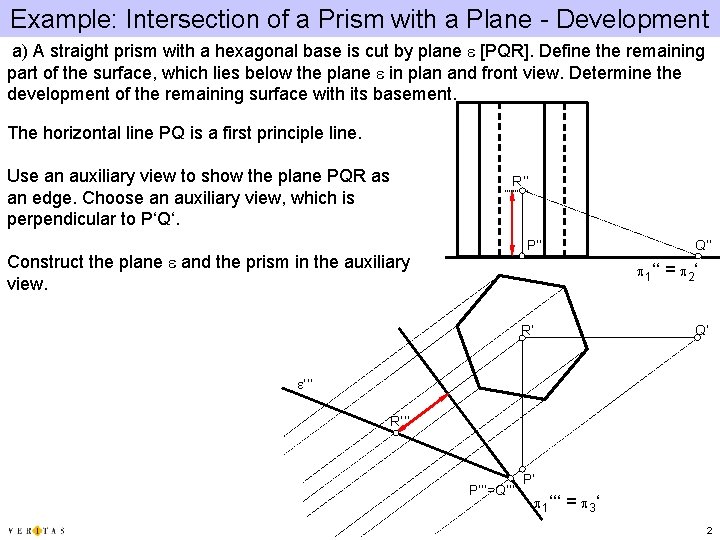
Example: Intersection of a Prism with a Plane - Development a) A straight prism with a hexagonal base is cut by plane e [PQR]. Define the remaining part of the surface, which lies below the plane e in plan and front view. Determine the development of the remaining surface with its basement. The horizontal line PQ is a first principle line. Use an auxiliary view to show the plane PQR as an edge. Choose an auxiliary view, which is perpendicular to P‘Q‘. R‘‘ P‘‘ Construct the plane e and the prism in the auxiliary view. Q‘‘ p 1‘‘ R‘ = p 2 ‘ Q‘ e‘‘‘ R‘‘‘ P‘‘‘=Q‘‘‘ P‘ p 1‘‘‘ = p 3 ‘ 2

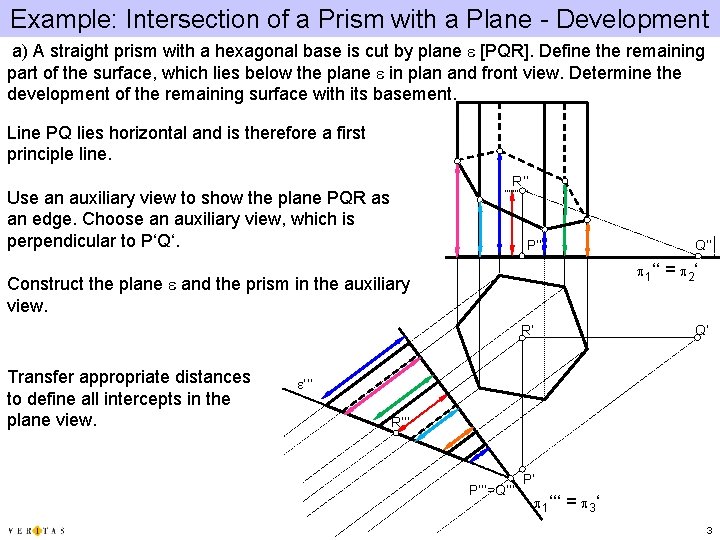
Example: Intersection of a Prism with a Plane - Development a) A straight prism with a hexagonal base is cut by plane e [PQR]. Define the remaining part of the surface, which lies below the plane e in plan and front view. Determine the development of the remaining surface with its basement. Line PQ lies horizontal and is therefore a first principle line. R‘‘ Use an auxiliary view to show the plane PQR as an edge. Choose an auxiliary view, which is perpendicular to P‘Q‘. P‘‘ Q‘‘ p 1‘‘ Construct the plane e and the prism in the auxiliary view. R‘ Transfer appropriate distances to define all intercepts in the plane view. = p 2 ‘ Q‘ e‘‘‘ R‘‘‘ P‘‘‘=Q‘‘‘ P‘ p 1‘‘‘ = p 3 ‘ 3

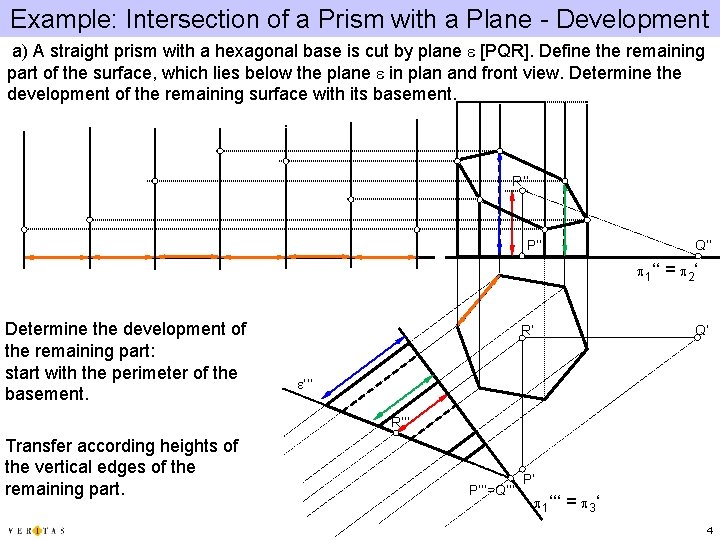
Example: Intersection of a Prism with a Plane - Development a) A straight prism with a hexagonal base is cut by plane e [PQR]. Define the remaining part of the surface, which lies below the plane e in plan and front view. Determine the development of the remaining surface with its basement. R‘‘ P‘‘ Q‘‘ p 1‘‘ Determine the development of the remaining part: start with the perimeter of the basement. R‘ = p 2 ‘ Q‘ e‘‘‘ R‘‘‘ Transfer according heights of the vertical edges of the remaining part. P‘‘‘=Q‘‘‘ P‘ p 1‘‘‘ = p 3 ‘ 4

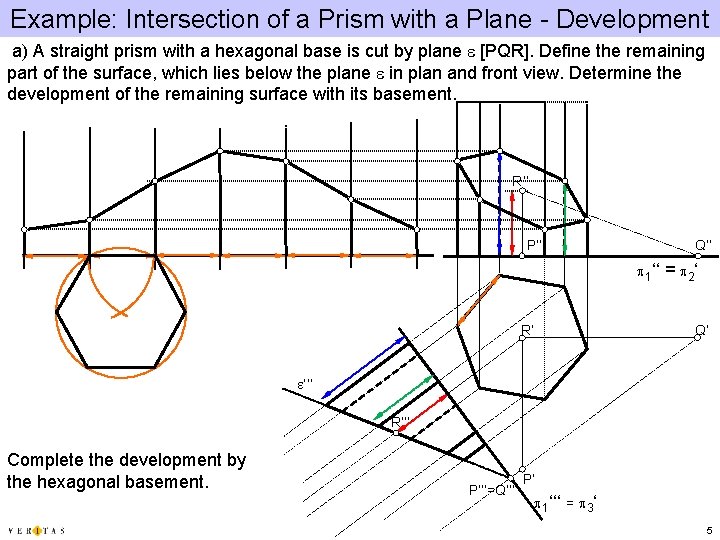
Example: Intersection of a Prism with a Plane - Development a) A straight prism with a hexagonal base is cut by plane e [PQR]. Define the remaining part of the surface, which lies below the plane e in plan and front view. Determine the development of the remaining surface with its basement. R‘‘ P‘‘ Q‘‘ p 1‘‘ R‘ = p 2 ‘ Q‘ e‘‘‘ R‘‘‘ Complete the development by the hexagonal basement. P‘‘‘=Q‘‘‘ P‘ p 1‘‘‘ = p 3‘ 5

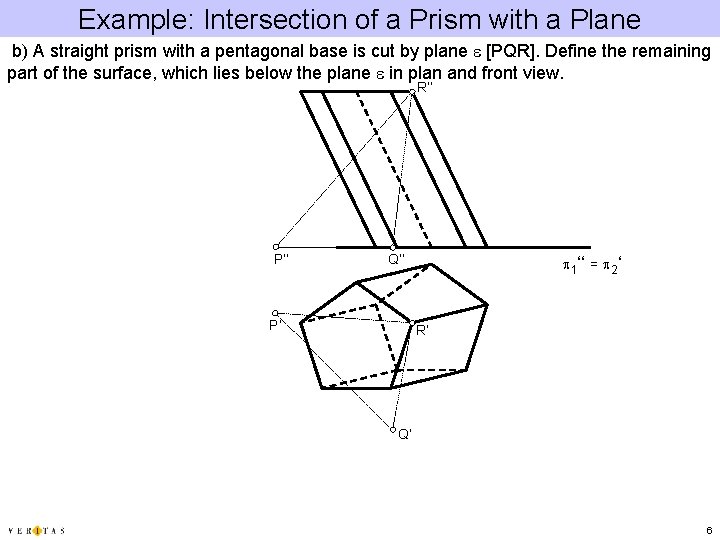
Example: Intersection of a Prism with a Plane b) A straight prism with a pentagonal base is cut by plane e [PQR]. Define the remaining part of the surface, which lies below the plane e in plan and front view. R‘‘ P‘‘ Q‘‘ P‘ p 1‘‘ = p 2‘ R‘ Q‘ 6

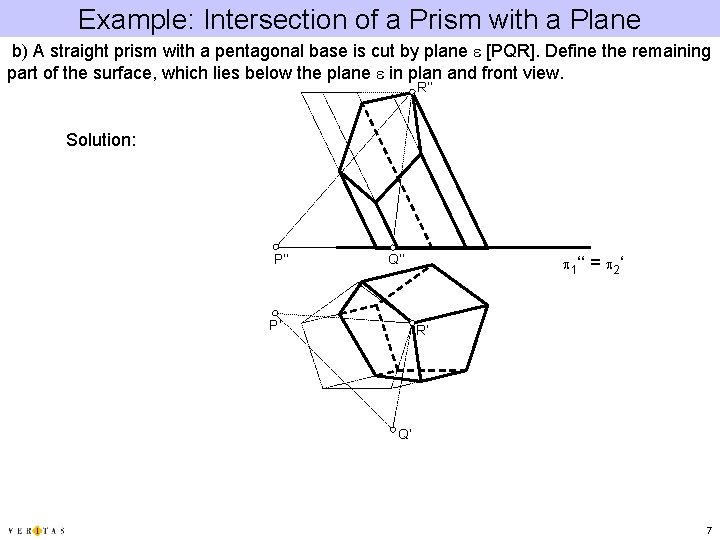
Example: Intersection of a Prism with a Plane b) A straight prism with a pentagonal base is cut by plane e [PQR]. Define the remaining part of the surface, which lies below the plane e in plan and front view. R‘‘ Solution: P‘‘ Q‘‘ P‘ p 1‘‘ = p 2 ‘ R‘ Q‘ 7