Example Harmonic Oscillator Estimate the minimum possible energy

Example: Harmonic Oscillator Estimate the minimum possible energy consistent with uncertainty principle (i. e. ground state energy) for a particle of mass m bound in a potential . Use x px /2 for uncertainty principle in this problem.

Let us imagine that the particle is confined to oscillate over a distance of the order of x. Classically if x is small the energy of the oscillator is small. Let us now assume that the particle is represented by a wave packet. Its physical dimension is limited to x. Hence like before, the confinement would cause an uncertainty in momentum and would lead to an average kinetic energy given to the particle.
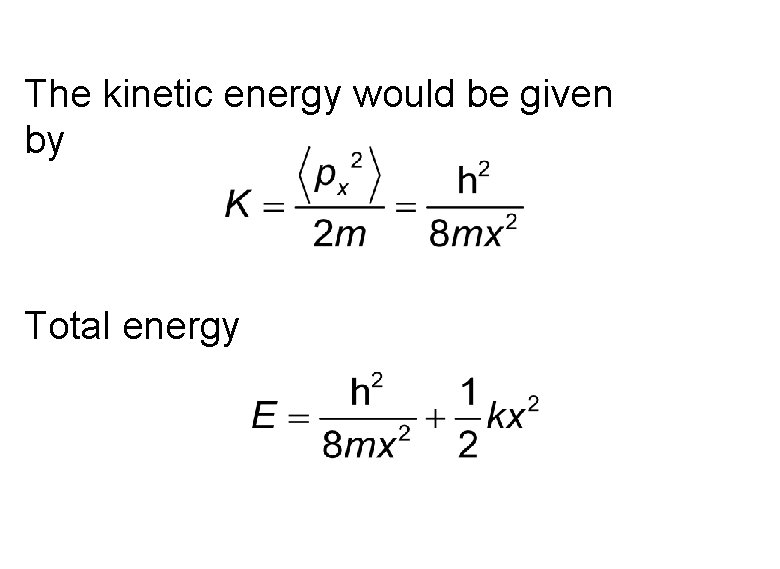
The kinetic energy would be given by Total energy
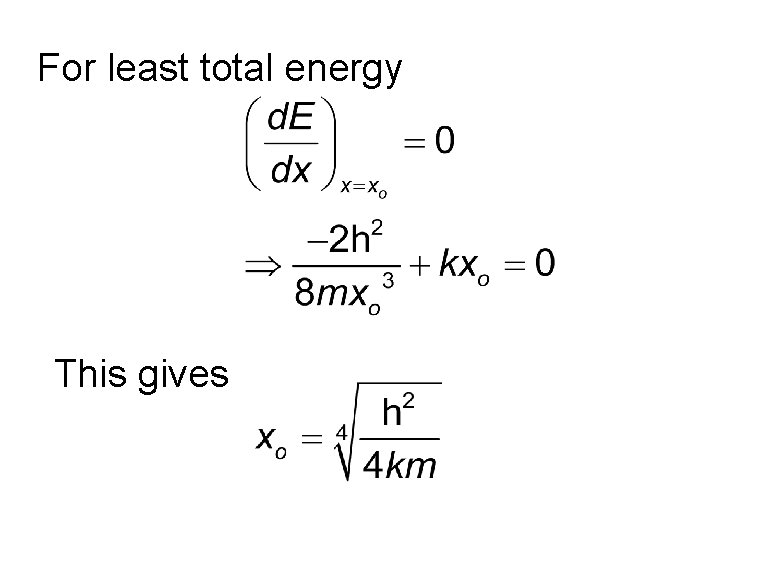
For least total energy This gives

Substituting back in the original expression we get Quantum Mechanics gives the same result.

Look-out for New Laws Classical Equations: 1. Particle 2. Wave

Question Which is the equation that governs a non-relativistic particle with observable wave behavior? The first one does not imply a wave nature at all. Second?

Various Forms to Represent Wave Following are the ways in which we can express a classical wave moving in +x direction. Do all these equations satisfy the wave
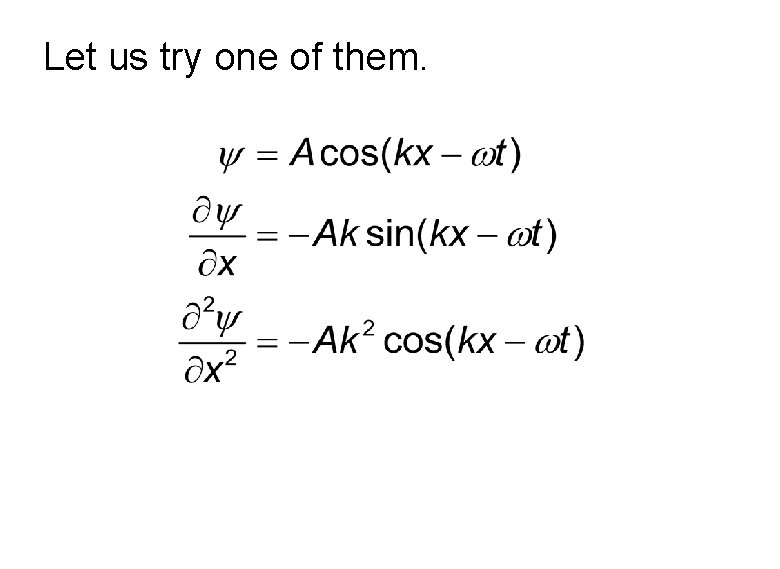
Let us try one of them.
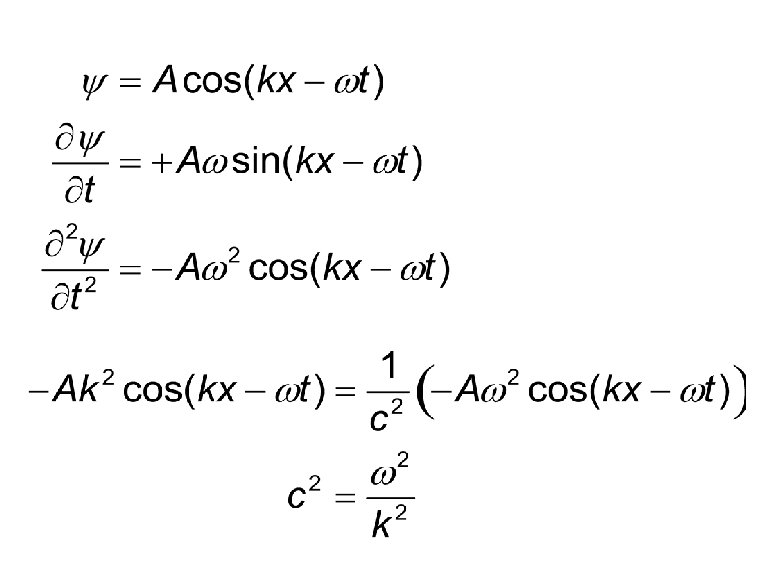
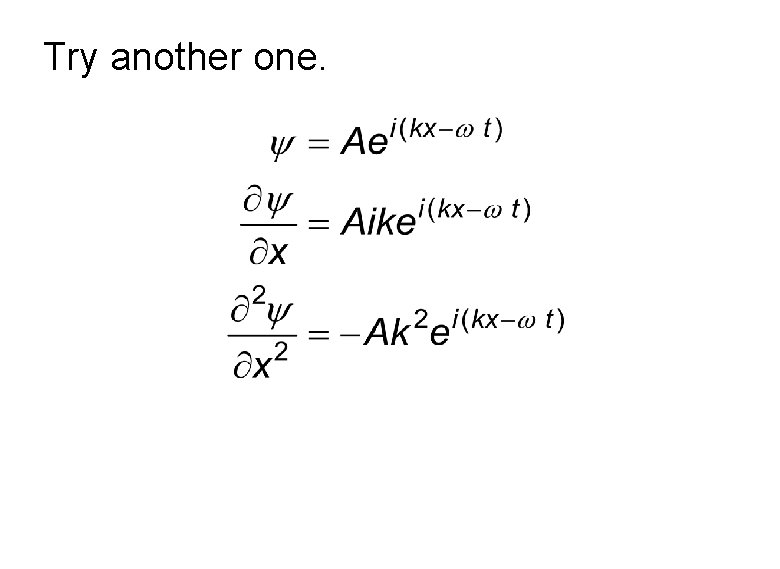
Try another one.
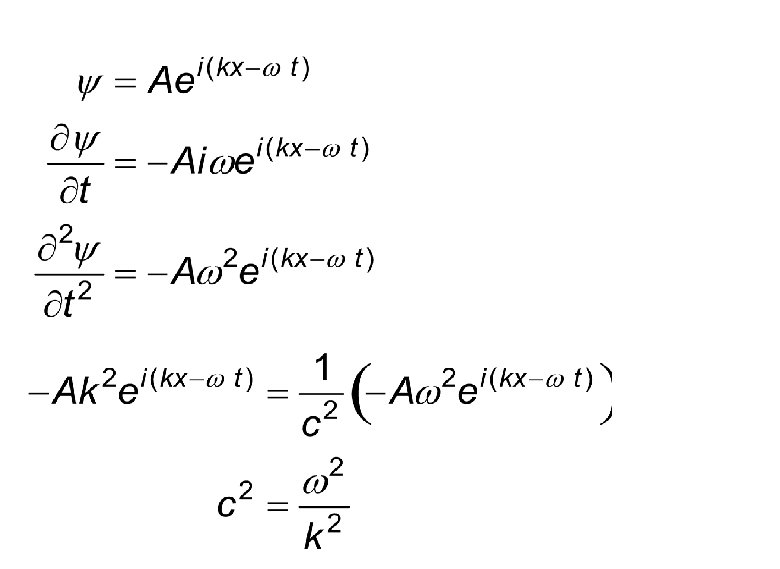

Superposition of Waves We know that electromagnetic waves even of different wavelengths superimpose. If we say that the wave equation is the wave governing the electromagnetic waves it implies that superposition should also be allowed.

If ψ1 and ψ2 are solutions of the wave equation, ψ1+ψ2 is also a solution of the wave equation. Let us verify it.

If ψ1 and ψ2 are solutions of the wave equation

We see that ψ1+ψ2 is also a solution of the wave equation. But note here c is same for both the waves

Is Superposition Possible for Particle? A particle can travel with any speed. In fact the wavelength of the particle depends on speed. If we take two particle waves, corresponding to same type of particle (e. g. electron), with different wavelengths, they would not superimpose, if the standard wave equation was governing it.

So can we form a wave packet? We probably need another equation.

How to Solve the Problem If the constant appearing in the wave equation was not dependent on dynamical properties like speed, momentum or energy, the superposition could have been valid.

Initially consider a non-relativistic free particle. For this particle we have the following relationship. Momentum can be related to k, while energy to ω.

If second derivative with x was related to the first derivative with t, things could be different. Why not try the following.

But are the standard displacement equation give by a pure trigonometric equation a solution of it? Traditionally we take the solution of the following form.
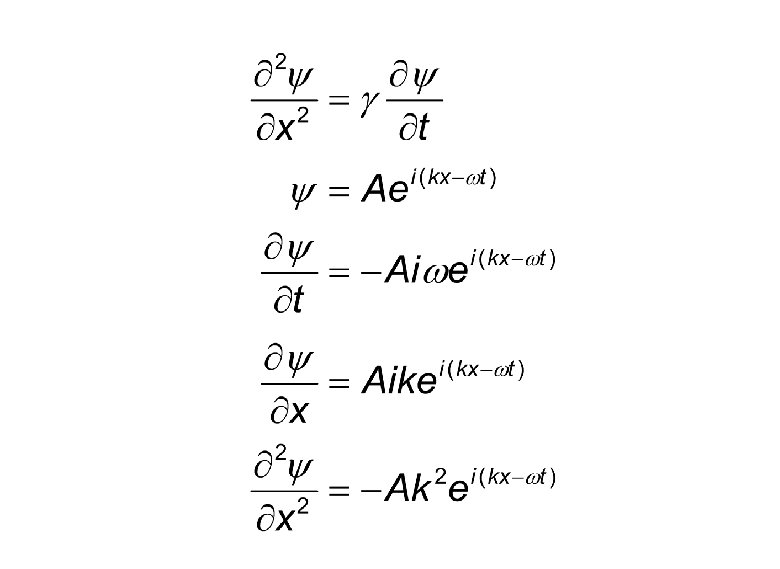
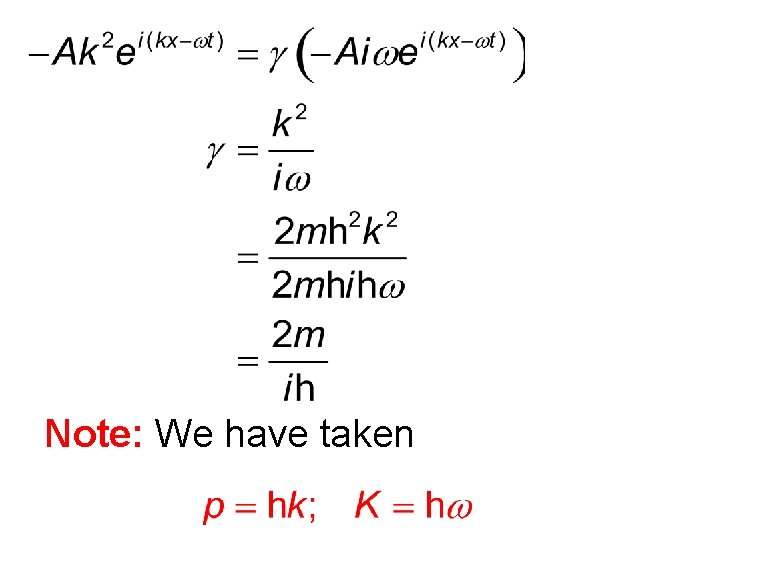
Note: We have taken
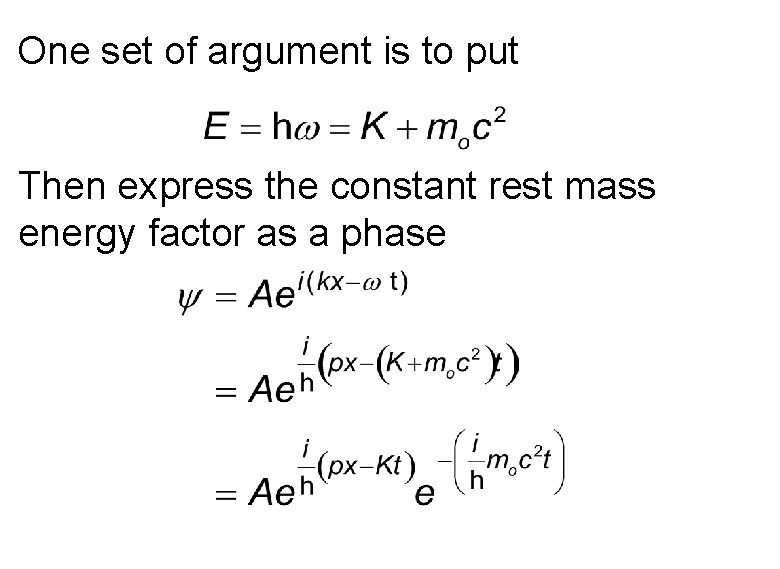
One set of argument is to put Then express the constant rest mass energy factor as a phase
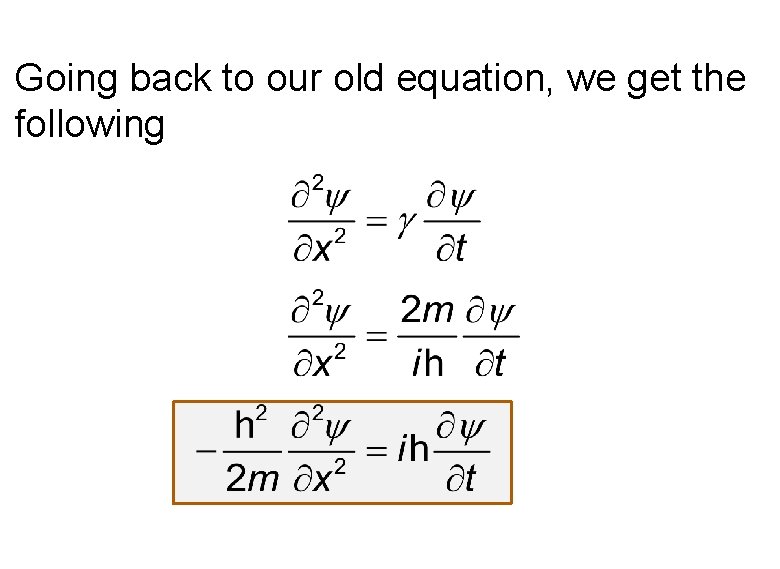
Going back to our old equation, we get the following

From now onwards we shall use in QM, K as the kinetic energy and E is the total non-relativistic energy, i. e. not including rest mass

Notes The value of γ indeed turned out to independent of dynamical variables, but depend on m. We could have also used for a wave travelling in +x direction.

Notes (Cond. ) In that case the value of γ would have changed sign. No Physics would have changed. Conventionally we use only the following.

Notes (Cond. ) The wave function turns out to be complex. But that shall not pose any problem so long the observables turn out to be real. We shall later see the physical interpretation of the wave function.

Operators Abstract but an essential component of QM. Are defined to maintain consistency with classical mechanics.

Momentum operator is defined the following way. This implies that

Energy Operator Energy operator is defined as Like before this implies that

Relook at the Old Equation

Schrödinger Equation Now we move our consideration from a free particle to particle under a force. For such a particle the following equation would be valid.

Multiply each side by ψ and replace relevant quantities by their operators, assuming one dimensional motion initially.

In General in three dimensions This is called Time Dependent Schrödinger Equation

Wave Function A microscopic particle is described by a wave function, which contains all the information that we can have about the physical properties of the particle. The Schrödinger Equation gives the position and time dependence of the wave function.

The probability of finding the particle between x and x+dx is given by

The Probability Imagine a very large number of separate identical particles described by the same wave function ψ(x, t). If a measurement of position is done on all of them at a time t, the result would not be identical. If the probability of finding particle between xo and x 1 is 0. 1, then in 10% of measurements the position would be found between xo and x 1.

The Probability is Not Defined over a measurement on a single particle. Suppose a measurement was made at a time t and the particle was found to be in the infinitesimal vicinity of xo. If we make a measurement immediately afterwards, it will still be found there. Experimental reproducibility is necessary. At a time much later, the wave function may again evolve under Schrödinger

Various Approaches If a measurement was done and the particle was found at x=xo , where was it just before? Realistic: Indeterminacy could be different from ignorance. The particle was there only, but we were not knowing. Some additional information was needed to provide the complete description (hidden variable)

Orthodox: The particle was not really there. Our method of measurement forced the particle to take a stand to be present (Copenhagen interpretation) Agnostic: Refuse to Answer Copenhagen interpretation is accepted one See D. J. Griffiths: Introduction to QM.

Normalization 1. If ψ is a solution the Aψ is also one. 2. The probability of finding the particle somewhere should be one. This in one -dimension would mean the following.

Normalization (Cond. ) In general, if dτ is the volume element in a given co-ordinate system Normalization would determine the unknown constant, within a phase factor

Normalization (Cond. ) Square integrability puts a condition on the wave function. The normalization is strictly not possible for a free wave, as the particle has equal probability of being found out over infinite space.
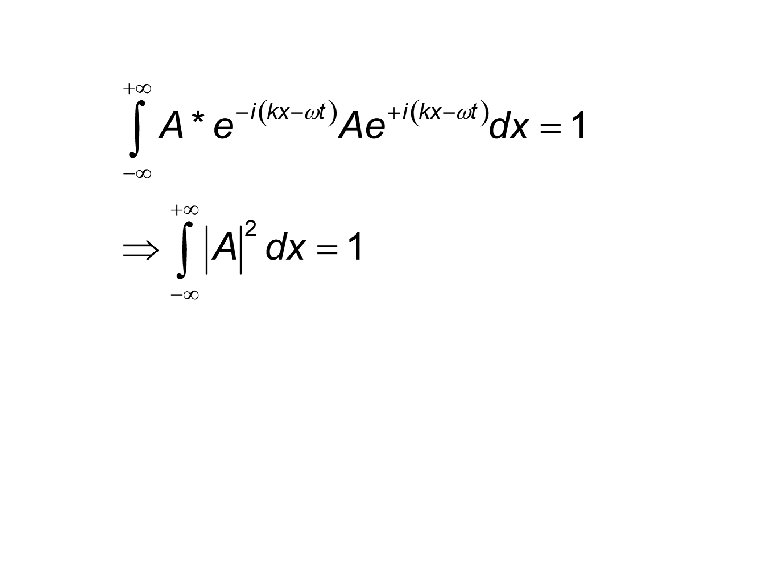

Example The wave function of a particle at t=0 is given by following.

Example (cond. ) A person performs N experiments on identical particles described by the same wave function and in 100 of them the particle was found to be in the infinitesimal vicinity of x=2 a. In how many of the measurements, it would be found in the same infinitesimal vicinity of x=a?
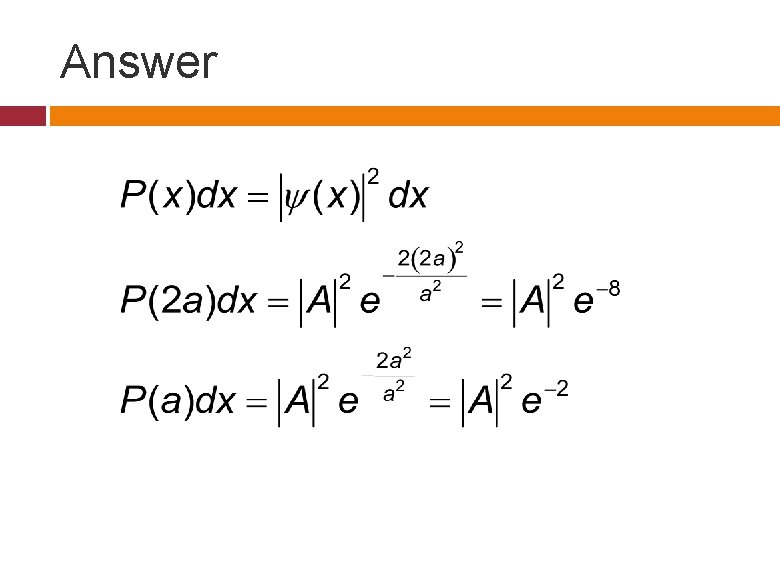
Answer
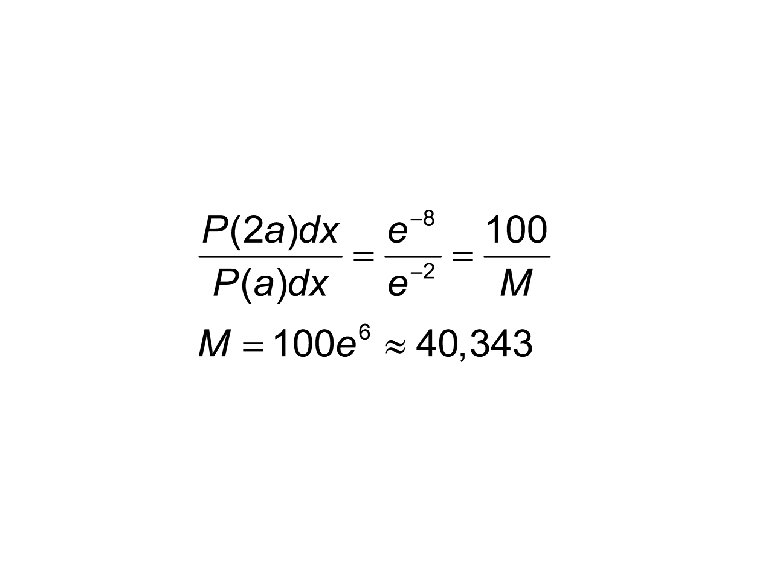
- Slides: 51