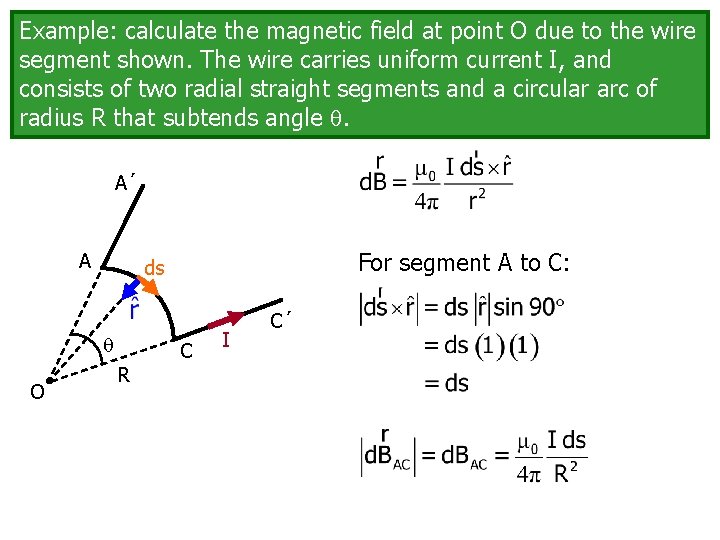
Example calculate the magnetic field at point O

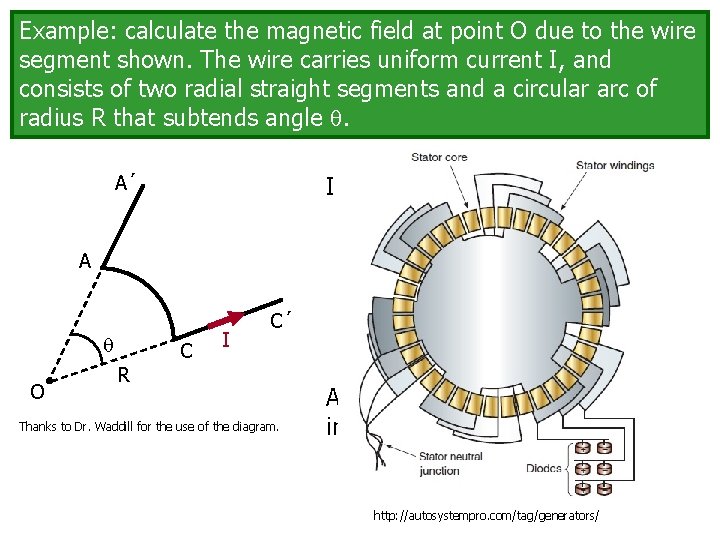
Example: calculate the magnetic field at point O due to the wire segment shown. The wire carries uniform current I, and consists of two radial straight segments and a circular arc of radius R that subtends angle . A´ I see three “parts” to the wire. A’ to A A A to C O C I C´ R Thanks to Dr. Waddill for the use of the diagram. C to C’ As usual, break the problem up into simpler parts. http: //autosystempro. com/tag/generators/

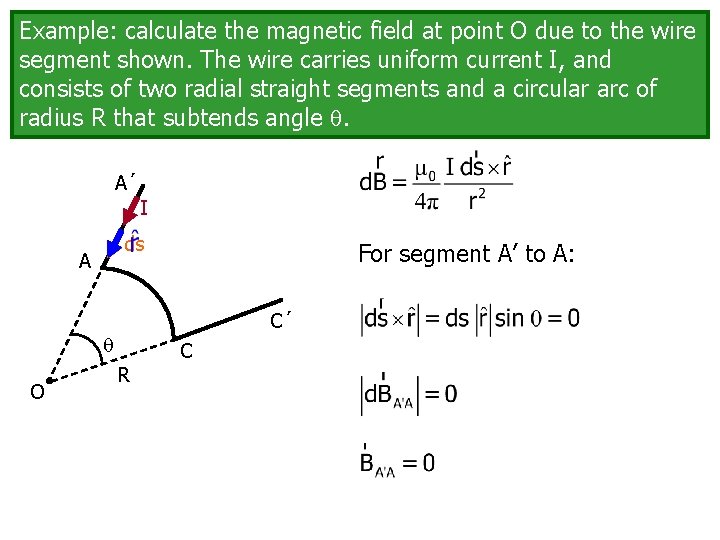
Example: calculate the magnetic field at point O due to the wire segment shown. The wire carries uniform current I, and consists of two radial straight segments and a circular arc of radius R that subtends angle . A´ I ds A For segment A’ to A: C´ O C R

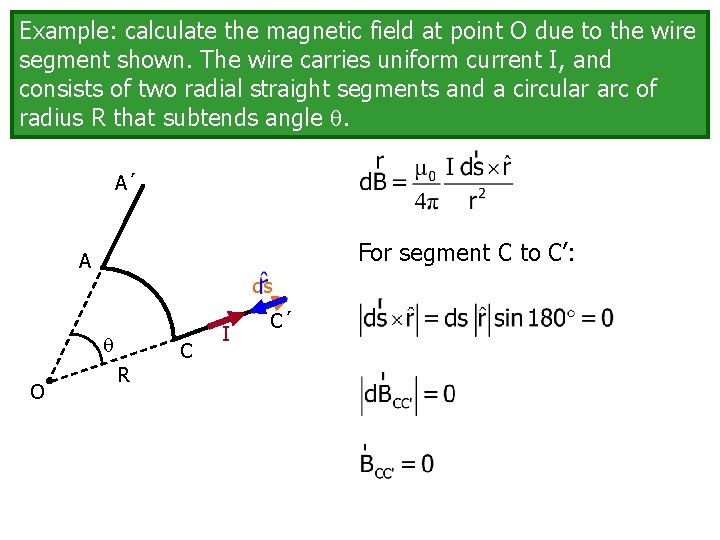
Example: calculate the magnetic field at point O due to the wire segment shown. The wire carries uniform current I, and consists of two radial straight segments and a circular arc of radius R that subtends angle . A´ For segment C to C’: A ds O C R I C´

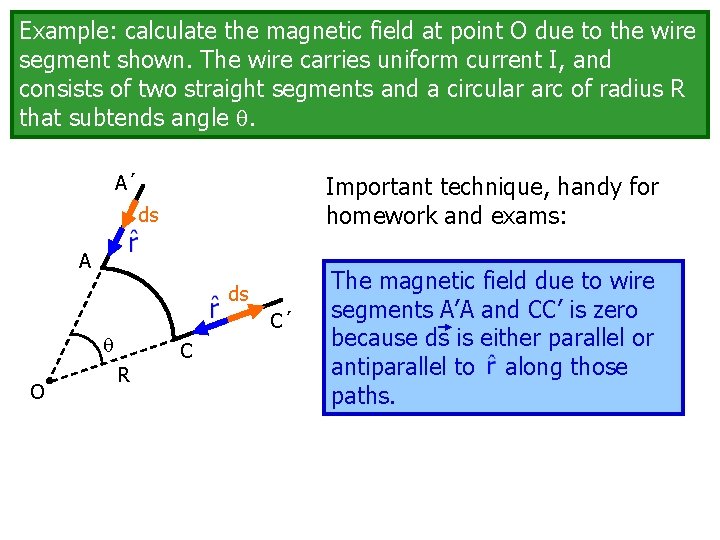
Example: calculate the magnetic field at point O due to the wire segment shown. The wire carries uniform current I, and consists of two straight segments and a circular arc of radius R that subtends angle . A´ Important technique, handy for homework and exams: ds A ds C´ O C R The magnetic field due to wire segments A’A and CC’ is zero because ds is either parallel or antiparallel to along those paths.

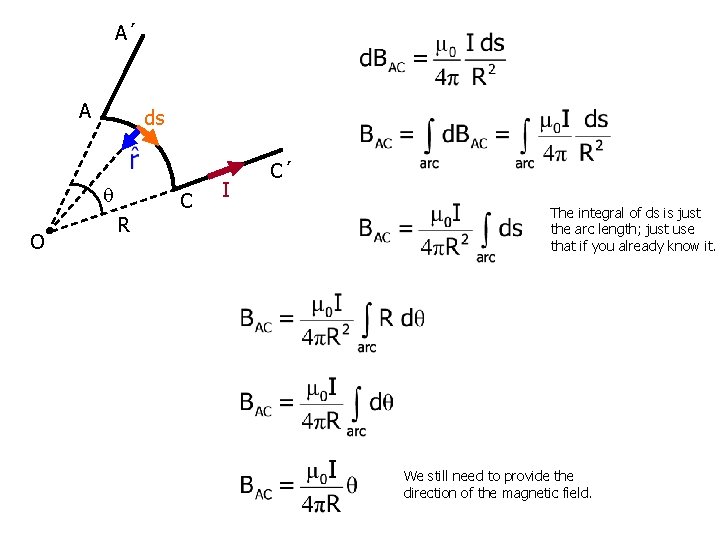
Example: calculate the magnetic field at point O due to the wire segment shown. The wire carries uniform current I, and consists of two radial straight segments and a circular arc of radius R that subtends angle . A´ A O For segment A to C: ds C R I C´

A´ A ds O C R I C´ The integral of ds is just the arc length; just use that if you already know it. We still need to provide the direction of the magnetic field.

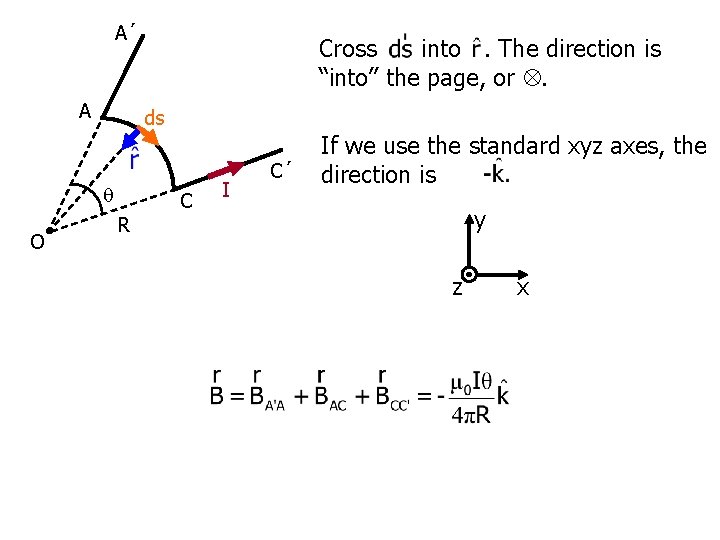
A´ A ds O Cross into. The direction is “into” the page, or . C I C´ If we use the standard xyz axes, the direction is y R z x

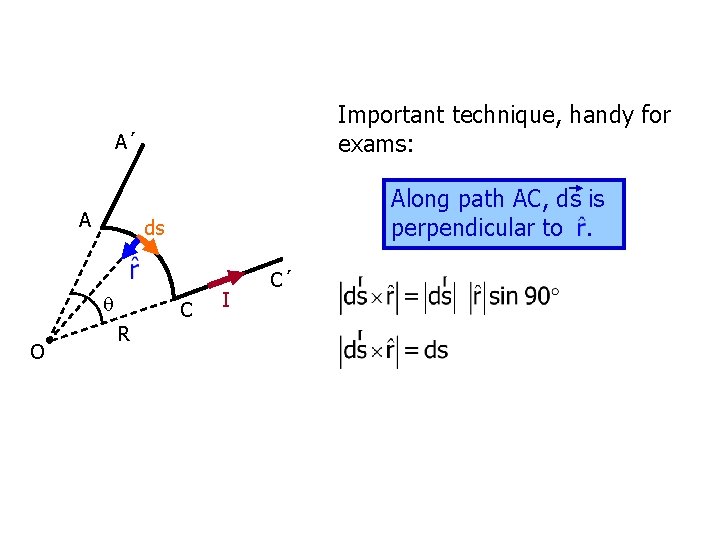
Important technique, handy for exams: A´ A ds O Along path AC, ds is perpendicular to. C R I C´