Example calculate the electric field at center of

Example: calculate the electric field at “center” of semicircular line of uniformly-distributed positive charge, oriented as shown. +Q R y You don’t have to follow the steps in the exact order I present here. Just let the problem tell you what to. You may do things in a different order; that’s probably OK. x ds To be worked at the blackboard in lecture. d R d. E

Example: calculate the electric field at “center” of semicircular line of uniformly-distributed positive charge, oriented as shown. +Q dq ds d y Start with our usual OSE. R x Pick an infinitesimal dq of charge. dq subtends an arc length ds, and an angle d. What is the charge dq?

Example: calculate the electric field at “center” of semicircular line of uniformly-distributed positive charge, oriented as shown. +Q dq ds d y xd. E′ dq′ R d. E Draw the d. E due to the dq, and show its components. Do you see any helpful symmetry? Pick a dq′ horizontally across the arc from dq. The xcomponents of dq and dq′ will cancel. Because of this symmetry, Ex = 0 Each d. Ey points downward so Ey will be negative.

Example: calculate the electric field at “center” of semicircular line of uniformly-distributed positive charge, oriented as shown. +Q dq ds dq y x R d. E Recall that dq and ds are infinitesimal. dq is located at an angle along the semicircle from the negative y-axis. is also one of the angles in the vector triangle.

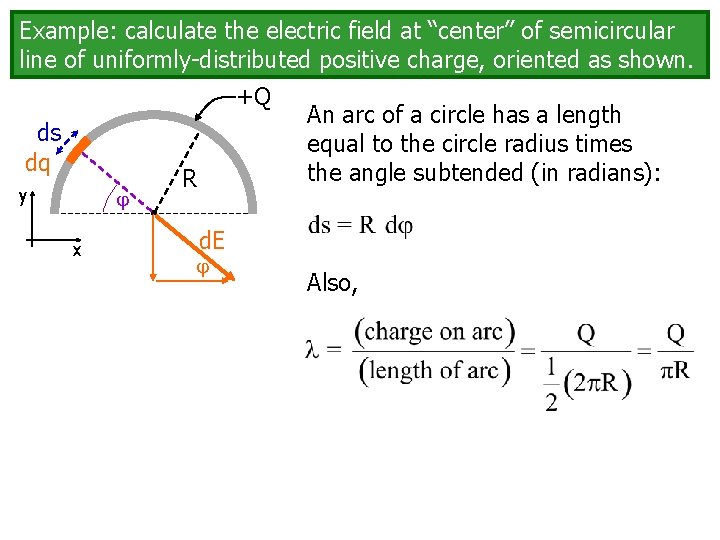
Example: calculate the electric field at “center” of semicircular line of uniformly-distributed positive charge, oriented as shown. +Q dq ds dq y x R An arc of a circle has a length equal to the circle radius times the angle subtended (in radians): d. E Also,

+Q dq ds dq y x Let’s summarize what we have done so far. R d. E Every dq is a distance R away from the arc center:

+Q dq ds dq y x R d. E Awesome Youtube derivation: http: //www. youtube. com/watch? v=L 1 n 2 EUvayfw