Example 8 Puzzle State Space 1 initial state

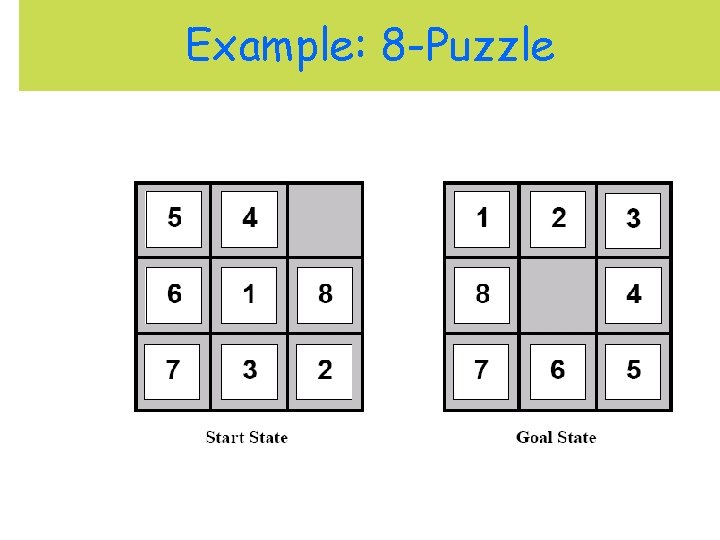
Example: 8 -Puzzle

State Space 1. initial state 2. successor function

Goal Test 3. goal test

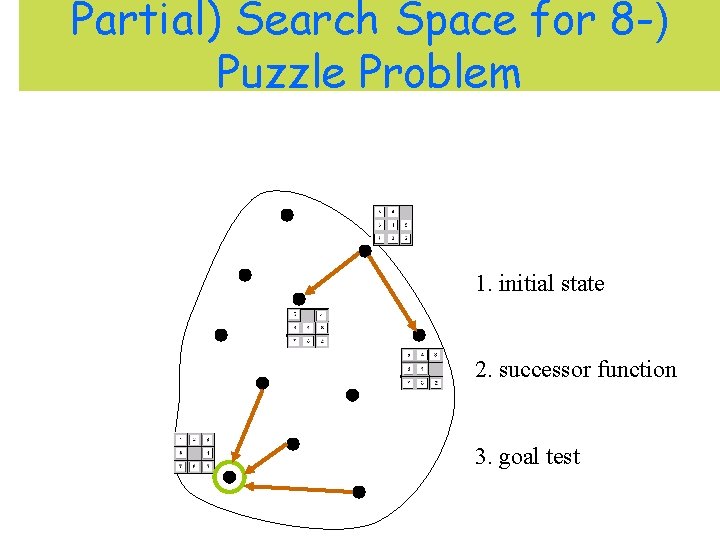
Partial) Search Space for 8 -) Puzzle Problem 1. initial state 2. successor function 3. goal test

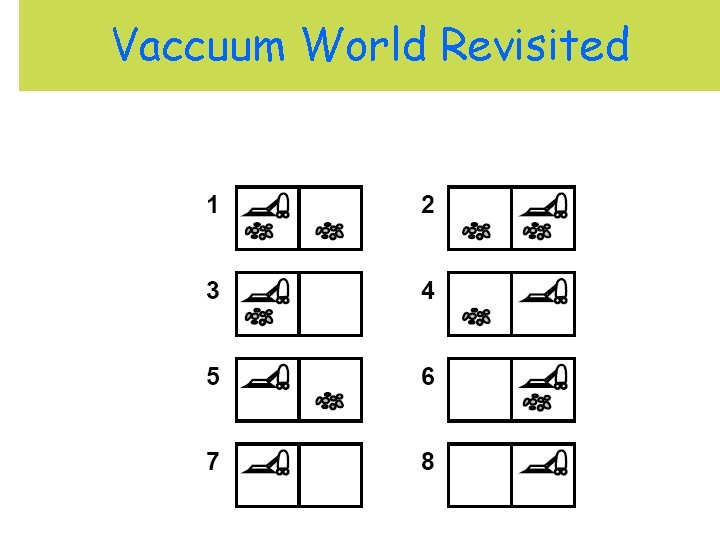
Vaccuum World Revisited

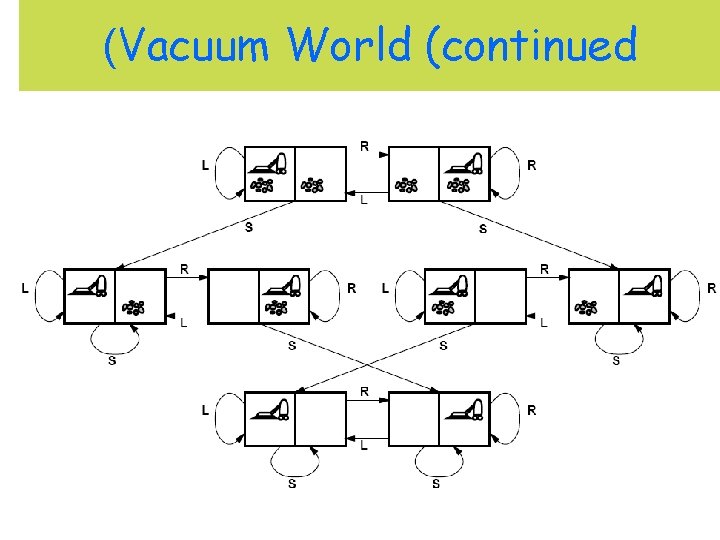
(Vacuum World (continued

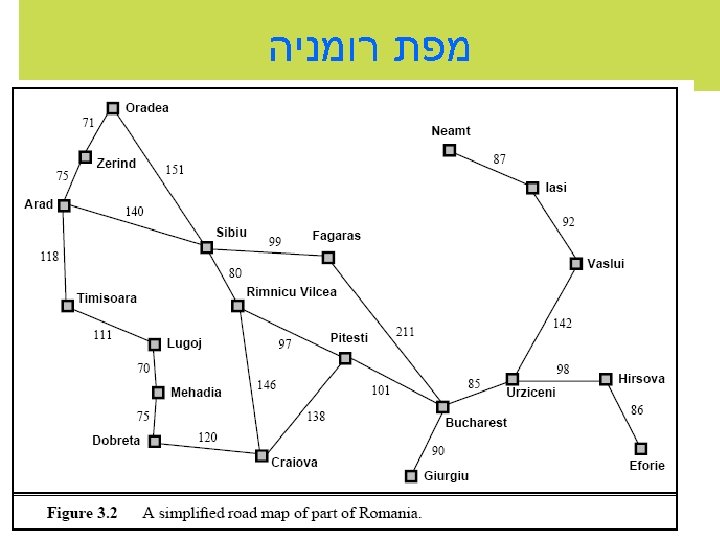
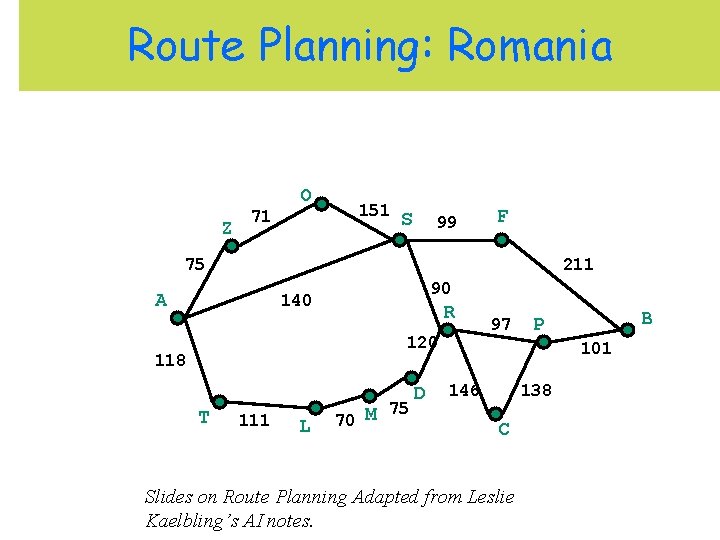
Example: Route Planning in a Map Graph: nodes are cities and links are roads. • Map gives world dynamics • Current state is known • World is fully predictable • World (set of cities) is finite and enumerable. Cost: total distance or total time for path.

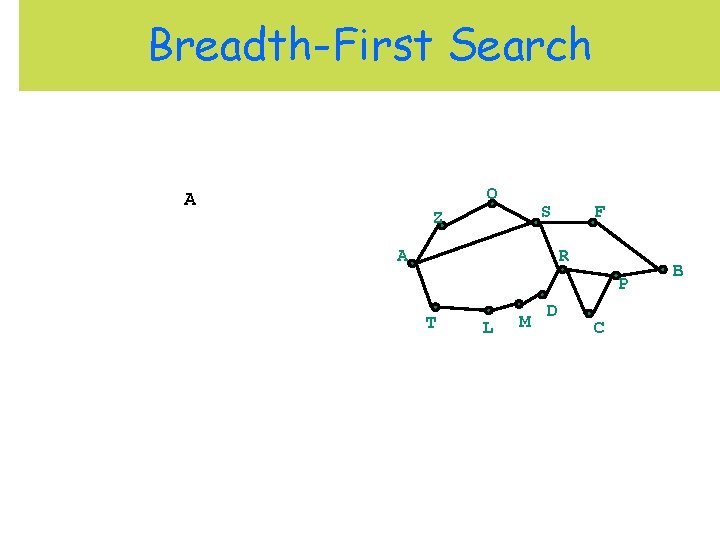
Route Planning: Romania Z 71 O 151 S 99 F 75 211 A 90 140 R 120 118 T 111 L 75 70 M D 97 B P 101 146 138 C Slides on Route Planning Adapted from Leslie Kaelbling’s AI notes.

General Search-Tree Algorithm

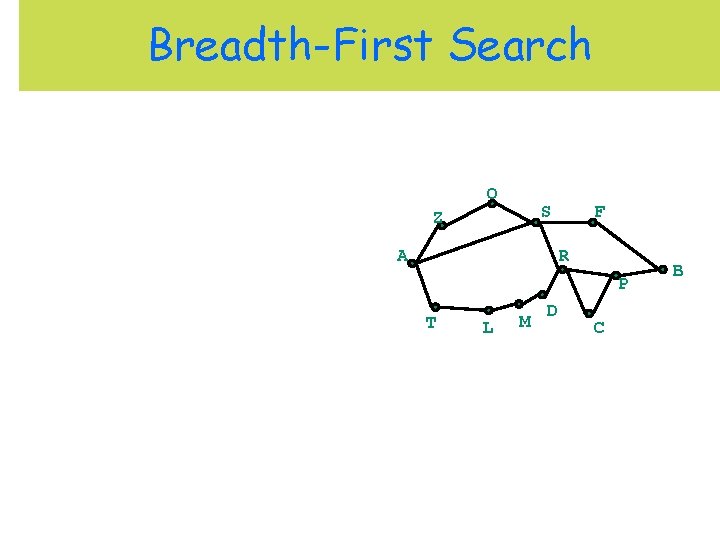
Breadth-First Search O S Z A F R P T L M D C B

Breadth-First Search O A S Z A F R P T L M D C B

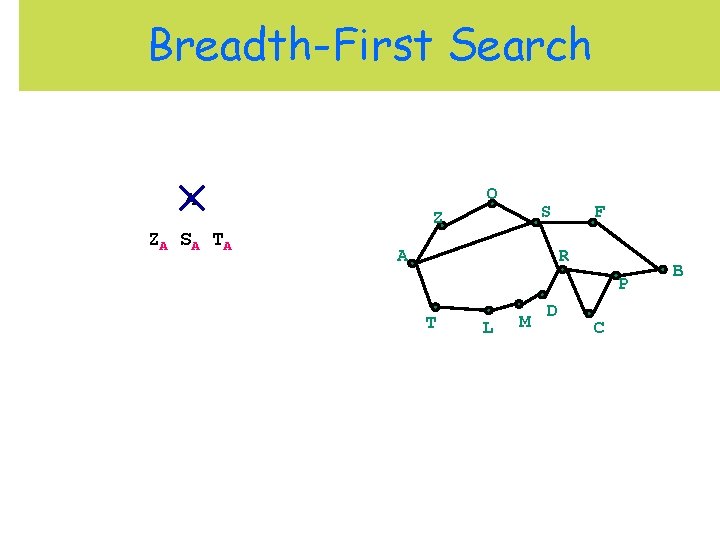
Breadth-First Search O A ZA S A T A S Z A F R P T L M D C B

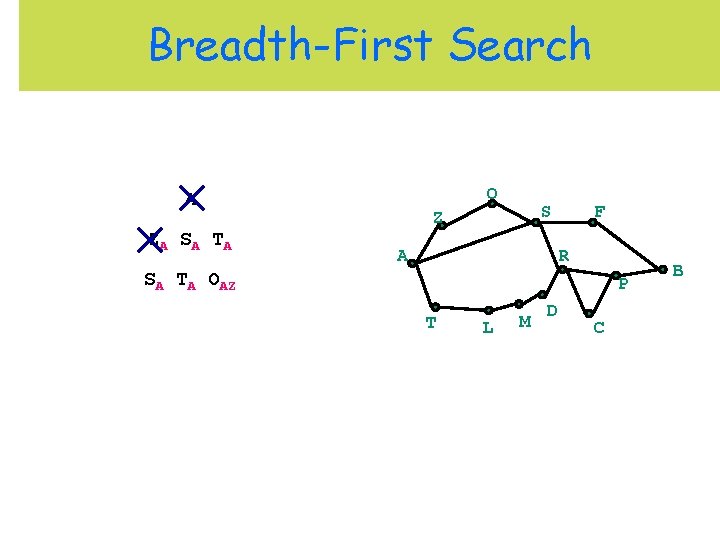
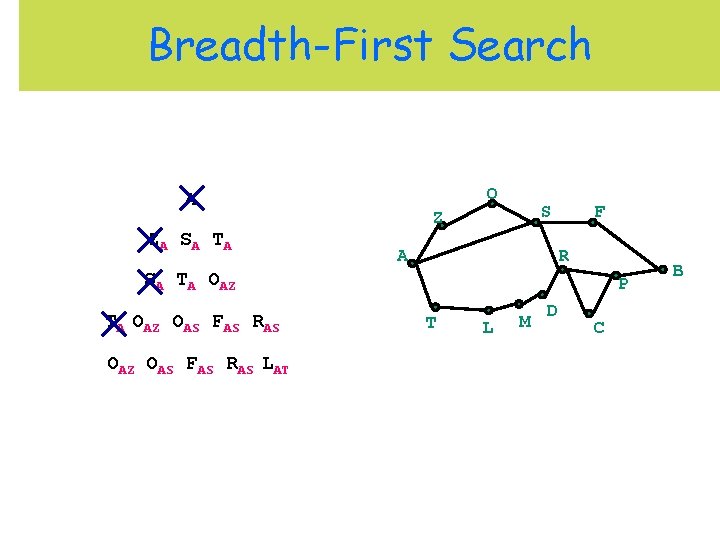
Breadth-First Search O A ZA S A T A S Z A F R SA TA OAZ P T L M D C B

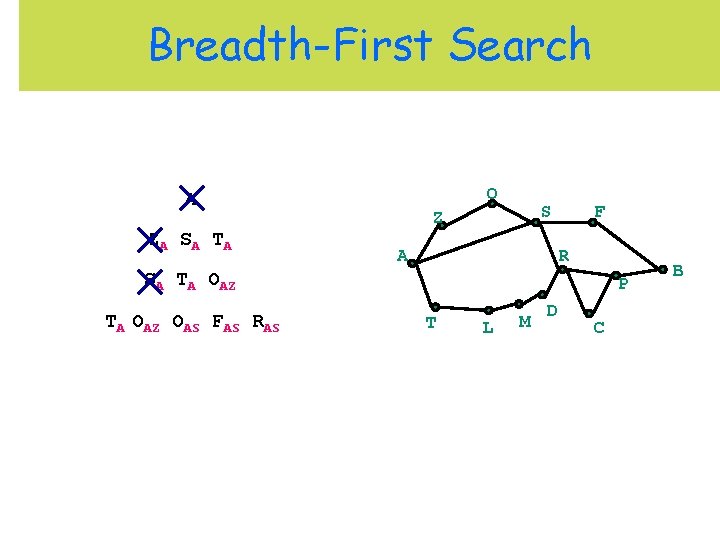
Breadth-First Search O A ZA S A T A S Z A F R SA TA OAZ OAS FAS RAS P T L M D C B

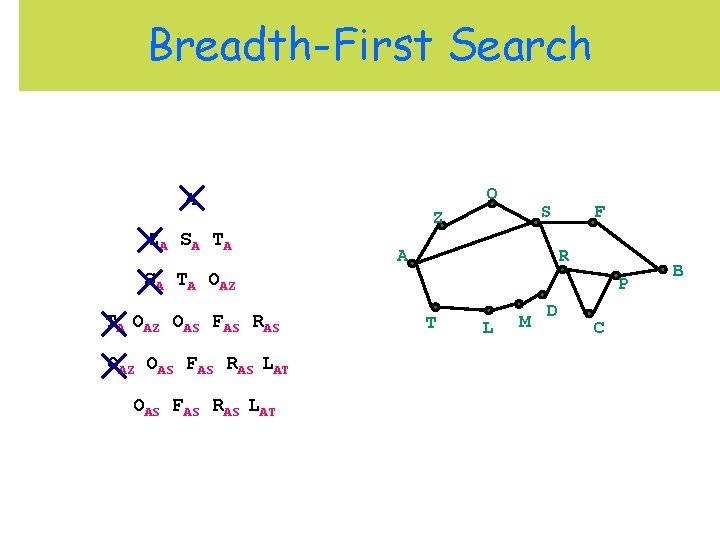
Breadth-First Search O A ZA S A T A S Z A F R SA TA OAZ OAS FAS RAS LAT P T L M D C B

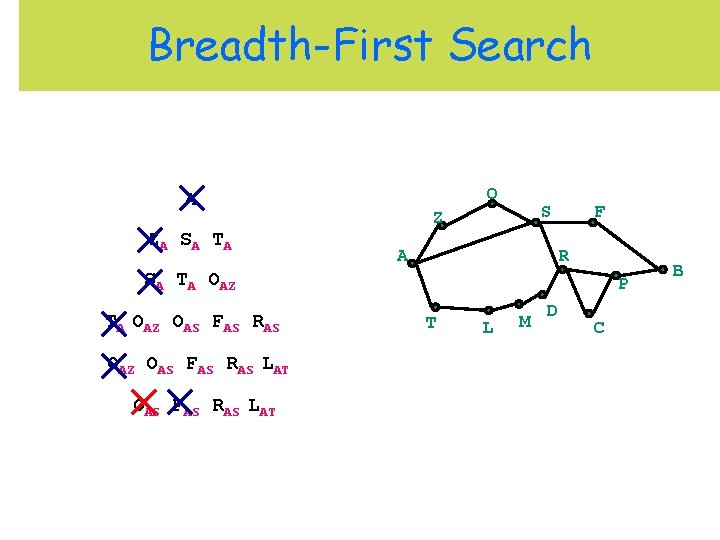
Breadth-First Search O A ZA S A T A S Z A F R SA TA OAZ OAS FAS RAS LAT P T L M D C B

Breadth-First Search O A ZA S A T A S Z A F R SA TA OAZ OAS FAS RAS LAT P T L M D C B

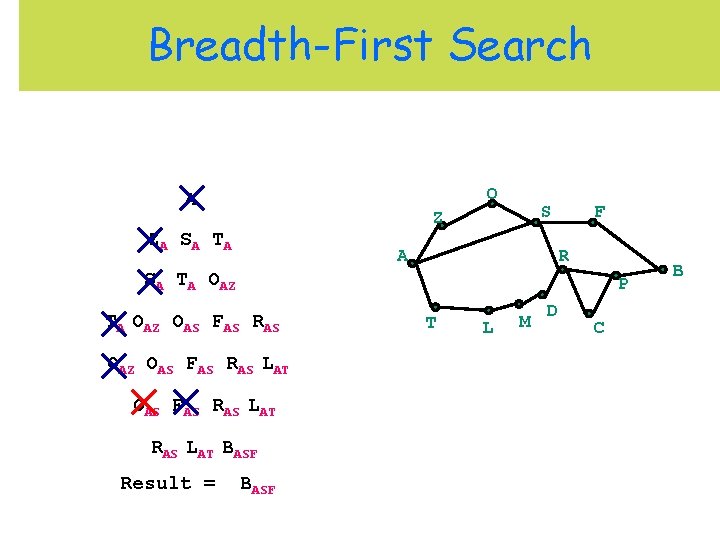
Breadth-First Search O A S Z ZA S A T A A F R SA TA OAZ P TA OAZ OAS FAS RAS LAT BASF Result = BASF T L M D C B

Breadth-First Search O S Z A F R B P T L M D C

Evaluation of Search Strategies • • Completeness Time Complexity Space Complexity Optimality To evaluate, we use the following terms • b = branching factor • m = maximum depth • d = goal depth

Evaluation of BFS • Complete • Complexity: – O(bd) time – O(bd) space • Optimal (counting by number of arcs).

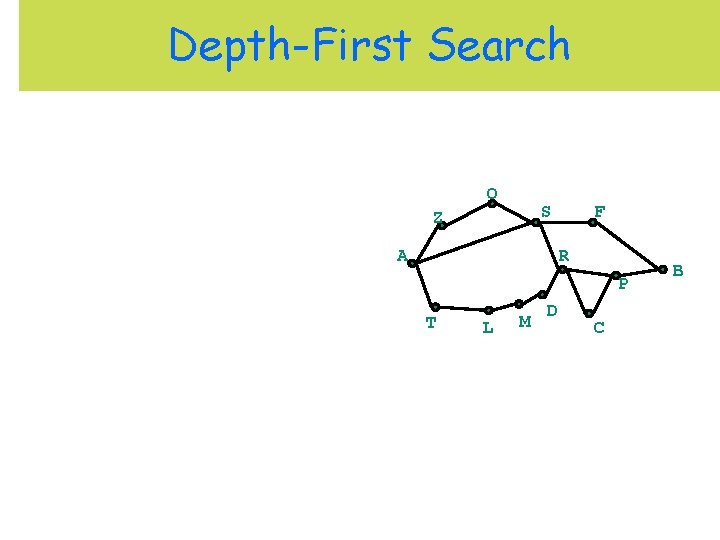
Depth-First Search O S Z A F R P T L M D C B

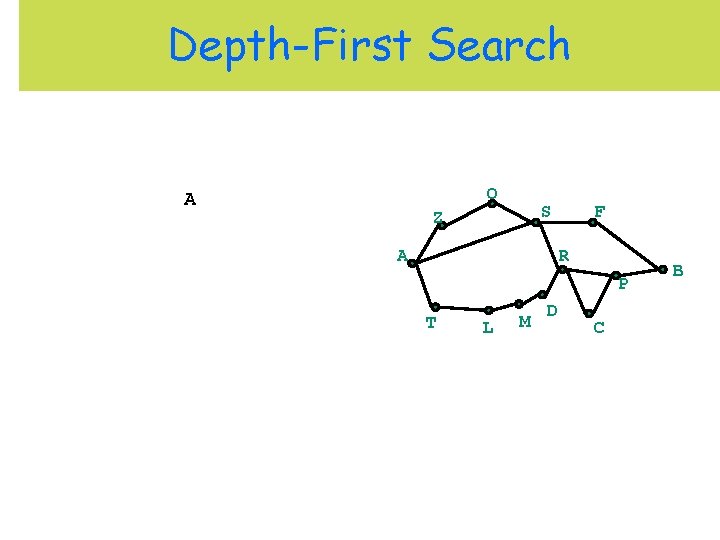
Depth-First Search O A S Z A F R P T L M D C B

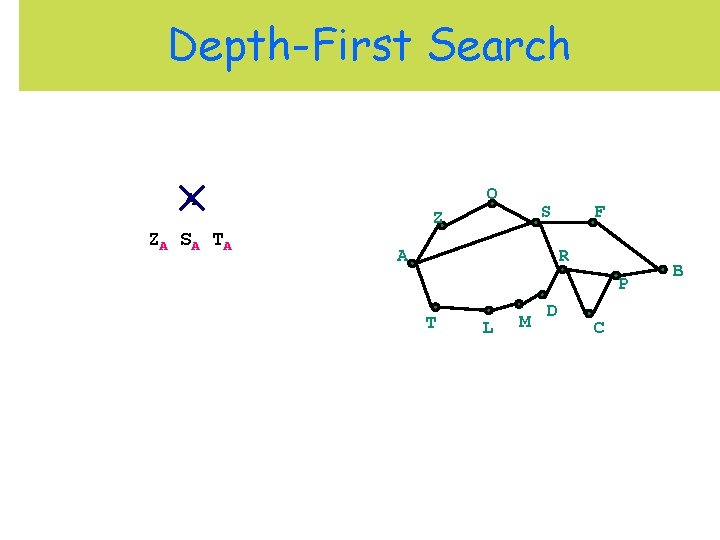
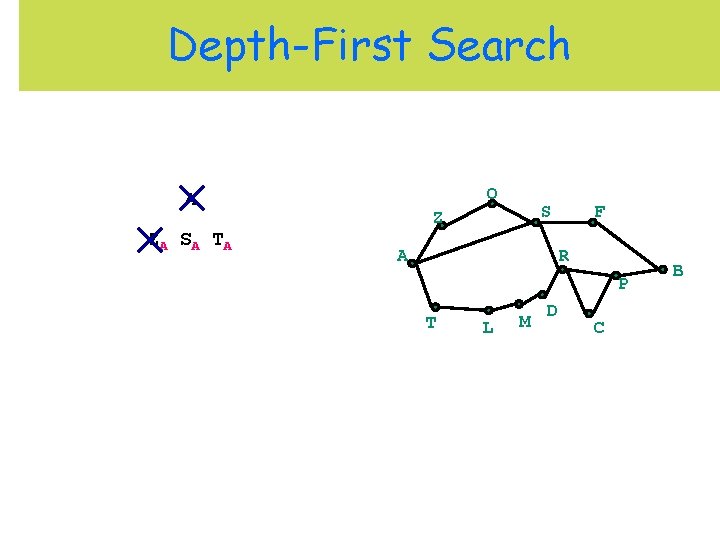
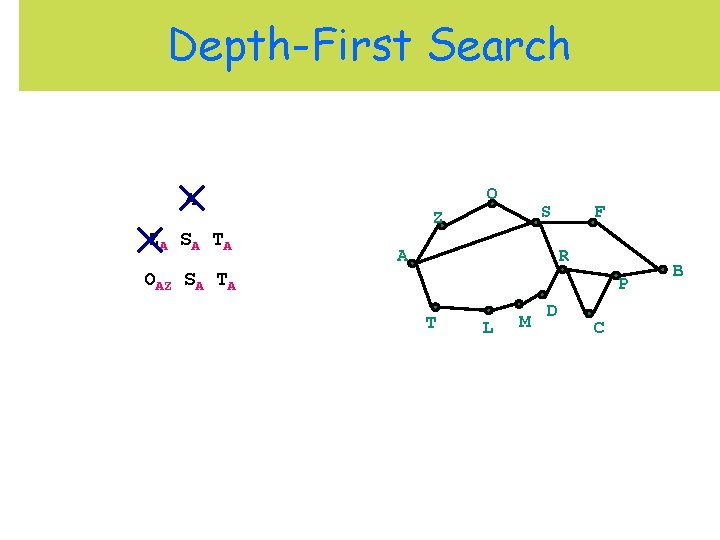
Depth-First Search O A ZA S A T A S Z A F R P T L M D C B

Depth-First Search O A ZA S A T A S Z A F R P T L M D C B

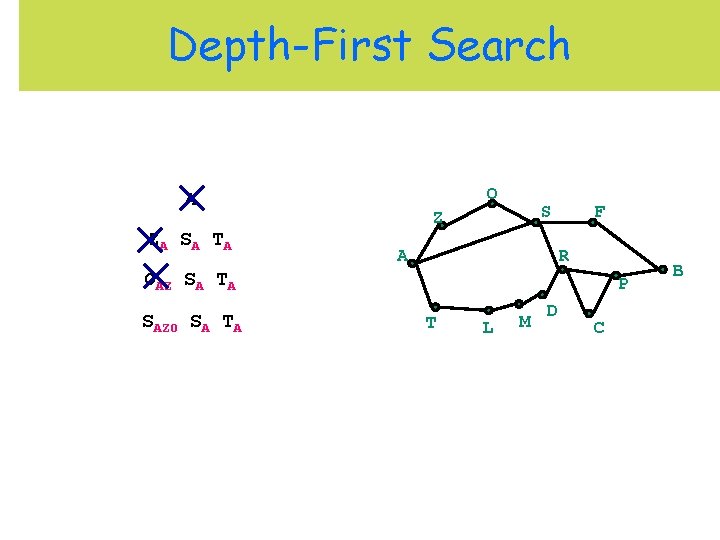
Depth-First Search O A ZA S A T A S Z A F R OAZ SA TA P T L M D C B

Depth-First Search O A ZA S A T A S Z A F R OAZ SA TA SAZO SA TA P T L M D C B

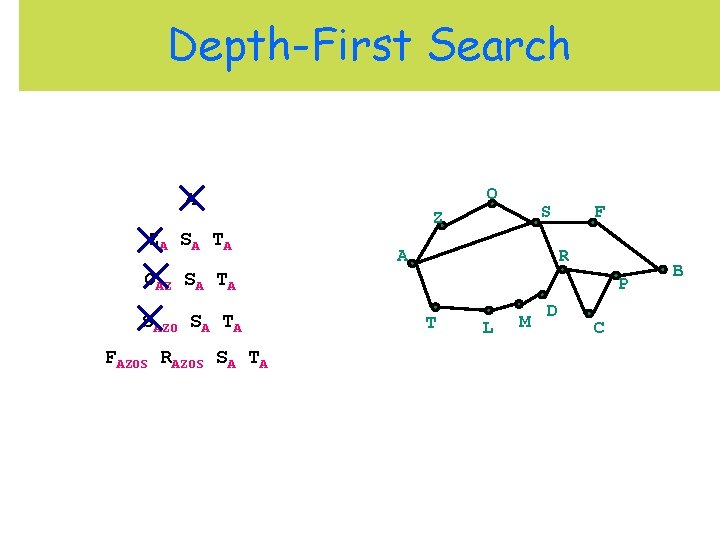
Depth-First Search O A ZA S A T A S Z A F R OAZ SA TA SAZO SA TA FAZOS RAZOS SA TA P T L M D C B

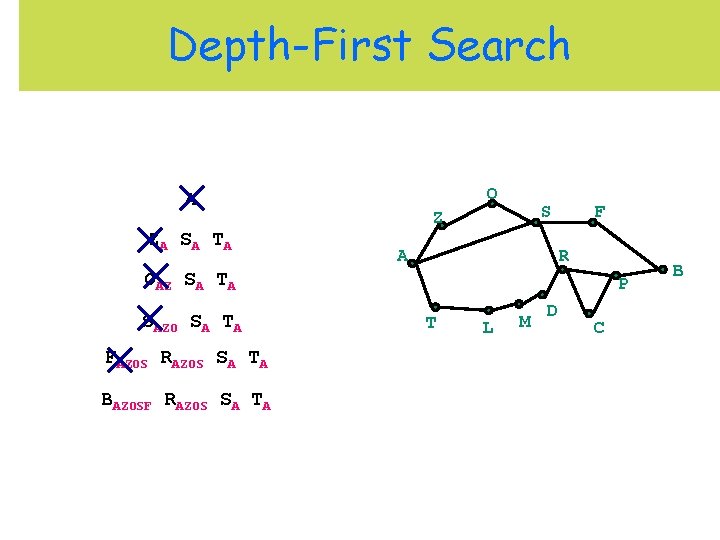
Depth-First Search O A ZA S A T A S Z A F R OAZ SA TA SAZO SA TA FAZOS RAZOS SA TA BAZOSF RAZOS SA TA P T L M D C B

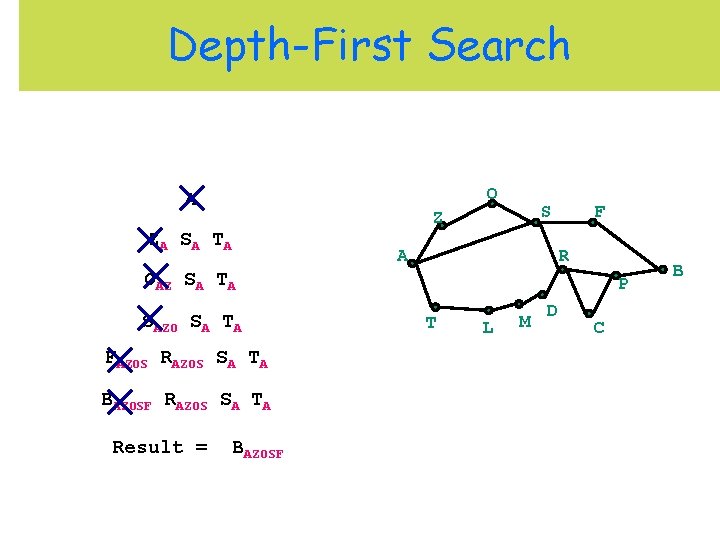
Depth-First Search O A S Z ZA S A T A A F R OAZ SA TA SAZO SA TA FAZOS RAZOS SA TA BAZOSF RAZOS SA TA Result = BAZOSF P T L M D C B

Depth-first Search O S Z A F R B P T L M D C

Evaluation of DFS • Not complete • Complexity: – O(bm) time – O(mb) space • Non-optimal

Lisp Implementation (defun tree-search (states goal-successors combiner) "Find a state that satisfies goal-p. Start with states, and search according to successors and combiner. " (cond ((null states) fail) ((funcall goal-p (first states)) (t (tree-search (funcall combiner (funcall successors (first states)) (rest states)) goal-p successors combiner))))