Example 6 10 Determine the maximum positive moment

  • Slides: 26
Download presentation
Example 6 -10 Determine the maximum positive moment and negative moment created at point

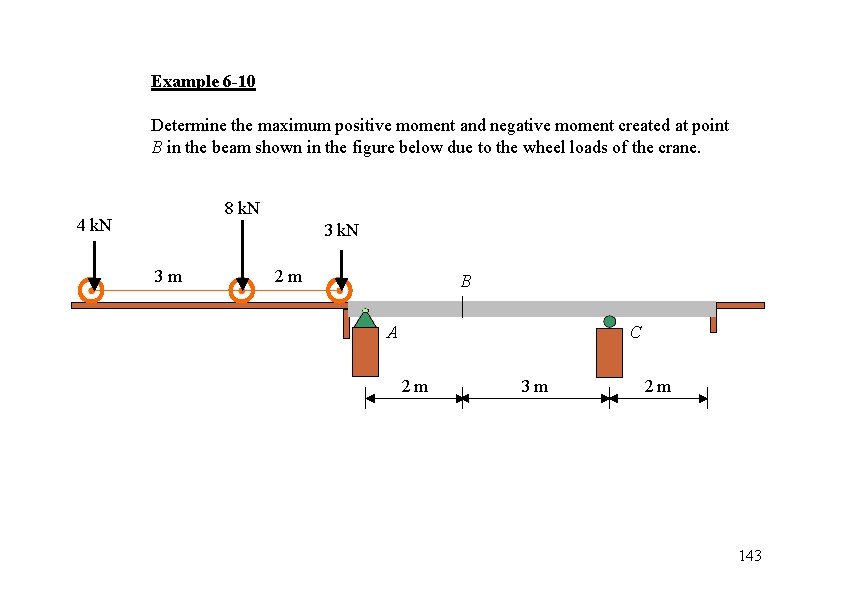
Example 6 -10 Determine the maximum positive moment and negative moment created at point B in the beam shown in the figure below due to the wheel loads of the crane. 8 k. N 4 k. N 3 m 2 m B A C 2 m 3 m 2 m 143

SOLUTION • Positive moment 4 k. N 8 k. N 3 m 2 m

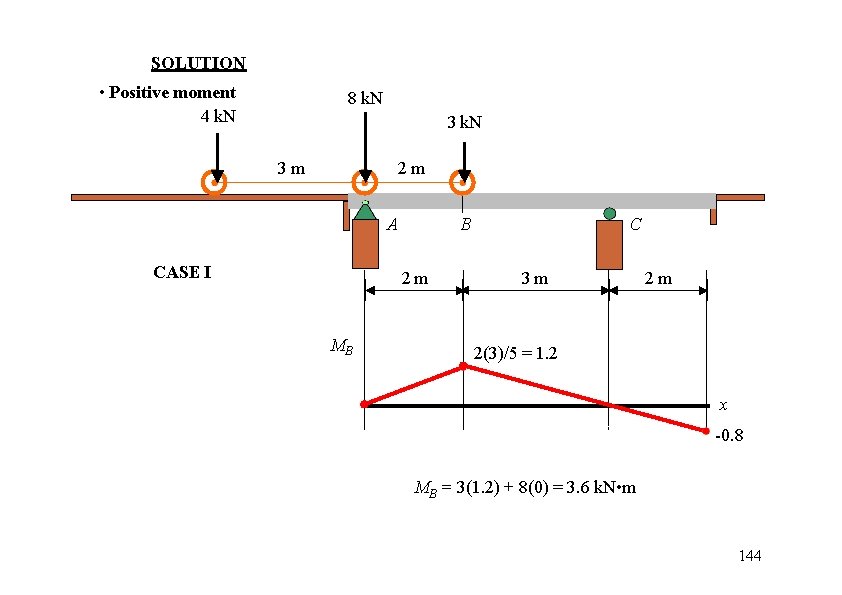
SOLUTION • Positive moment 4 k. N 8 k. N 3 m 2 m A CASE I B 2 m MB C 3 m 2 m 2(3)/5 = 1. 2 x -0. 8 MB = 3(1. 2) + 8(0) = 3. 6 k. N • m 144

8 k. N 4 k. N 3 m 2 m A CASE II B

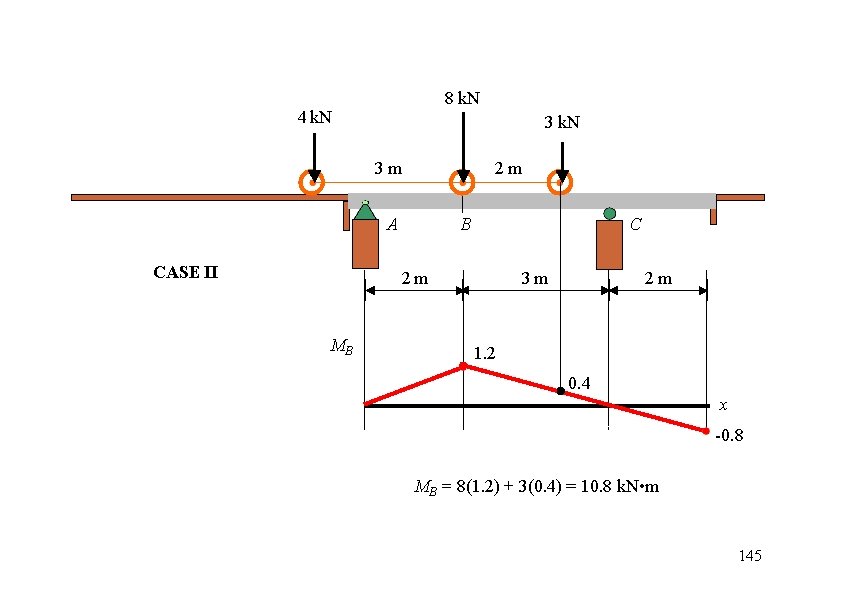
8 k. N 4 k. N 3 m 2 m A CASE II B C 2 m MB 3 m 2 m 1. 2 0. 4 x -0. 8 MB = 8(1. 2) + 3(0. 4) = 10. 8 k. N • m 145

8 k. N 4 k. N 3 m A CASE III B C 2

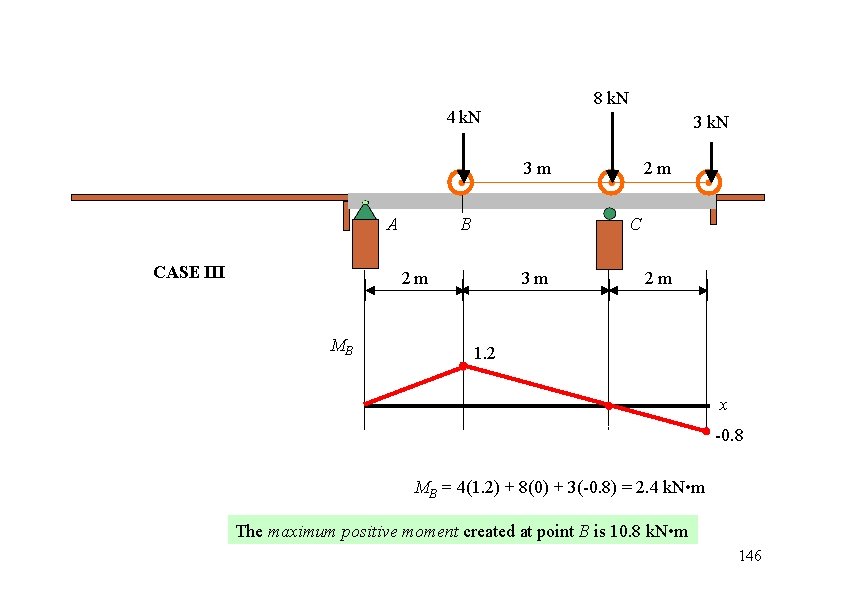
8 k. N 4 k. N 3 m A CASE III B C 2 m MB 2 m 3 m 2 m 1. 2 x -0. 8 MB = 4(1. 2) + 8(0) + 3(-0. 8) = 2. 4 k. N • m The maximum positive moment created at point B is 10. 8 k. N • m 146

• Negative moment 8 k. N 4 k. N 3 m A B

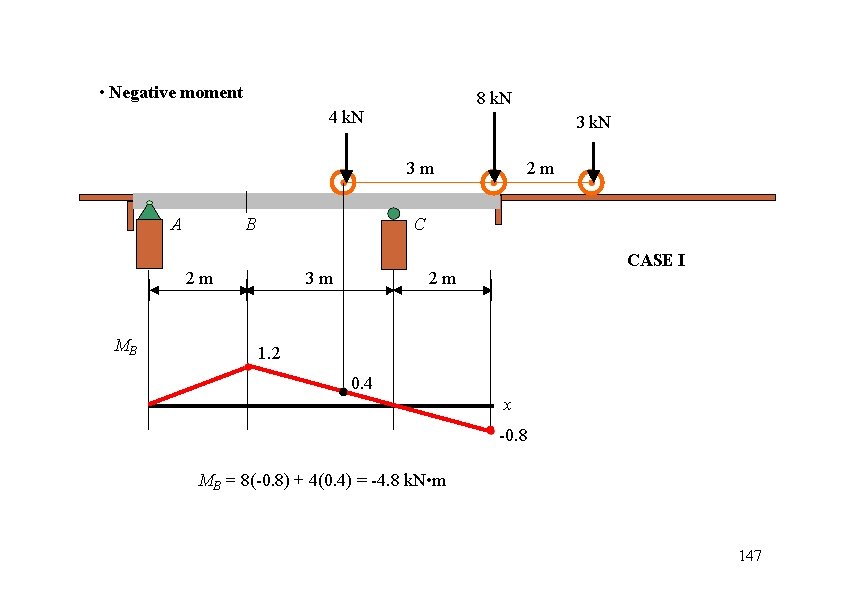
• Negative moment 8 k. N 4 k. N 3 m A B C 2 m MB 2 m 3 m CASE I 2 m 1. 2 0. 4 x -0. 8 MB = 8(-0. 8) + 4(0. 4) = -4. 8 k. N • m 147

8 k. N 4 k. N 3 m A B C 2 m MB

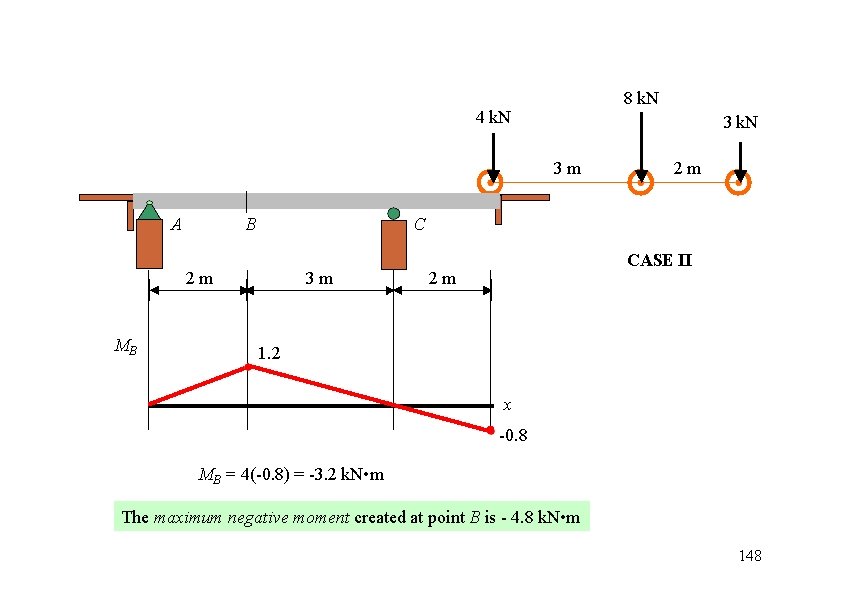
8 k. N 4 k. N 3 m A B C 2 m MB 2 m 3 m CASE II 2 m 1. 2 x -0. 8 MB = 4(-0. 8) = -3. 2 k. N • m The maximum negative moment created at point B is - 4. 8 k. N • m 148

Absolute Maximum Shear and Moment FR F 2 CL x x' x F 1

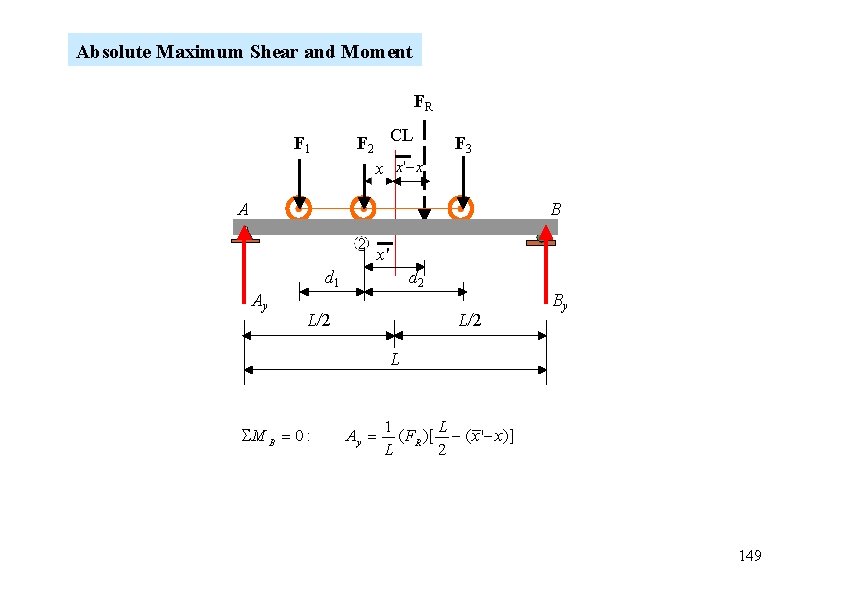
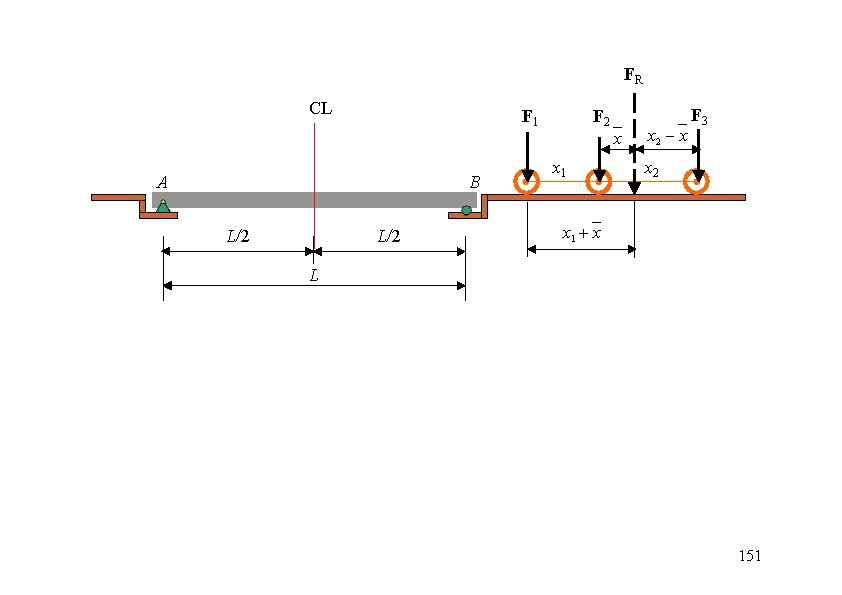
Absolute Maximum Shear and Moment FR F 2 CL x x' x F 1 F 3 A B 2 x' d 1 Ay d 2 L/2 By L M B 0 : Ay 1 L (FR )[ (x' x)] L 2 149

F 1 d 1 M 2 0 : M 2 A 2 (L/2 -

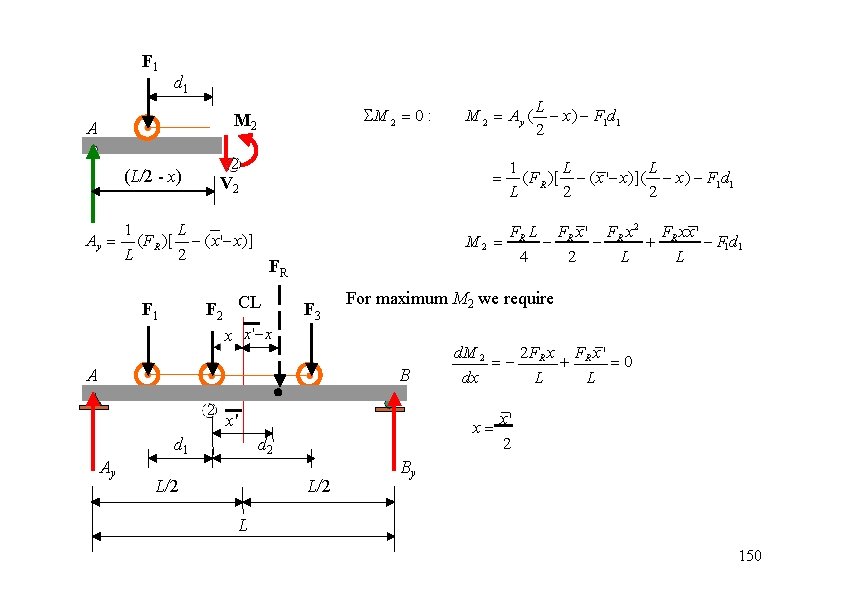
F 1 d 1 M 2 0 : M 2 A 2 (L/2 - x) V 2 1 L Ay (FR )[ (x' x)] L 2 F 3 A For maximum M 2 we require B 2 x' d 1 Ay d. M 2 2 F x F x' R R 0 dx L L x d 2 L/2 1 L L (FR )[ (x' x)]( x) F 1 d 1 L 2 2 FR L FR x' FR x 2 FR xx' M 2 F 1 d 1 4 2 L L FR F 2 CL x x' x F 1 L M 2 Ay ( x) F 1 d 1 2 L/2 x' 2 By L 150

FR CL F 1 A B L/2 F 2 x 1 x x 2

FR CL F 1 A B L/2 F 2 x 1 x x 2 x F 3 x 2 x 1 x L 151

CL FR F 2 b F 1 x 1 A FR x 2 F

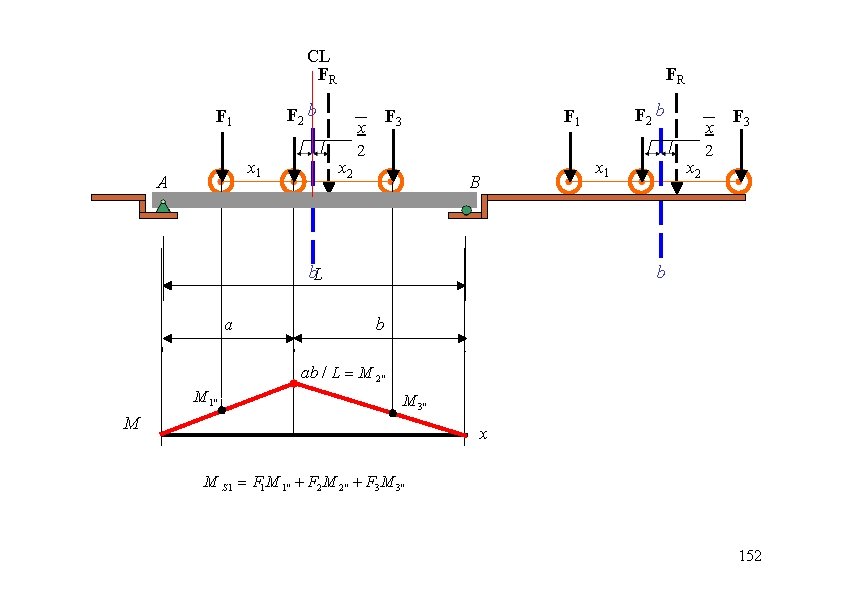
CL FR F 2 b F 1 x 1 A FR x 2 F 3 x 2 B b. L a F 2 b F 1 x 2 x 2 F 3 b b ab / L M 2 '' M 1'' M 3'' M x M S 1 F 1 M 1'' F 2 M 2'' F 3 M 3'' 152

CL FR F 1 A a F 3 F 2 x 1 x 2

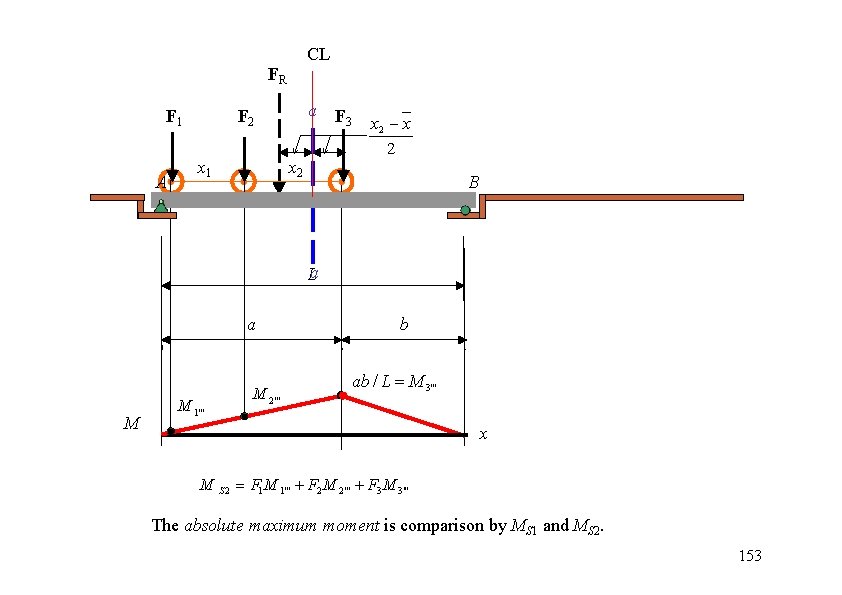
CL FR F 1 A a F 3 F 2 x 1 x 2 B La a M M 1''' M 2''' b ab / L M 3''' x M S 2 F 1 M 1''' F 2 M 2''' F 3 M 3''' The absolute maximum moment is comparison by MS 1 and MS 2. 153

Example 6 -11 Determine the absolute maximum moment on the simply supported beam cased

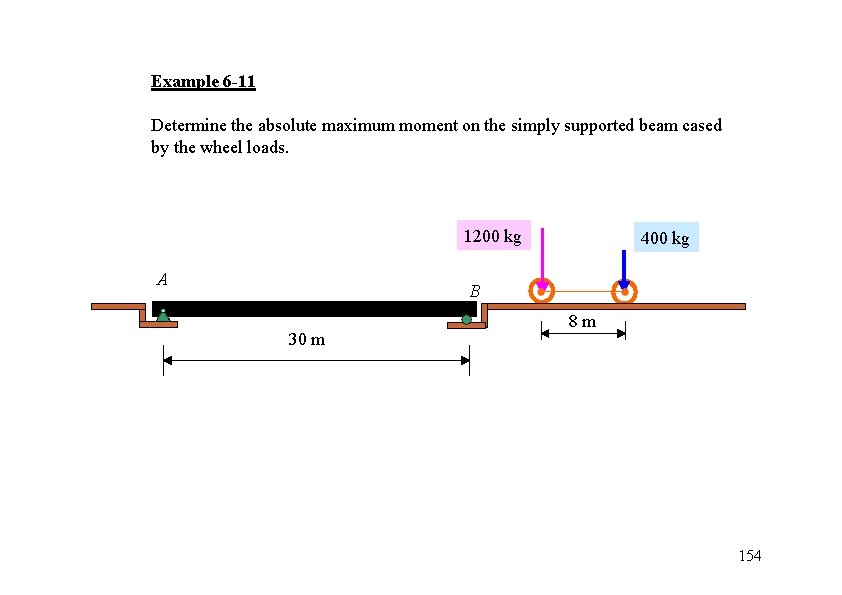
Example 6 -11 Determine the absolute maximum moment on the simply supported beam cased by the wheel loads. 1200 kg A 400 kg B 30 m 8 m 154

1600 kg CL b 1200 kg 3 m A 3 m 400 kg B

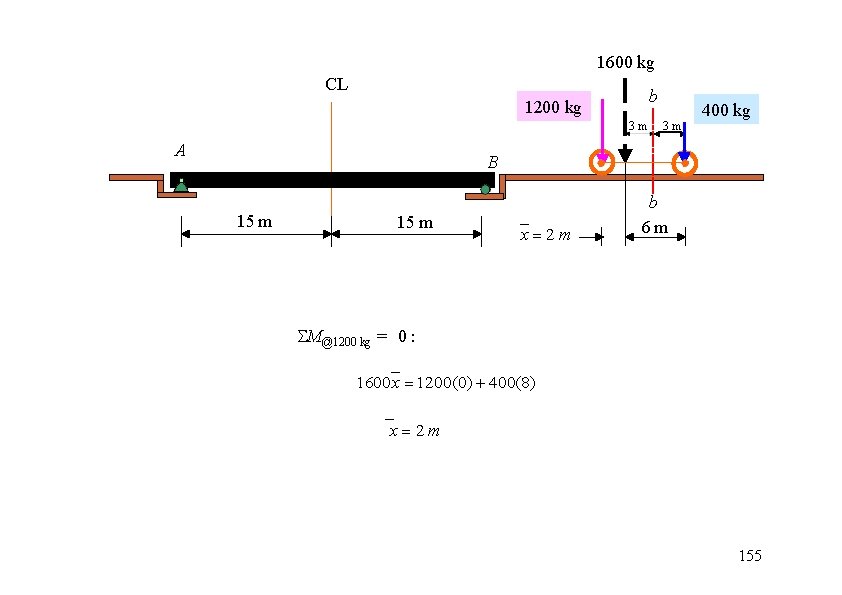
1600 kg CL b 1200 kg 3 m A 3 m 400 kg B 15 m x 2 m b 6 m M@1200 kg = 0 : 1600 x 1200(0) 400(8) x 2 m 155

CL a 1600 kg 1200 kg 1 m 400 kg 1 m A B

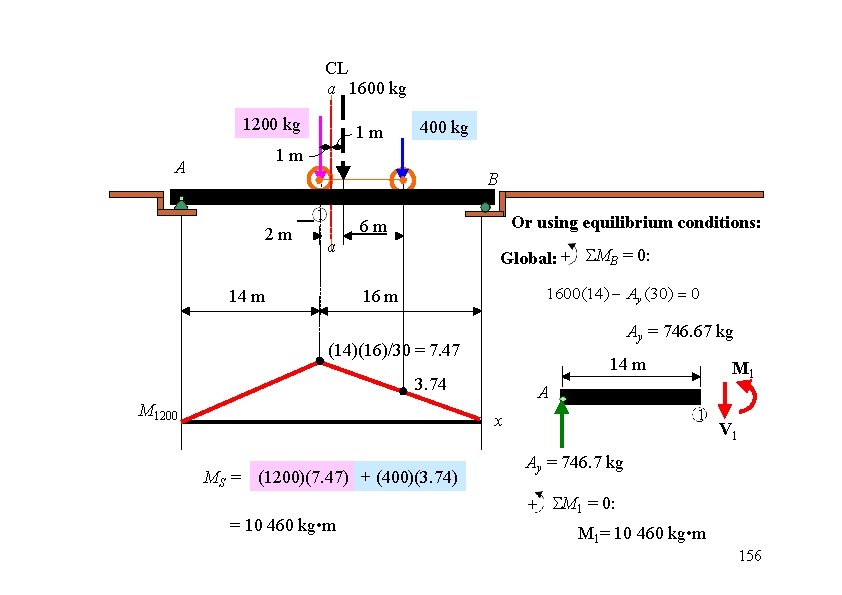
CL a 1600 kg 1200 kg 1 m 400 kg 1 m A B 1 2 m a 14 m Or using equilibrium conditions: 6 m Global: + MB = 0: 1600(14) Ay (30) 0 16 m Ay = 746. 67 kg (14)(16)/30 = 7. 47 14 m 3. 74 M 1200 A 1 x MS = (1200)(7. 47) + (400)(3. 74) = 10 460 kg • m M 1 V 1 Ay = 746. 7 kg + M 1 = 0: M 1= 10 460 kg • m 156

CL 1600 kg b 1200 kg 3 m 400 kg 3 m A B

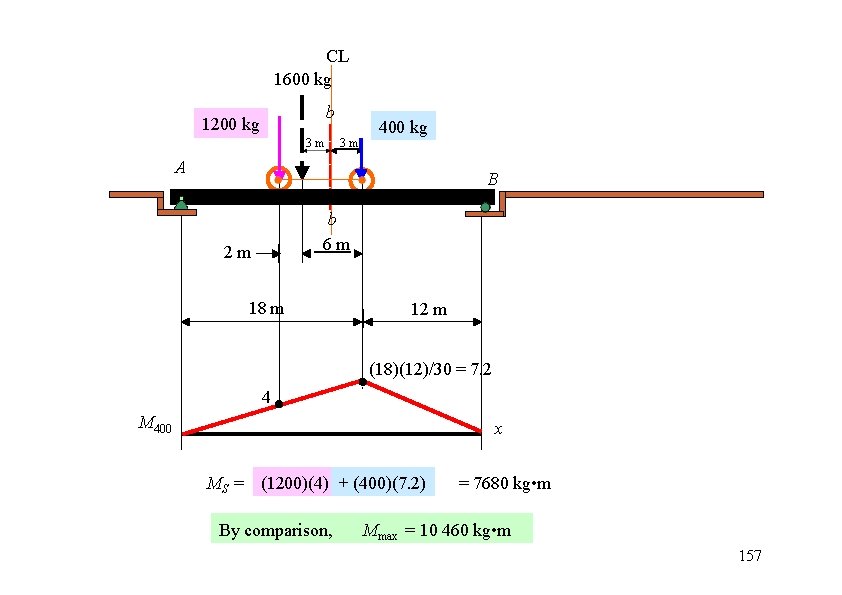
CL 1600 kg b 1200 kg 3 m 400 kg 3 m A B b 6 m 2 m 18 m 12 m (18)(12)/30 = 7. 2 4 M 400 x MS = (1200)(4) + (400)(7. 2) By comparison, = 7680 kg • m Mmax = 10 460 kg • m 157

Example 6 -12 Determine the absolute maximum moment and maximum shear on the simply

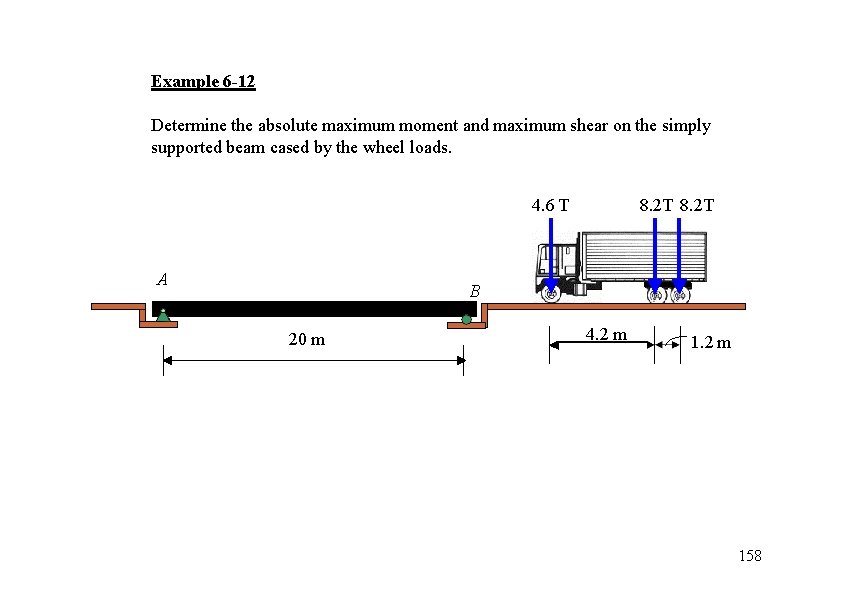
Example 6 -12 Determine the absolute maximum moment and maximum shear on the simply supported beam cased by the wheel loads. 4. 6 T A 8. 2 T B 20 m 4. 2 m 158

FR=21 T Absolute maximum moment 4. 6 T A 8. 2 T B 4.

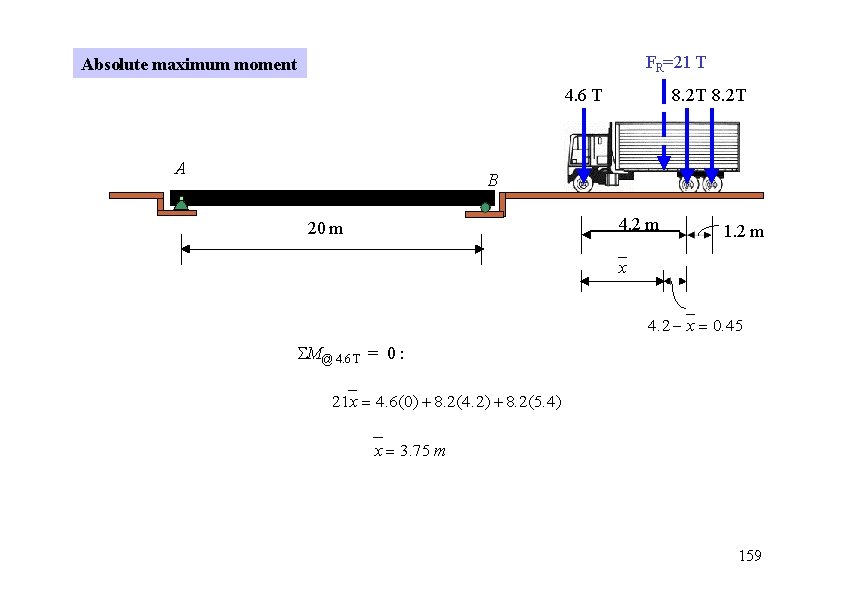
FR=21 T Absolute maximum moment 4. 6 T A 8. 2 T B 4. 2 m 20 m 1. 2 m x 4. 2 x 0. 45 M@ 4. 6 T = 0 : 21 x 4. 6(0) 8. 2(4. 2) 8. 2(5. 4) x 3. 75 m 159

CL FR=21 T 4. 6 T 8. 2 T A B 4. 2 m

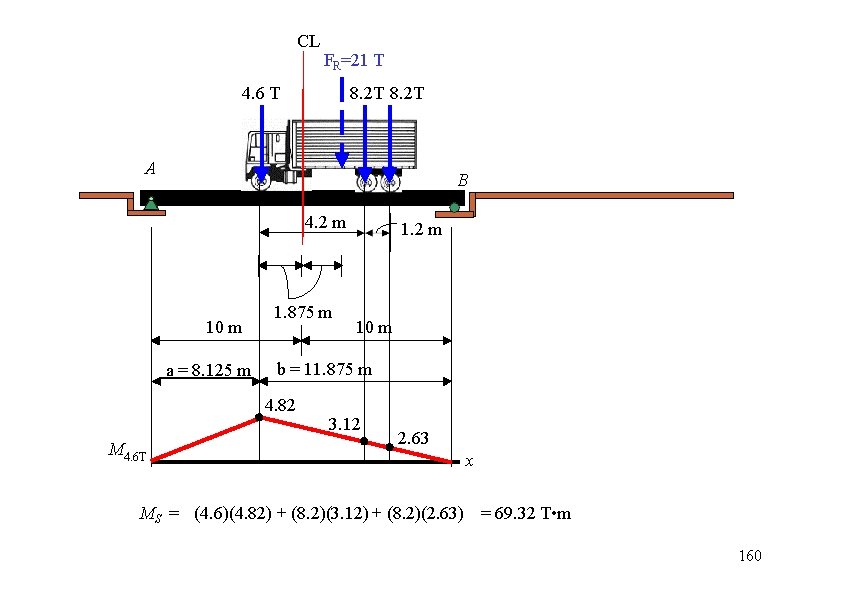
CL FR=21 T 4. 6 T 8. 2 T A B 4. 2 m 10 m a = 8. 125 m 1. 875 m 10 m b = 11. 875 m 4. 82 M 4. 6 T 1. 2 m 3. 12 2. 63 x MS = (4. 6)(4. 82) + (8. 2)(3. 12) + (8. 2)(2. 63) = 69. 32 T • m 160

4. 6 T FR=21 T CL 8. 2 T A B 2 4. 2

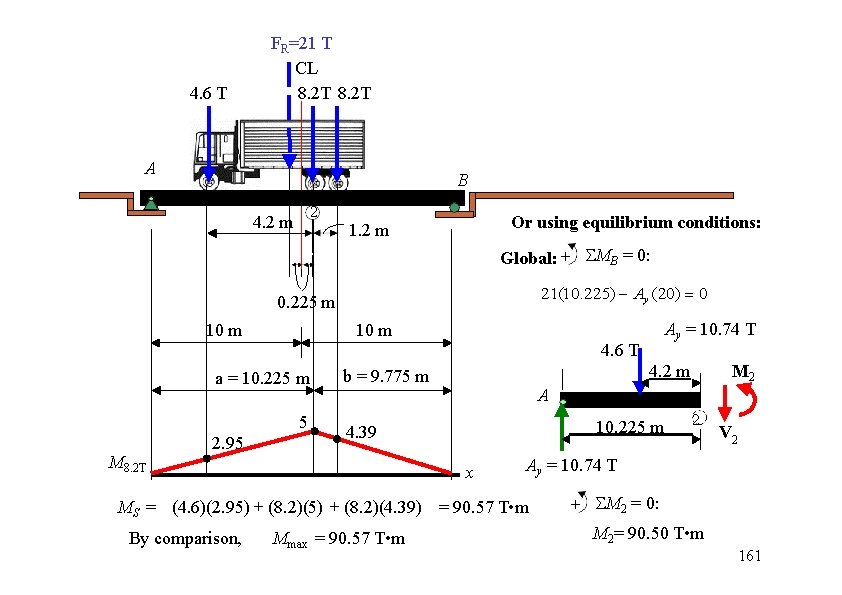
4. 6 T FR=21 T CL 8. 2 T A B 2 4. 2 m Or using equilibrium conditions: 1. 2 m Global: + MB = 0: 21(10. 225) Ay (20) 0 0. 225 m 10 m Ay = 10. 74 T 10 m 4. 6 T a = 10. 225 m 5 M 8. 2 T 2. 95 4. 2 m b = 9. 775 m A 10. 225 m 4. 39 x Mmax = 90. 57 T • m 2 V 2 Ay = 10. 74 T MS = (4. 6)(2. 95) + (8. 2)(4. 39) = 90. 57 T • m By comparison, M 2 + M 2 = 0: M 2= 90. 50 T • m 161

Absolute maximum shear 4. 6 T 8. 2 T 4. 2 m A B

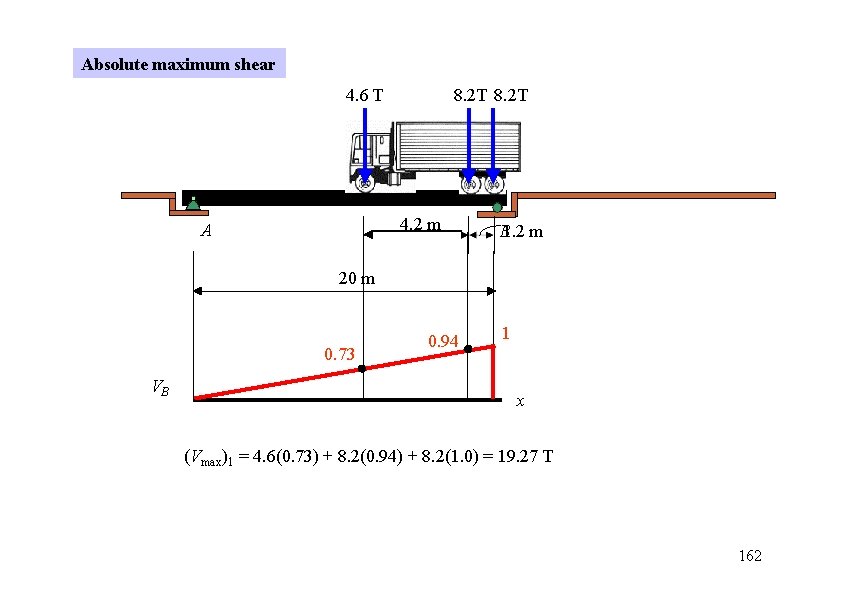
Absolute maximum shear 4. 6 T 8. 2 T 4. 2 m A B 1. 2 m 20 m 0. 73 VB 0. 94 1 x (Vmax)1 = 4. 6(0. 73) + 8. 2(0. 94) + 8. 2(1. 0) = 19. 27 T 162

4. 6 T A 8. 2 T 4. 2 m 1. 2 m B

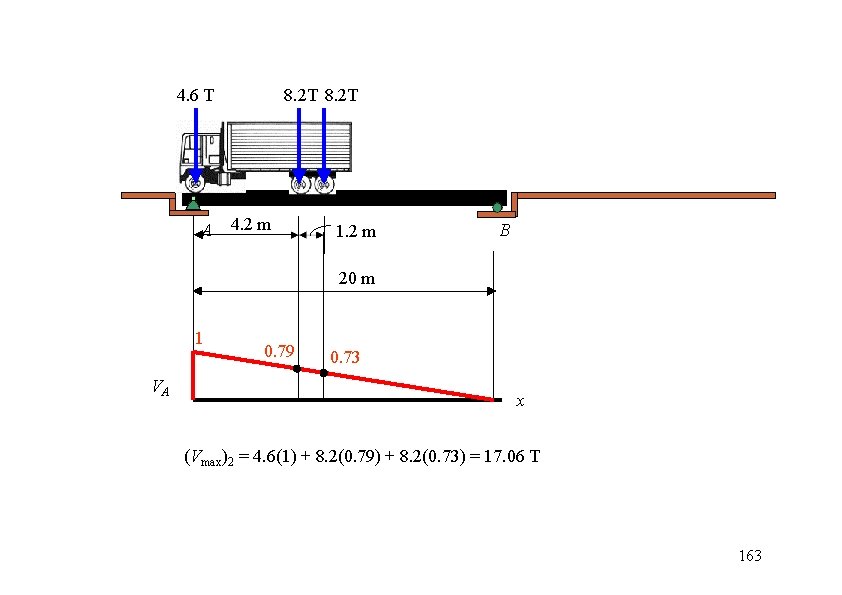
4. 6 T A 8. 2 T 4. 2 m 1. 2 m B 20 m 1 VA 0. 79 0. 73 x (Vmax)2 = 4. 6(1) + 8. 2(0. 79) + 8. 2(0. 73) = 17. 06 T 163

4. 6 T 8. 2 T 4. 2 m A B 1. 2 m

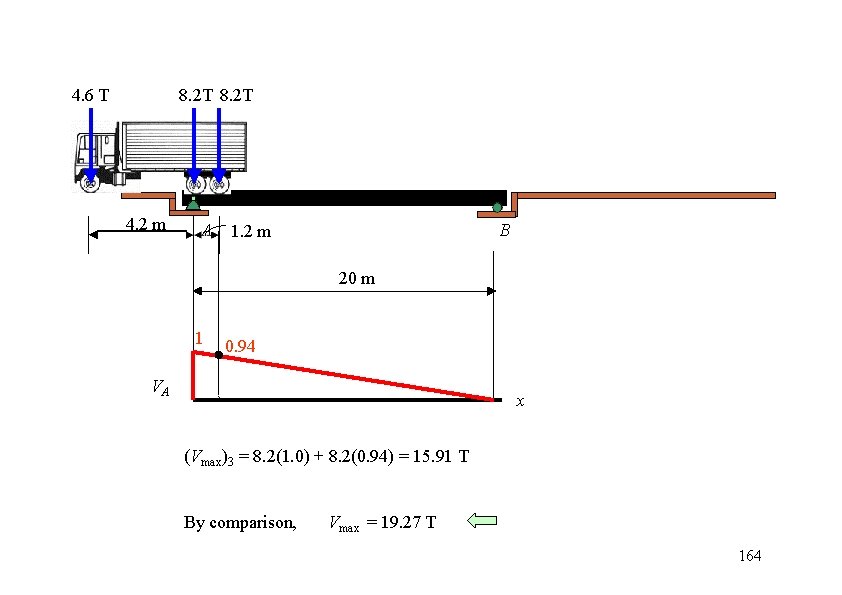
4. 6 T 8. 2 T 4. 2 m A B 1. 2 m 20 m 1 0. 94 VA x (Vmax)3 = 8. 2(1. 0) + 8. 2(0. 94) = 15. 91 T By comparison, Vmax = 19. 27 T 164

Example 6 -13 Determine the absolute maximum moment on the simply supported beam cased

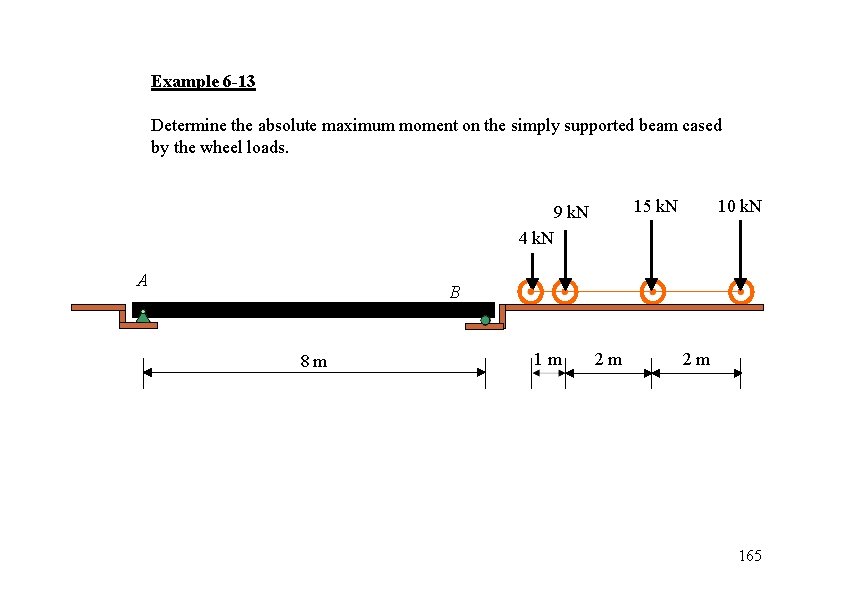
Example 6 -13 Determine the absolute maximum moment on the simply supported beam cased by the wheel loads. 15 k. N 9 k. N 10 k. N 4 k. N A B 8 m 1 m 2 m 2 m 165

SOLUTION FR=38 k. N 15 k. N 9 k. N 4 k. N A

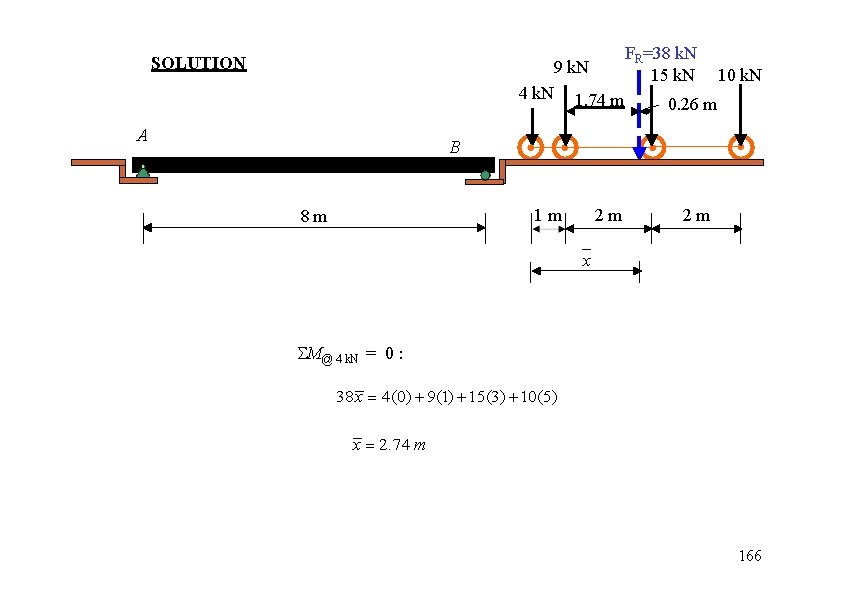
SOLUTION FR=38 k. N 15 k. N 9 k. N 4 k. N A 1. 74 m 10 k. N 0. 26 m B 1 m 8 m 2 m 2 m x M@ 4 k. N = 0 : 38 x 4(0) 9(1) 15(3) 10(5) x 2. 74 m 166

CL 9 k. N 4 k. N FR=38 k. N 15 k. N 10

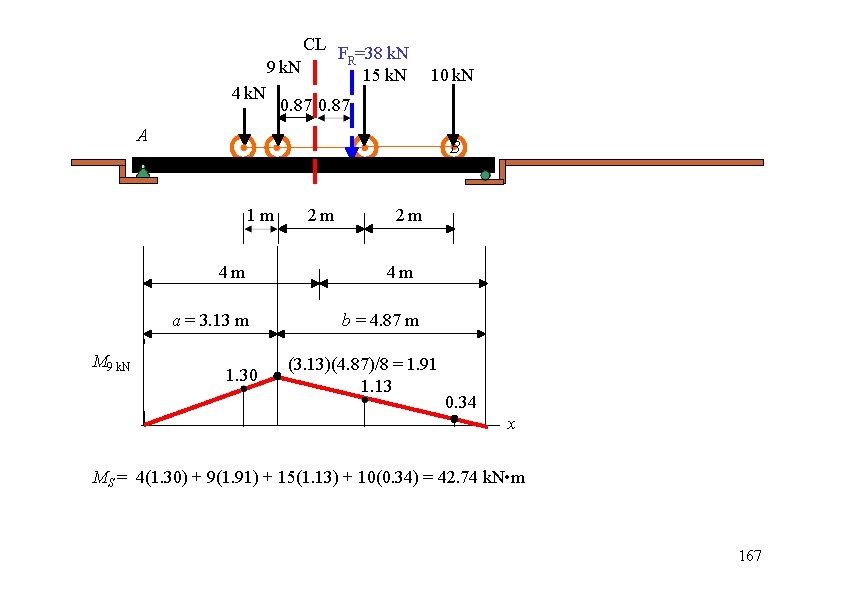
CL 9 k. N 4 k. N FR=38 k. N 15 k. N 10 k. N 0. 87 A B 1 m 4 m a = 3. 13 m M 9 k. N 1. 30 2 m 2 m 4 m b = 4. 87 m (3. 13)(4. 87)/8 = 1. 91 1. 13 0. 34 x MS = 4(1. 30) + 9(1. 91) + 15(1. 13) + 10(0. 34) = 42. 74 k. N • m 167

CL 9 k. N FR 15 k. N 10 k. N 0. 13 m

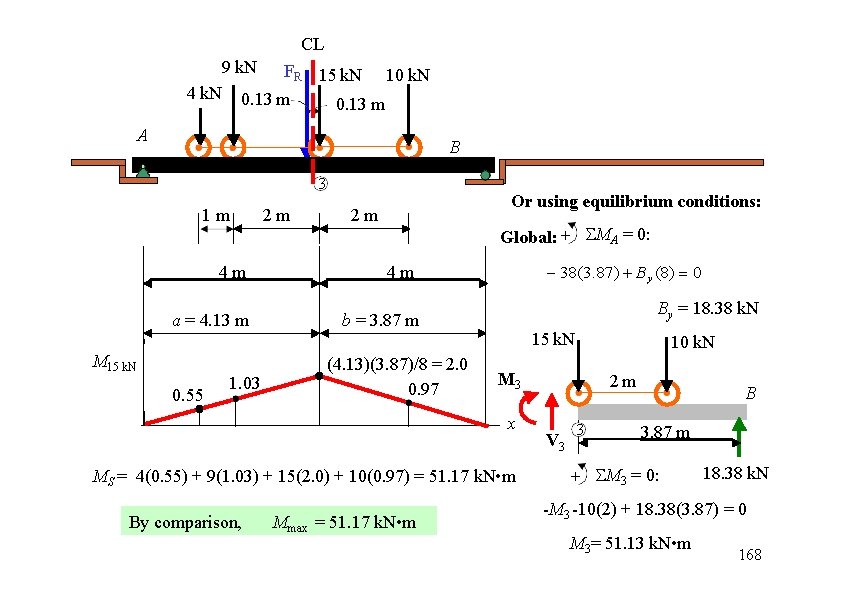
CL 9 k. N FR 15 k. N 10 k. N 0. 13 m 4 k. N A B 3 1 m 4 m a = 4. 13 m M 15 k. N 0. 55 1. 03 2 m Or using equilibrium conditions: 2 m Global: + MA = 0: 38(3. 87) B y (8) 0 4 m By = 18. 38 k. N b = 3. 87 m (4. 13)(3. 87)/8 = 2. 0 0. 97 15 k. N M 3 x MS = 4(0. 55) + 9(1. 03) + 15(2. 0) + 10(0. 97) = 51. 17 k. N • m By comparison, Mmax = 51. 17 k. N • m 10 k. N 2 m V 3 3 B 3. 87 m + M 3 = 0: 18. 38 k. N -M 3 -10(2) + 18. 38(3. 87) = 0 M 3= 51. 13 k. N • m 168