EXAMPLE 5 Standardized Test Practice Use the result

EXAMPLE 1 List possible rational zeros List the possible rational zeros of f using

EXAMPLE 1 b. List possible rational zeros f (x) = 4 x 4 –

Find zeros when the leading coefficient is 1 EXAMPLE 2 Find all real zeros

Find zeros when the leading coefficient is 1 EXAMPLE 2 STEP 2 Test these

EXAMPLE 2 Find zeros when the leading coefficient is 1 Because – 1 is

EXAMPLE 1 Find the number of solutions or zeros a. How many solutions does

EXAMPLE 1 Find the number of solutions or zeros b. How many zeros does

EXAMPLE 2 Find the zeros of a polynomial function Find all zeros of f

EXAMPLE 2 STEP 3 Find the zeros of a polynomial function Find the complex

EXAMPLE 4 Use Descartes’ rule of signs Determine the possible numbers of positive real

EXAMPLE 4 Use Descartes’ rule of signs The coefficients in f (– x) have

EXAMPLE 5 Approximate real zeros Approximate the real zeros of f (x) = x

EXAMPLE 6 Approximate real zeros of a polynomial model TACHOMETER A tachometer measures the

EXAMPLE 6 Approximate real zeros of a polynomial model SOLUTION Substitute 15 for s(x)

Slides: 15

Download presentation

EXAMPLE 5 Standardized Test Practice Use the result to write f (x) as a product of two factors. Then factor completely. f (x) = x 3 – 2 x 2 – 23 x + 60 = (x – 3)(x 2 + x – 20) = (x – 3)(x + 5)(x – 4) The zeros are 3, – 5, and 4. ANSWER The correct answer is A.

EXAMPLE 1 List possible rational zeros List the possible rational zeros of f using the rational zero theorem. a. f (x) = x 3 + 2 x 2 – 11 x + 12 Factors of the constant term: + 1, + 2, + 3, + 4, + 6, + 12 Factors of the leading coefficient: + 1 Possible rational zeros: + 1 , + 2 , + 3 , + 4 , + 6 , + 12 1 1 1 Simplified list of possible zeros: + 1, + 2, + 3, + 4, + 6, + 12

EXAMPLE 1 b. List possible rational zeros f (x) = 4 x 4 – x 3 – 3 x 2 + 9 x – 10 Factors of the constant term: + 1, + 2, + 5, + 10 Factors of the leading coefficient: + 1, + 2, + 4 Possible rational zeros: + 1 , + 2 , + 5 , + 10 , + 1 , + 2 , + 5 4 2 2 4 1 1 + 10 4 Simplified list of possible zeros: + 1, + 2, + 5, + 10, + 1 2 + 5 , + 1 , + 5 2 4 4

Find zeros when the leading coefficient is 1 EXAMPLE 2 Find all real zeros of f (x) = x 3 – 8 x 2 +11 x + 20. SOLUTION STEP 1 List the possible rational zeros. The leading coefficient is 1 and the constant term is 20. So, the possible rational zeros are: x = + 1 , + 2 , + 4 , + 5 , + 10 , + 20 1 1 1

Find zeros when the leading coefficient is 1 EXAMPLE 2 STEP 2 Test these zeros using synthetic division. Test x =1: 1 1 – 8 11 1 – 7 4 1 Test x = – 1: – 1 1 – 8 1 – 9 11 20 4 24 ↑ 1 is not a zero. 20 9 20 20 0 ↑ – 1 is a zero

EXAMPLE 2 Find zeros when the leading coefficient is 1 Because – 1 is a zero of f, you can write f (x) = (x + 1)(x 2 – 9 x + 20). STEP 3 Factor the trinomial in f (x) and use the factor theorem. f (x) = (x + 1) (x 2 – 9 x + 20) = (x + 1)(x – 4)(x – 5) ANSWER The zeros of f are – 1, 4, and 5.

EXAMPLE 1 Find the number of solutions or zeros a. How many solutions does the equation x 3 + 5 x 2 + 4 x + 20 = 0 have? SOLUTION Because x 3 + 5 x 2 + 4 x + 20 = 0 is a polynomial equation of degree 3, it has three solutions. (The solutions are – 5, – 2 i, and 2 i. )

EXAMPLE 1 Find the number of solutions or zeros b. How many zeros does the function f (x) = x 4 – 8 x 3 + 18 x 2 – 27 have? SOLUTION Because f (x) = x 4 – 8 x 3 + 18 x 2 – 27 is a polynomial function of degree 4, it has four zeros. (The zeros are – 1, 3, 3, and 3. )

EXAMPLE 2 Find the zeros of a polynomial function Find all zeros of f (x) = x 5 – 4 x 4 + 4 x 3 + 10 x 2 – 13 x – 14. SOLUTION STEP 1 Find the rational zeros of f. Because f is a polynomial function of degree 5, it has 5 zeros. The possible rational zeros are + 1, + 2, + 7, and + 14. Using synthetic division, you can determine that – 1 is a zero repeated twice and 2 is also a zero. STEP 2 Write f (x) in factored form. Dividing f (x) by its known factors x + 1, and x – 2 gives a quotient of x 2 – 4 x + 7. Therefore: f (x) = (x + 1)2(x – 2)(x 2 – 4 x + 7)

EXAMPLE 2 STEP 3 Find the zeros of a polynomial function Find the complex zeros of f. Use the quadratic formula to factor the trinomial into linear factors. f(x) = (x + 1)2(x – 2) x – (2 + i 3 ) x – (2 – i 3 ) ANSWER The zeros of f are – 1, 2, 2 + i 3 , and 2 – i 3.

EXAMPLE 4 Use Descartes’ rule of signs Determine the possible numbers of positive real zeros, negative real zeros, and imaginary zeros for f (x) = x 6 – 2 x 5 + 3 x 4 – 10 x 3 – 6 x 2 – 8 x – 8. SOLUTION f (x) = x 6 – 2 x 5 + 3 x 4 – 10 x 3 – 6 x 2 – 8 x – 8. The coefficients in f (x) have 3 sign changes, so f has 3 or 1 positive real zero(s). f (– x) = (– x)6 – 2(– x)5 + 3(– x)4 – 10(– x)3 – 6(– x)2 – 8(– x) – 8 = x 6 + 2 x 5 + 3 x 4 + 10 x 3 – 6 x 2 + 8 x – 8

EXAMPLE 4 Use Descartes’ rule of signs The coefficients in f (– x) have 3 sign changes, so f has 3 or 1 negative real zero(s). The possible numbers of zeros for f are summarized in the table below.

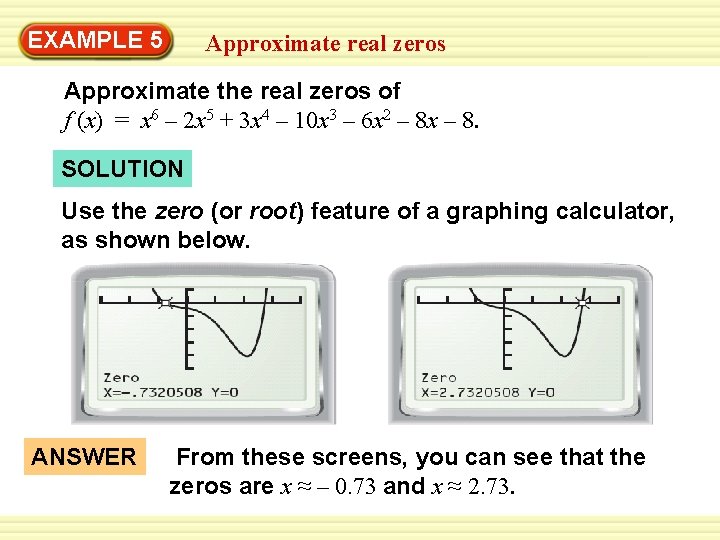
EXAMPLE 5 Approximate real zeros Approximate the real zeros of f (x) = x 6 – 2 x 5 + 3 x 4 – 10 x 3 – 6 x 2 – 8 x – 8. SOLUTION Use the zero (or root) feature of a graphing calculator, as shown below. ANSWER From these screens, you can see that the zeros are x ≈ – 0. 73 and x ≈ 2. 73.

EXAMPLE 6 Approximate real zeros of a polynomial model TACHOMETER A tachometer measures the speed (in revolutions per minute, or RPMs) at which an engine shaft rotates. For a certain boat, the speed x of the engine shaft (in 100 s of RPMs) and the speed s of the boat (in miles per hour) are modeled by s (x) = 0. 00547 x 3 – 0. 225 x 2 + 3. 62 x – 11. 0 What is the tachometer reading when the boat travels 15 miles per hour?

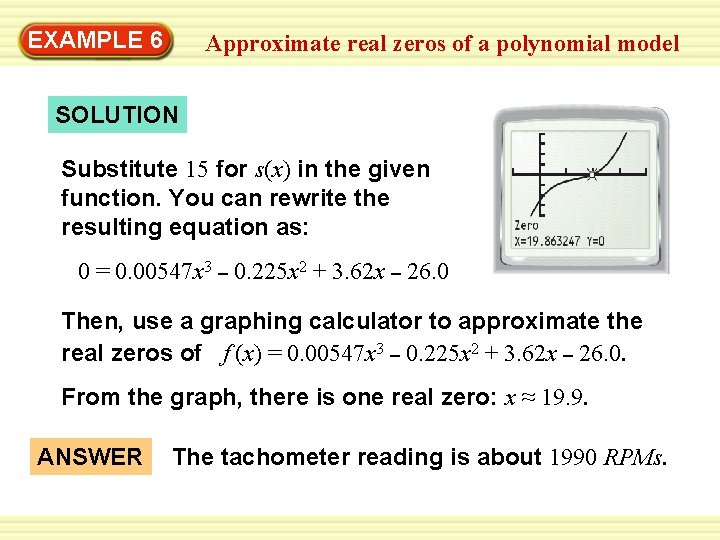
EXAMPLE 6 Approximate real zeros of a polynomial model SOLUTION Substitute 15 for s(x) in the given function. You can rewrite the resulting equation as: 0 = 0. 00547 x 3 – 0. 225 x 2 + 3. 62 x – 26. 0 Then, use a graphing calculator to approximate the real zeros of f (x) = 0. 00547 x 3 – 0. 225 x 2 + 3. 62 x – 26. 0. From the graph, there is one real zero: x ≈ 19. 9. ANSWER The tachometer reading is about 1990 RPMs.