Example 3 Show that the Vertex Cover VC

• Example 3 : Show that the Vertex Cover (VC) Problem is NP-complete. Given 3 SAT problem is NPC, show that VC problem is NPC. 3 SAT Problem Instance : Given a set of variables U = {u 1, u 2, …, un} and a collection of clauses C = {c 1, c 2, …, cm} over U such that | ci | = 3 for 1 i m. Question : Is there a truth assignment for U that satisfies all clauses in C? Note : 3 SAT problem is a restricted problem of SATISFIABILITY problem. Young CS 530 Ad. Algo. D&A NP-Completeness 1

Vertex Cover (VC) Problem Instance : Given an undirected graph G=(V, E) and a positive integer K |V| Question : Is there a vertex cover of size K or less for G, i. e. a subset V’ V such that |V’| K and, for each (u, v) E, at least one of u or v V’. • VC is in NP guess a set of vertices V’ V O(|V|) verify that |V’| K and, for each (u, v) E, u V’ or v V’ O(|V|+|E|) Young CS 530 Ad. Algo. D&A NP-Completeness 2

• 3 SAT VC Given arbitrary instance of 3 SAT, i. e. U = {u 1, u 2, …, un} and C = {c 1, c 2, …, cm}. Construct an instance of VC as follows : § G = (V , E ) and K = n+2 m § V = Vu Vc Vu = {u 1 t, u 1 f, u 2 t, u 2 f, …, unt, unf} and Vc = {a 11, a 12, a 13} {a 21, a 22, a 23} … {am 1, am 2, am 3} Young CS 530 Ad. Algo. D&A NP-Completeness 3

§ E = Eu Ec Euc Eu = {(u 1 t, u 1 f) , (u 2 t, u 2 f) , …, (unt, unf)} Ec = {(a 11, a 12) , (a 12, a 13), (a 13, a 11)} … {(am 1, am 2) , (am 2, am 3), (am 3, am 1)} Assume ci = (xi, yi, zi) for 1 i m, find the corresponding vertices, xi, yi, zi, in Vu Euc = {(x 1, a 11), (y 1, a 12), (z 1, a 13)} … {(xm, am 1), (ym, am 2), (zm, am 3)} Young CS 530 Ad. Algo. D&A NP-Completeness 4

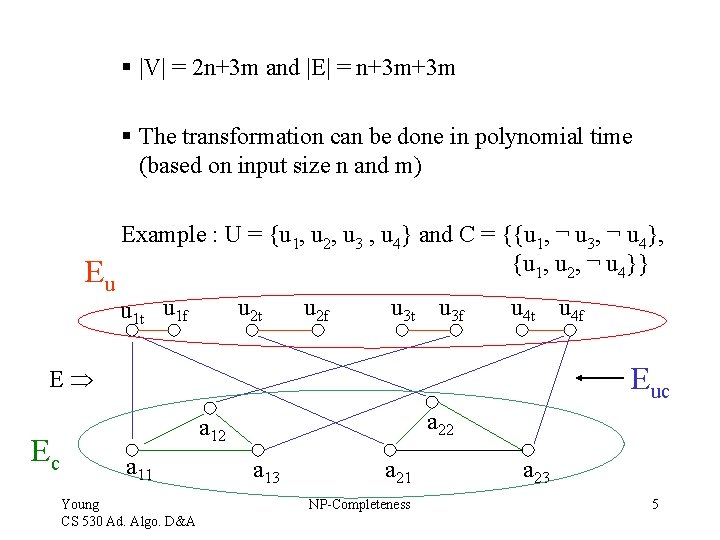
§ |V| = 2 n+3 m and |E| = n+3 m+3 m § The transformation can be done in polynomial time (based on input size n and m) Eu Example : U = {u 1, u 2, u 3 , u 4} and C = {{u 1, ¬ u 3, ¬ u 4}, {u 1, u 2, ¬ u 4}} u 1 t u 1 f u 2 t u 2 f u 3 t u 3 f u 4 t u 4 f Euc E Ec a 22 a 11 Young CS 530 Ad. Algo. D&A a 13 a 21 NP-Completeness a 23 5

Major Property : if there is a vertex cover set V’ K = n+2 m, then a) |V’| = n+ 2 m, and b) V’ must include exactly 1 vertex in {uit, uif} for 1 i n from Vu and at exactly 2 vertices in {ai 1, ai 2, ai 3} for 1 i m from Vc, i. e. n vertices from Vu and 2 m vertices from Vc ® Look at edges in Eu and Ec, a vertex cover set V’ must include at least 1 vertex {uit, uif} for 1 i n, and at least 2 vertices from {ai 1, ai 2, ai 3} for 1 i m. Since |V’| K |V’| = K Young CS 530 Ad. Algo. D&A NP-Completeness 6

To show the transformation is correct : The 3 SAT problem has a solution if and only if the VC problem has a solution. Ø If VC problem has a solution then 3 SAT problem has a solution From the above property, V’ contains n vertices from Vu and 2 m vertices from Vc From Vu , the truth assignment for {u 1, u 2, …, un} in 3 SAT is ui = T if uit V’ ui = F if uif V’ for 1 i n Young CS 530 Ad. Algo. D&A NP-Completeness 7

To see that this is a solution for 3 SAT : we must show that for each ci = (xi, yi, zi), there is at least one variable i {xi, yi, zi} which set ci to TRUE, 1 i n From the above property, exactly 2 vertices from {ai 1, ai 2, ai 3} in V’, for 1 i m only cover 2 edges from {(xi, ai 1), (yi, ai 2), (zi, ai 3)} from Euc assume the edge (xi, ai 1) is not covered by 2 vertices from {ai 1, ai 2, ci 3} then xi V’ since V’ is a vertex cover set xi set the clause ci to True for 1 i n Young CS 530 Ad. Algo. D&A NP-Completeness 8

Ø If the 3 SAT problem has a solution, then the VC problem has a solution The vertex cover set V’ with exactly n+2 m vertices can be obtained as follows : From the truth assignment for {u 1, u 2, …, un} in 3 SAT, we get n vertices from Vu, i. e. uit V’ if ui = T; otherwise uif V’ for 1 i n This covers all edges in Eu and at least one edge in {(xi, ai 1), (yi, ai 2), (zi, ai 3)} for 1 i m From Vc, include 2 vertices from each {ai 1, ai 2, ai 3} into V’, for 1 i m. These 2 vertices cover all edges {(ai 1, ai 2) , (ai 2, ai 3), (ai 3, ai 1)} and also cover edges in Euc that are not covered previously. Young CS 530 Ad. Algo. D&A NP-Completeness 9