EXAMPLE 2 Find the scale factor Determine whether

EXAMPLE 2 Find the scale factor SOLUTION STEP 1 Identify pairs of congruent angles.

EXAMPLE 2 Find the scale factor SOLUTION STEP 2 Show that corresponding side lengths

EXAMPLE 2 Find the scale factor SOLUTION The ratios are equal, so the corresponding

EXAMPLE 3 Use similar polygons ALGEBRA In the diagram, ∆DEF ~ ∆MNP. Find the

EXAMPLE 3 Use similar polygons SOLUTION The triangles are similar, so the corresponding side

GUIDED PRACTICE for Examples 2 and 3 In the diagram, ABCD ~ QRST. 2.

GUIDED PRACTICE for Examples 2 and 3 STEP 2 Show that corresponding side lengths

GUIDED PRACTICE for Examples 2 and 3 The ratios are equal, so the corresponding

GUIDED PRACTICE for Examples 2 and 3 In the diagram, ABCD ~ QRST. 3.

GUIDED PRACTICE ANSWER So the value of x is 8 for Examples 2 and

Slides: 11

Download presentation

EXAMPLE 2 Find the scale factor Determine whether the polygons are similar. If they are, write a similarity statement and find the scale factor of ZYXW to FGHJ.

EXAMPLE 2 Find the scale factor SOLUTION STEP 1 Identify pairs of congruent angles. From the diagram, you can see that Z F, Y G, and X H. Angles W and J are right angels, so W J. So, the corresponding angles are congruent.

EXAMPLE 2 Find the scale factor SOLUTION STEP 2 Show that corresponding side lengths are proportional. ZY = FG 25 20 XW = HJ 15 12 = 5 4 YX = GH 30 24 = 5 4 WZ = JF 5 20 = 4 16 = 5 4

EXAMPLE 2 Find the scale factor SOLUTION The ratios are equal, so the corresponding side lengths are proportional. ANSWER So ZYXW ~ FGHJ. The scale factor of ZYXW to FGHJ is 5. 4

EXAMPLE 3 Use similar polygons ALGEBRA In the diagram, ∆DEF ~ ∆MNP. Find the value of x.

EXAMPLE 3 Use similar polygons SOLUTION The triangles are similar, so the corresponding side lengths are proportional. MN = NP EF DE 12 = 20 x 9 12 x = 180 x = 15 Write proportion. Substitute. Cross Products Property Solve for x.

GUIDED PRACTICE for Examples 2 and 3 In the diagram, ABCD ~ QRST. 2. What is the scale factor of QRST to ABCD ? SOLUTION STEP 1 Identify pairs of congruent angles. From the diagram, you can see that A = Q, T = D, and B = R. Angles C and S are right angles. So, all the corresponding angles are congruent.

GUIDED PRACTICE for Examples 2 and 3 STEP 2 Show that corresponding side lengths are proportional. QT = AD 5 10 QR = AB 6 12 = 1 2 TS = DC 8 16 = 1 2 RS = BC 4 x = 1 2

GUIDED PRACTICE for Examples 2 and 3 The ratios are equal, so the corresponding side lengths are proportional. ANSWER So QRST ~ ABCD. The scale factor of QRST to ABCD 1. 2

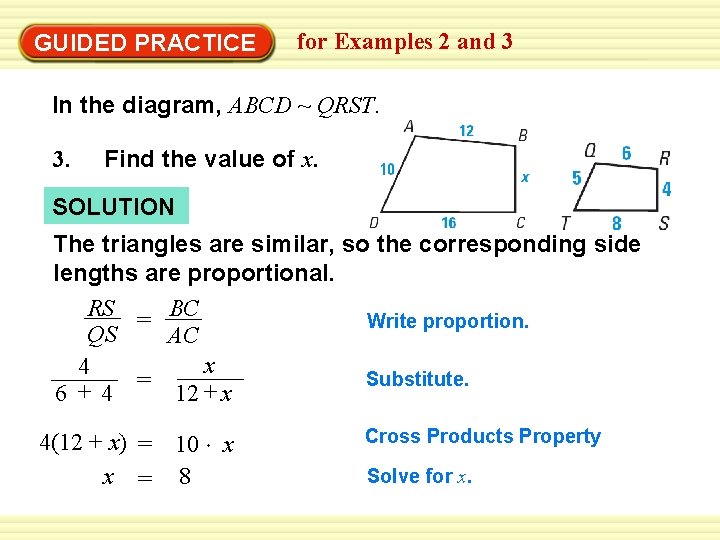
GUIDED PRACTICE for Examples 2 and 3 In the diagram, ABCD ~ QRST. 3. Find the value of x. SOLUTION The triangles are similar, so the corresponding side lengths are proportional. RS Write proportion. = BC QS AC x 4 Substitute. = + 12 x 6 +4 4(12 + x) = 10 x x = 8 Cross Products Property Solve for x.

GUIDED PRACTICE ANSWER So the value of x is 8 for Examples 2 and 3