Example 1 The continuous random variable X has

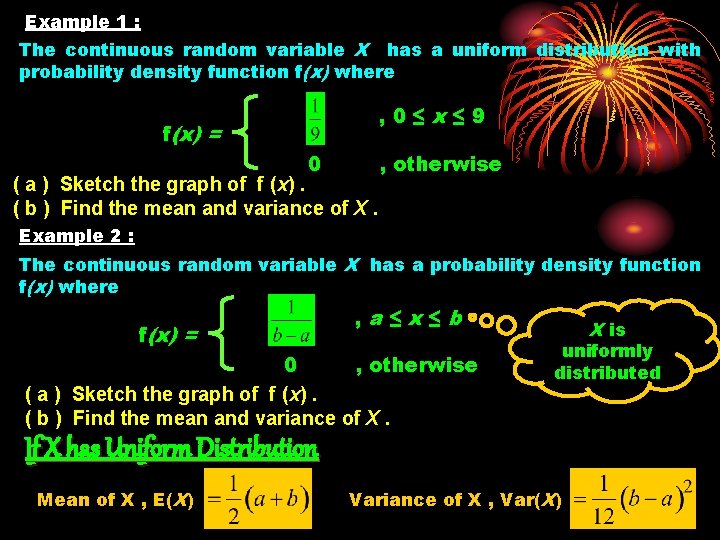
Example 1 : The continuous random variable X has a uniform distribution with probability density function f(x) where , 0≤x≤ 9 f(x) = 0 ( a ) Sketch the graph of f (x). ( b ) Find the mean and variance of X. , otherwise Example 2 : The continuous random variable X has a probability density function f(x) where f(x) = , a≤x≤b 0 , otherwise ( a ) Sketch the graph of f (x). ( b ) Find the mean and variance of X. uniformly distributed If X has Uniform Distribution Mean of X , E(X) X is Variance of X , Var(X)

Example 3 : The continuous random variable X has a uniform distribution in the interval [ -3 , 3 ]. Find (a) P(-4< X ≤ -1) ( b ) P ( X > 2. 2 ) ( c ) mean and standard deviation of X. Ex 8. 5 pg. 384 Q. 13 – 18 Example 4 : The continuous random variable X has a probability density function f(x) where f(x) = 2 e-2 x , x≥ 0 0 otherwise , Find ( a ) P ( X ≤ 0. 1 ) ( b ) P ( X > 0. 05 ) ( c ) mean and variance of X.

Example 5 : The continuous random variable X has a negative exponential distribution with the probability density function f(x) where f(x) = where e- x , x≥ 0 0 otherwise Ex 8. 5 pg. 384 , is a positive constant. Determine the mean and variance of X. Q. 19 – 21 If X has Negative Exponential Distribution Mean of X , E(X) Variance of X , Var(X) Example 6 : The lifespan of a light bulb follows a negative distribution with a mean lifespan of 500 hours. exponential (a) Find the probability that the bulb functions after 600 hours. (b) Given that the bulb still functions after 600 hours , find the probability that the bulb will function after 700 hours. (c) Find the standard deviation of the lifespan of these light bulbs.