EXAMPLE 1 Is either Use the SSS Similarity

  • Slides: 11
Download presentation
EXAMPLE 1 Is either Use the SSS Similarity Theorem DEF or GHJ similar to

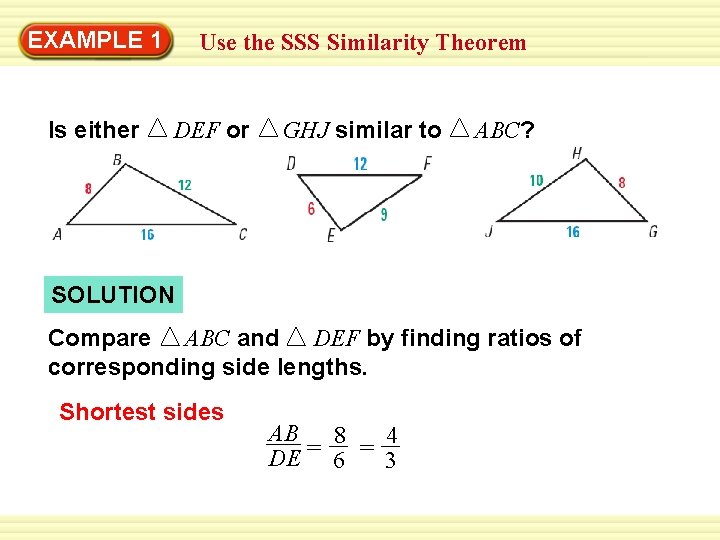
EXAMPLE 1 Is either Use the SSS Similarity Theorem DEF or GHJ similar to ABC? SOLUTION Compare ABC and DEF by finding ratios of corresponding side lengths. Shortest sides AB 8 4 = = DE 6 3

EXAMPLE 1 Use the SSS Similarity Theorem Longest sides Remaining sides CA 16 4

EXAMPLE 1 Use the SSS Similarity Theorem Longest sides Remaining sides CA 16 4 = = 3 FD 12 4 BC 12 = = 3 EF 9 ANSWER All of the ratios are equal, so Compare ABC and GHJ by finding ratios of corresponding side lengths. Shortest sides AB 8 1 GH = 8 = ABC ~ DEF.

EXAMPLE 1 Use the SSS Similarity Theorem Longest sides CA 16 1 JG =

EXAMPLE 1 Use the SSS Similarity Theorem Longest sides CA 16 1 JG = 16 = Remaining sides BC = 12 = 6 HJ 10 5 ANSWER The ratios are not all equal, so not similar. ABC and GHJ are

EXAMPLE 2 Use the SSS Similarity Theorem ALGEBRA Find the value of x that

EXAMPLE 2 Use the SSS Similarity Theorem ALGEBRA Find the value of x that makes ABC ~ DEF. SOLUTION STEP 1 Find the value of x that makes corresponding side lengths proportional. 4 x – 1 = 12 18 Write proportion.

EXAMPLE 2 Use the SSS Similarity Theorem 4 18 = 12(x – 1) 72

EXAMPLE 2 Use the SSS Similarity Theorem 4 18 = 12(x – 1) 72 = 12 x – 12 7=x Cross Products Property Simplify. Solve for x. STEP 2 Check that the side lengths are proportional when x = 7. BC = x – 1 = 6 AB ? BC DE = EF 6 4 12 = 18

EXAMPLE 2 Use the SSS Similarity Theorem DF = 3(x + 1) = 24

EXAMPLE 2 Use the SSS Similarity Theorem DF = 3(x + 1) = 24 AB ? AC DE = DF 8 4 12 = 24 ANSWER When x = 7, the triangles are similar by the SSS Similarity Theorem.

GUIDED PRACTICE 1. for Examples 1 and 2 Which of the three triangles are

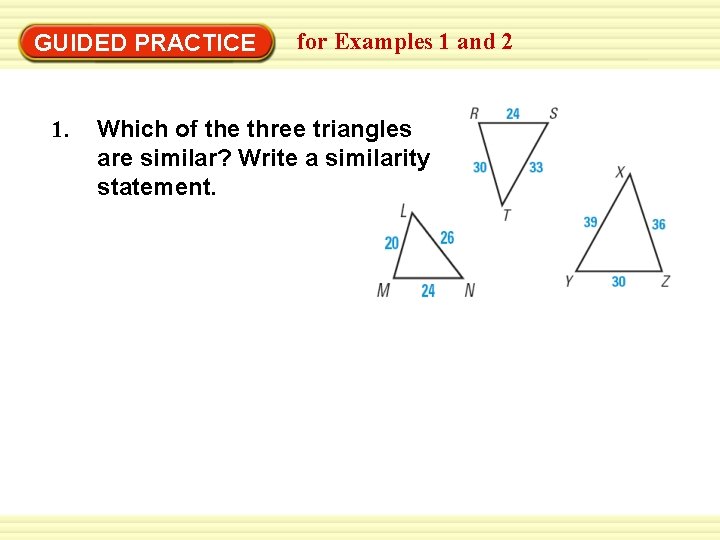
GUIDED PRACTICE 1. for Examples 1 and 2 Which of the three triangles are similar? Write a similarity statement.

GUIDED PRACTICE for Examples 1 and 2 SOLUTION Compare MLN and RST by finding

GUIDED PRACTICE for Examples 1 and 2 SOLUTION Compare MLN and RST by finding ratios of corresponding side lengths. LM 20 5 Shortest sides RS = 24 = 6 Longest sides ST = 33 LN 24 Remaining sides LN = 36 = 13 RT 30 15 The ratios are not all equal, so not similar. LMN and RST are

GUIDED PRACTICE for Examples 1 and 2 Compare LMN and ZYX by finding ratios

GUIDED PRACTICE for Examples 1 and 2 Compare LMN and ZYX by finding ratios of corresponding side lengths. LM 20 2 Shortest sides YZ = 30 = 3 Longest sides LN 26 2 = = XZ 39 3 Remaining sides MN = 24 = 2 XZ 36 3 ANSWER All of the ratios are equal, so MLN ~ ZYX.

GUIDED PRACTICE 2. for Examples 1 and 2 The shortest side of a triangle

GUIDED PRACTICE 2. for Examples 1 and 2 The shortest side of a triangle similar to RST is 12 units long. Find the other side lengths of the triangle. A 12 y x C Find the value of x that makes corresponding side lengths proportional. 24 = 30 x 12 24 x = 12 30 x = 15 B Write proportion. Cross Products Property

GUIDED PRACTICE for Examples 1 and 2 Again to find out y 24 =

GUIDED PRACTICE for Examples 1 and 2 Again to find out y 24 = 33 y 12 24 y = 12 33 Write proportion. Cross Products Property y = 16. 5 ANSWER So x = AC = 15 and y = BC = 16. 5

WarmUp 1 Exercises EXAMPLE Use the SSS SimilarityWarmUp 1 Exercises EXAMPLE Use the SSS Similarity
SIMILARITY THEOREMS Similarity in Triangles AngleAngle Similarity PostulateSIMILARITY THEOREMS Similarity in Triangles AngleAngle Similarity Postulate
Distance Similarity Measures Similarity and Dissimilarity Similarity NumericalDistance Similarity Measures Similarity and Dissimilarity Similarity Numerical
Similarity Proportions Similarity Statements Similarity Ratio 10 10Similarity Proportions Similarity Statements Similarity Ratio 10 10
NLP Text Similarity Morphological Similarity Stemming Morphological SimilarityNLP Text Similarity Morphological Similarity Stemming Morphological Similarity
SIMILARITY THEOREMS Similarity in Triangles AngleAngle Similarity PostulateSIMILARITY THEOREMS Similarity in Triangles AngleAngle Similarity Postulate
SIMILARITY THEOREMS Similarity in Triangles AngleAngle Similarity TheoremSIMILARITY THEOREMS Similarity in Triangles AngleAngle Similarity Theorem
Validation of SMOS SSS with in situ SSSValidation of SMOS SSS with in situ SSS
MSCBMS interaxis in SSS Study on 32 SSSMSCBMS interaxis in SSS Study on 32 SSS
Overall Design of SSS Software Review of SSSOverall Design of SSS Software Review of SSS