EXAMPLE 1 Graph an equation of a circle

  • Slides: 10
Download presentation
EXAMPLE 1 Graph an equation of a circle Graph y 2 = – x

EXAMPLE 1 Graph an equation of a circle Graph y 2 = – x 2 + 36. Identify the radius of the circle. SOLUTION STEP 1 Rewrite the equation y 2 = – x 2 + 36 in standard form as x 2 + y 2 = 36. STEP 2 Identify the center and radius. From the equation, the graph is a circle centered at the origin with radius r = 36 = 6.

EXAMPLE 1 Graph an equation of a circle STEP 3 Draw the circle. First

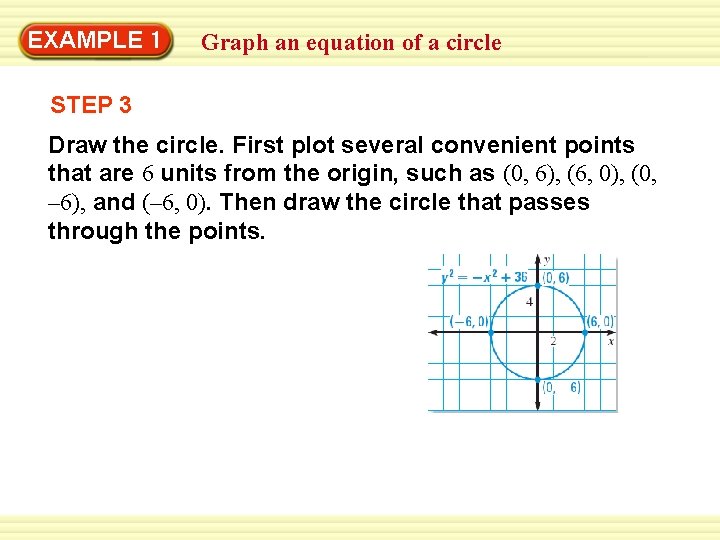
EXAMPLE 1 Graph an equation of a circle STEP 3 Draw the circle. First plot several convenient points that are 6 units from the origin, such as (0, 6), (6, 0), (0, – 6), and (– 6, 0). Then draw the circle that passes through the points.

EXAMPLE 2 Write an equation of a circle The point (2, – 5) lies

EXAMPLE 2 Write an equation of a circle The point (2, – 5) lies on a circle whose center is the origin. Write the standard form of the equation of the circle. SOLUTION Because the point (2, – 5) lies on the circle, the circle’s radius r must be the distance between the center (0, 0) and (2, – 5). Use the distance formula. r = (2 – 0)2 + (– 5 – 0)2 = 4 + 25 = 29 The radius is 29

EXAMPLE 2 Write an equation of a circle Use the standard form with r

EXAMPLE 2 Write an equation of a circle Use the standard form with r = equation of the circle. x 2 + y 2 = r 2 x 2 + y 2 = ( x 2 + y 2 = 29 29 to write an Standard form 29 )2 Substitute Simplify 29 for r

EXAMPLE 3 Standardized Test Practice SOLUTION A line tangent to a circle is perpendicular

EXAMPLE 3 Standardized Test Practice SOLUTION A line tangent to a circle is perpendicular to the radius at the point of tangency. Because the radius to the point (1– 3, 2) has slope 2– 0 2 m – =– 3– 0 = 3

EXAMPLE 3 Standardized Test Practice the slope of the tangent line at (– 3,

EXAMPLE 3 Standardized Test Practice the slope of the tangent line at (– 3, 2) is the negative reciprocal of – 2 or 3 An equation of 2 3 the tangent line is as follows: y – 2 = 3 (x – (– 3)) 2 y – 2 = 3 x + 9 2 2 y = 3 x + 13 2 2 Point-slope form Distributive property Solve for y. ANSWER The correct answer is C.

GUIDED PRACTICE for Examples 1, 2, and 3 Graph the equation. Identify the radius

GUIDED PRACTICE for Examples 1, 2, and 3 Graph the equation. Identify the radius of the circle. 1. x 2 + y 2 = 9 SOLUTION 3

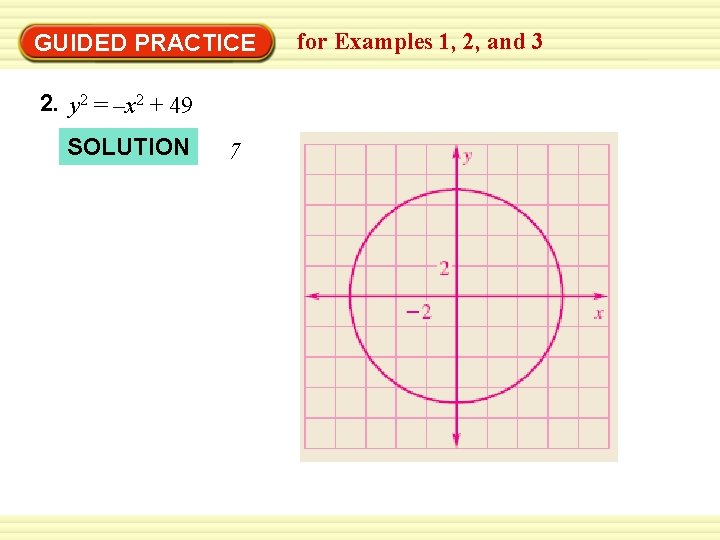
GUIDED PRACTICE 2. y 2 = –x 2 + 49 SOLUTION 7 for Examples

GUIDED PRACTICE 2. y 2 = –x 2 + 49 SOLUTION 7 for Examples 1, 2, and 3

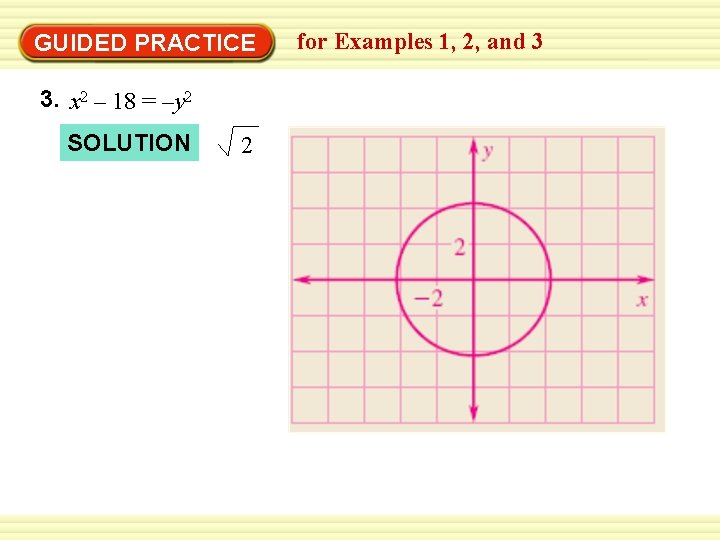
GUIDED PRACTICE 3. x 2 – 18 = –y 2 SOLUTION 2 for Examples

GUIDED PRACTICE 3. x 2 – 18 = –y 2 SOLUTION 2 for Examples 1, 2, and 3

GUIDED PRACTICE for Examples 1, 2, and 3 4. Write the standard form of

GUIDED PRACTICE for Examples 1, 2, and 3 4. Write the standard form of the equation of the circle that passes through (5, – 1) and whose center is the origin. SOLUTION x 2 + y 2 = 26 5. Write an equation of the line tangent to the circle x 2 + y 2 = 37 at (6, 1). SOLUTION y = – 6 x + 37