EXAMPLE 1 Graph a vertical translation Graph y

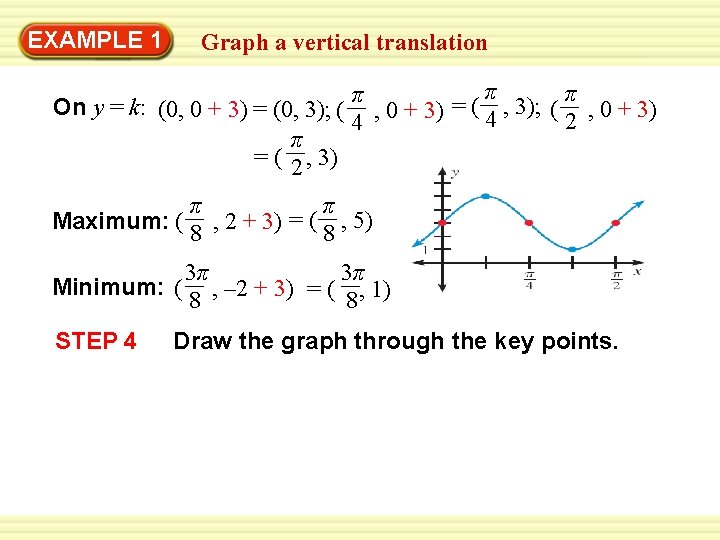
EXAMPLE 1 Graph a vertical translation Graph y = 2 sin 4 x + 3. SOLUTION STEP 1 Identify the amplitude, period, horizontal shift, and vertical shift. Amplitude: a = 2 Horizontal shift: h = 0 π Period: 2 π = b 4 2 Vertical shift: k = 3 STEP 2 Draw the midline of the graph, y = 3. STEP 3 Find the five key points.

EXAMPLE 1 Graph a vertical translation π π π On y = k: (0, 0 + 3) = (0, 3); ( , 0 + 3) = ( 4 , 3); ( , 0 + 3) 2 4 π = ( 2 , 3) π π = ( , 5) Maximum: ( 8 , 2 + 3) 8 3π 3π Minimum: ( , – 2 + 3) = ( , 1) 8 8 STEP 4 Draw the graph through the key points.

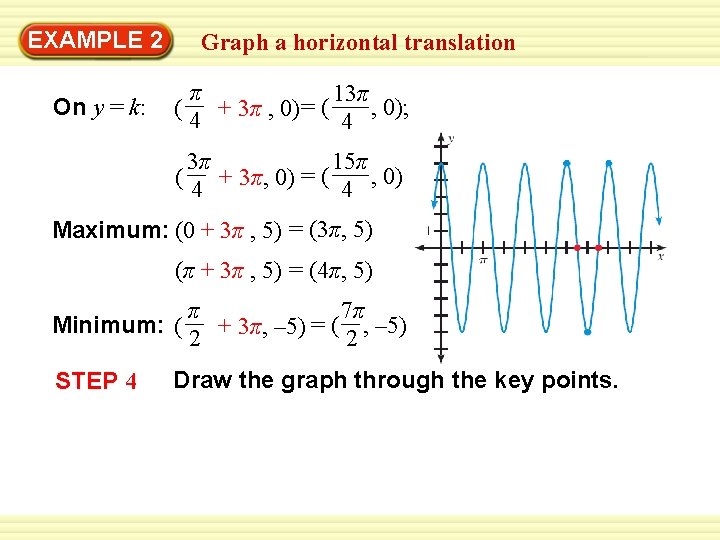
EXAMPLE 2 Graph a horizontal translation Graph y = 5 cos 2(x – 3π ). SOLUTION STEP 1 Identify the amplitude, period, horizontal shift, and vertical shift. Amplitude: a = 5 Horizontal shift: h = 3π Period: 2 π = π b 2 Vertical shift: k = 0 STEP 2 Draw the midline of the graph. Because k = 0, the midline is the x-axis. STEP 3 Find the five key points.

EXAMPLE 2 On y = k: Graph a horizontal translation π 13π = ( , 0); ( 4 + 3π , 0) 4 3π 15π = ( , 0) ( 4 + 3π, 0) 4 Maximum: (0 + 3π , 5) = (3π, 5) (π + 3π , 5) = (4π, 5) π 7π = ( , – 5) Minimum: ( 2 + 3π, – 5) 2 STEP 4 Draw the graph through the key points.

EXAMPLE 3 Graph a model for circular motion Ferris Wheel Suppose you are riding a Ferris wheel that turns for 180 seconds. Your height h (in feet) above the ground at any time t (in seconds) can be modeled by the equation h = 85 sin π (t – 10) + 90. 20 a. Graph your height above the ground as a function of time. b. What are your maximum and minimum heights?

EXAMPLE 3 Graph a model for circular motion SOLUTION a. 2π The amplitude is 85 and the period is π = 40. 20 180 The wheel turns = 4. 5 times in 180 seconds, 40 so the graph below shows 4. 5 cycles. The five key points are (10, 90), (20, 175), (30, 90), (40, 5), and (50, 90).

EXAMPLE 3 Graph a model for circular motion b. Your maximum height is 90 + 85 = 175 feet and your minimum height is 90 – 85 = 5 feet.

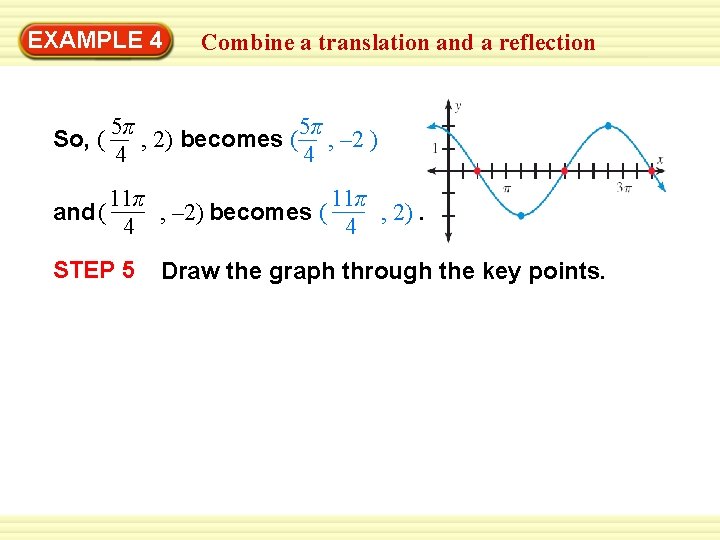
EXAMPLE 4 Combine a translation and a reflection Graph y = – 2 sin 2 (x – π ). 3 2 SOLUTION STEP 1 Identify the amplitude, period, horizontal shift, and vertical shift. π Amplitude: a = – 2 = 2 Horizontal shift: h = 2 2π 2π period : b = 2 = 3π Vertical shift: k = 0 3 STEP 2 Draw the midline of the graph. Because k = 0, the midline is the x-axis.

EXAMPLE 4 Combine a translation and a reflection Find the five key points of y = – 2 sin 2 (x – π ). 3 2 π 3π π On y = k: (0 + π , 0) = ( , 0); ( + 2 , 0) = (2π, 0) 2 2 2 STEP 3 π 7π (3π + , 0) = ( , 0) 2 2 3π π 5π , 2) = ( ( + , 2) Maximum: 4 2 4 9π π 11π , – 2) Minimum: ( + 2 , – 2) = ( 4 4 STEP 4 Reflect the graph. Because a < 0, the graph is reflected in the midline y = 0.

EXAMPLE 4 Combine a translation and a reflection So, ( 5π 5π , 2) becomes ( , – 2 ) 4 4 and ( 11π becomes ( , 2). , – 2) 4 4 STEP 5 Draw the graph through the key points.

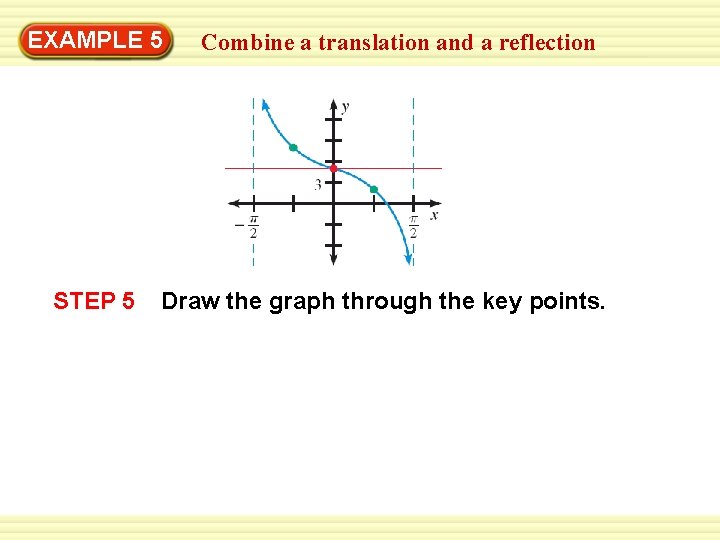
EXAMPLE 5 Combine a translation and a reflection Graph y = – 3 tan x + 5. SOLUTION STEP 1 Identify the period, horizontal shift, and vertical shift. Period: π Horizontal shift: h = 0 Vertical shift: k = 5 STEP 2 Draw the midline of the graph, y = 5. STEP 3 Find the asymptotes and key points of y = – 3 tan x + 5.

EXAMPLE 5 Combine a translation and a reflection Asymptotes: π π – = = x= = – ; x 2 2 1 On y = k: (0, 0 + 5) = (0, 5) π π , 8) π π ( ( , 3 + 5) = Halfway points: (– , – 3 + 5) = (– , 2); 4 4 STEP 4 Reflect the graph. Because a < 0, the graph is reflected in the midline y = 5. π , 2) becomes (– π , 8) 4 4 π π ( , 2). ( , 8) and becomes 4 4 So, (–

EXAMPLE 5 STEP 5 Combine a translation and a reflection Draw the graph through the key points.

EXAMPLE 6 Model with a tangent function Glass Elevator You are standing 120 feet from the base of a 260 foot building. You watch your friend go down the side of the building in a glass elevator. Write and graph a model that gives your friend’s distance d (in feet) from the top of the building as a function of the angle of elevation q.

EXAMPLE 6 Model with a tangent function SOLUTION Use a tangent function to write an equation relating d and q. opp 260 – d tan q = = adj 120 tan q = 260 – d 120 tan q – 260 = – d – 120 tan q + 260 = d Definition of tangent Multiply each side by 120. Subtract 260 from each side. Solve for d. The graph of d = – 120 tan q + 260 is shown at the right.