Exam III Physics 101 Lecture 19 Elasticity and

Exam III Physics 101: Lecture 19 Elasticity and Oscillations II Physics 101: Lecture 19, Pg 1

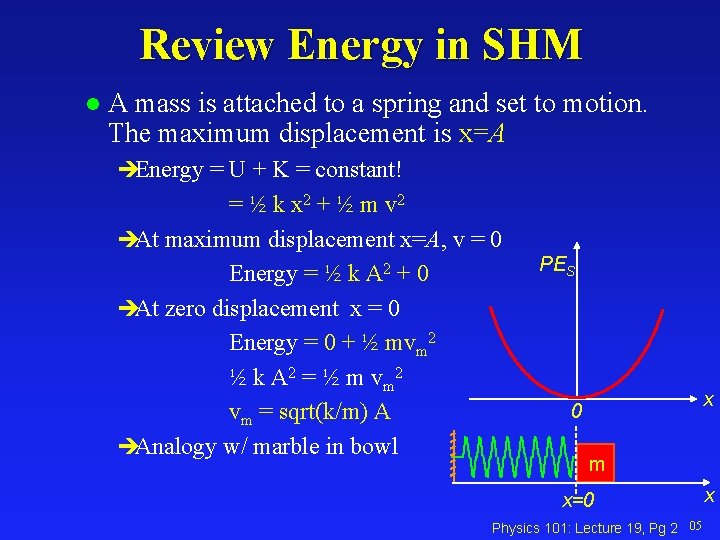
Review Energy in SHM l A mass is attached to a spring and set to motion. The maximum displacement is x=A èEnergy = U + K = constant! = ½ k x 2 + ½ m v 2 èAt maximum displacement x=A, v = 0 Energy = ½ k A 2 + 0 èAt zero displacement x = 0 Energy = 0 + ½ mvm 2 ½ k A 2 = ½ m v m 2 vm = sqrt(k/m) A èAnalogy w/ marble in bowl PES x 0 m x=0 Physics 101: Lecture 19, Pg 2 05 x

Simple Harmonic Motion: Quick Review x(t) = [A]cos( t) v(t) = -[A ]sin( t) a(t) = -[A 2]cos( t) x(t) = [A]sin( t) OR v(t) = [A ]cos( t) a(t) = -[A 2]sin( t) xmax = A Period = T (seconds per cycle) vmax = A Frequency = f = 1/T (cycles per second) amax = A 2 Angular frequency = = 2 f = 2 /T Physics 101: Lecture 19, Pg 3 19

Period T of a Spring l Simple Harmonic Oscillator è = 2 f = 2 / T èx(t) = [A] cos( t) èv(t) = -[A ] sin( t) èa(t) = -[A 2] cos( t) Demos: A, m, k dependence l For a Spring F = -kx èamax = (k/m) A èA 2 = (k/m) A = sqrt(k/m) Physics 101: Lecture 19, Pg 4 23

Question If the amplitude of the oscillation (same block and same spring) is doubled, how would the period of the oscillation change? (The period is the time it takes to make one complete oscillation) A. The period of the oscillation would double. B. The period of the oscillation would be halved C. The period of the oscillation would stay the same x +2 A t -2 A Physics 101: Lecture 19, Pg 5 27

Vertical Mass and Spring l If we include gravity, there are two forces acting on mass. With mass, new equilibrium position has spring stretched d èSF = kd – mg = 0 d = mg/k Let this point be y=0 èSF = k(d-y) – mg = -k y èSame as horizontal! SHO èNew equilibrium position y=-d Physics 101: Lecture 19, Pg 6 31

Vertical Spring Question If the springs were vertical, and stretched the same distance d from their equilibrium position and then released, which would have the maximum kinetic energy? 1) M 2) 2 M 3) Same PE = 1/2 k y 2 Y=0 Physics 101: Lecture 19, Pg 7 33

Pendulum Motion l For small angles èT = mg èTx = -mg (x/L) Note: F proportional to x! èS Fx = m ax -mg (x/L) = m ax ax = -(g/L) x èRecall for SHO a = - 2 x L T = sqrt(g/L) T = 2 sqrt(L/g) Period does not depend on A, or m! x m mg Physics 101: Lecture 19, Pg 8 37

Example: Clock l If we want to make a grandfather clock so that the pendulum makes one complete cycle each sec, how long should the pendulum be? Physics 101: Lecture 19, Pg 9

Question 1 Suppose a grandfather clock (a simple pendulum) runs slow. In order to make it run on time you should: 1. Make the pendulum shorter 2. Make the pendulum longer Physics 101: Lecture 19, Pg 10 38

Elevator ACT A pendulum is hanging vertically from the ceiling of an elevator. Initially the elevator is at rest and the period of the pendulum is T. Now the pendulum accelerates upward. The period of the pendulum will now be 1. greater than T 2. equal to T 3. less than T “Effective g” is larger when accelerating upward (you feel heavier) Physics 101: Lecture 19, Pg 11 44

Question Imagine you have been kidnapped by space invaders and are being held prisoner in a room with no windows. All you have is a cheap digital wristwatch and a pair of shoes (including shoelaces of known length). Explain how you might figure out whether this room is on the earth or on the moon Physics 101: Lecture 19, Pg 12 50

Summary l Simple Harmonic Motion èOccurs when have linear restoring force F= -kx èx(t) = [A] cos( t) èv(t) = -[A ] sin( t) èa(t) = -[A 2] cos( t) l Springs èF = -kx èU = ½ k x 2 è = sqrt(k/m) l Pendulum (Small oscillations) è = sqrt(L/g) Physics 101: Lecture 19, Pg 13 50