Evolutionary of the VariableLength Multiobjective Genetic Algorithm December

Evolutionary of the Variable-Length Multi-objective Genetic Algorithm 李宗南 國立中山大學 資訊 程學系 December 3, 2008

2 Outline • A tale of single objective optimization and multi-objective optimization • The single genetic algorithm • The multi-objective genetic algorithm • The variable length multi-objective optimization • Applications - Aircraft routing - Placement of heterogeneous wireless transmitters • Conclusions
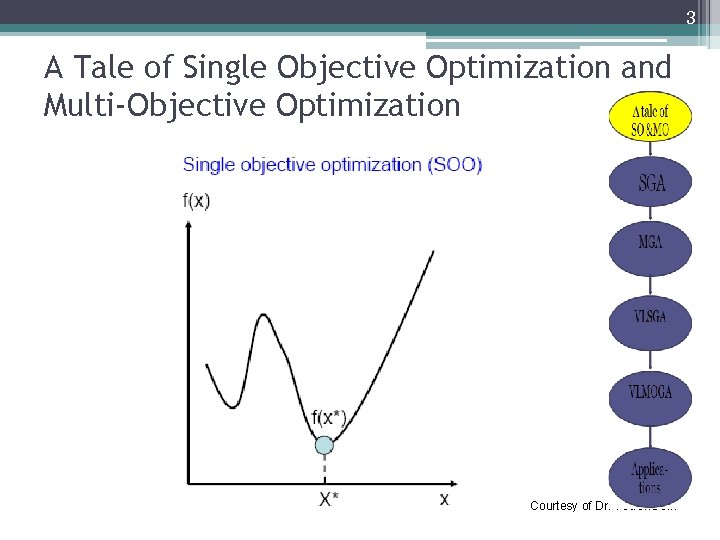
3 A Tale of Single Objective Optimization and Multi-Objective Optimization Courtesy of Dr. Yoa. Chu Jin

Single Objective Optimization Given: a function f : A → R from some set A to the real numbers Sought: an element x 0 in A such that f(x 0) ≤ f(x) for all x in A ("minimization") or such that f(x 0) ≥ f(x) for all x in A ("maximization").

5 Algorithms for Single Objective Optimization Gradient descent aka steepest descent or steepest ascent Hill climbing Simulated annealing Quantum annealing Tabu search Beam search Genetic algorithms Ant colony optimization Evolution strategy Stochastic tunneling Differential evolution Particle swarm optimization Harmony search Bees algorithm Dynamic relaxation
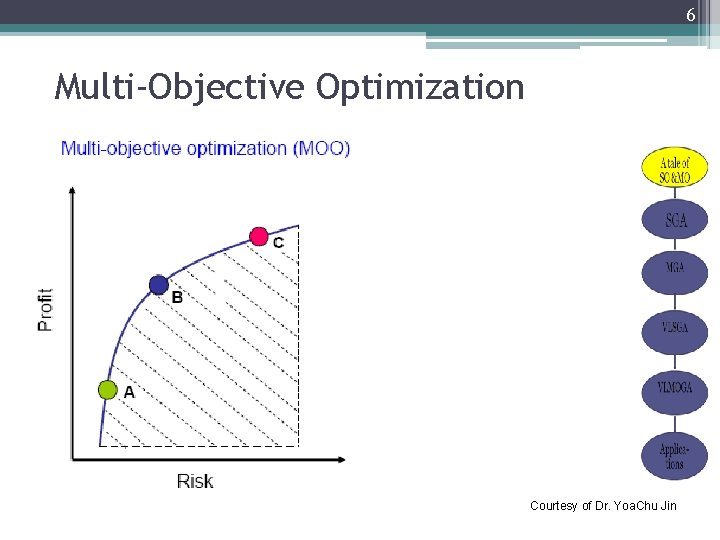
6 Multi-Objective Optimization Courtesy of Dr. Yoa. Chu Jin

7 Multi-Objective Optimization m= 1 , single objective optimization Courtesy of Dr. Yoa. Chu Jin

8 Solutions for Multi-objective Optimization 8 • Map into a single objective optimization by a weighted sum • The multi-objective approach (rank-based fitness assignment method) to evaluate each objective individually

9 Comparison of the single objective approach and the multi-objective approach SO + simple - Hard to determine weight for each objective. - Hard to prevent some objectives from dominating others. MO + Have the ideal situation where each objective function attains a satisfactory level. + Have the flexibility to achieve different levels of tradeoff. - Not so easy to solve.
10 Single GA
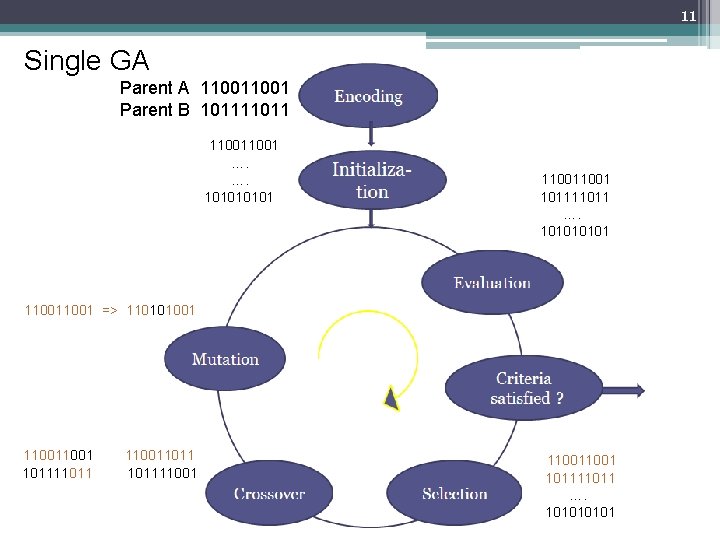
11 Single GA Parent A 11001 Parent B 101111011 11001 …. 10101 11001 101111011 …. 10101 11001 => 110101001 11001101111011 101111001 101111011 …. 10101
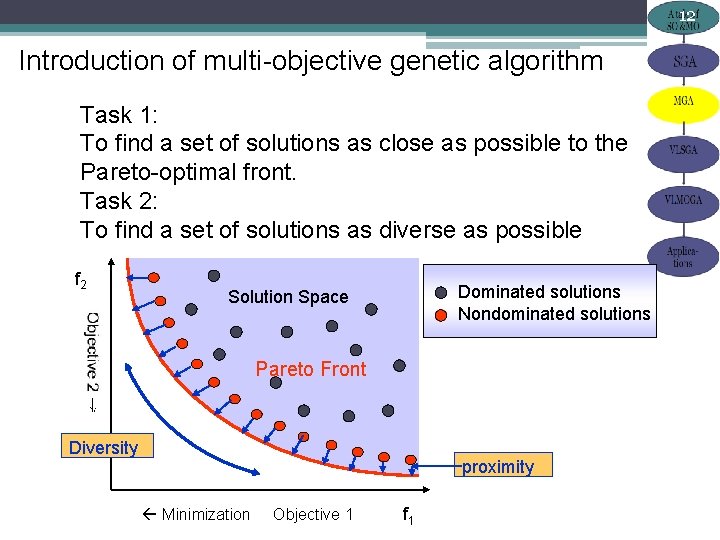
12 Introduction of multi-objective genetic algorithm Task 1: To find a set of solutions as close as possible to the Pareto-optimal front. Task 2: To find a set of solutions as diverse as possible f 2 Dominated solutions Nondominated solutions Solution Space Pareto Front Diversity proximity Minimization Objective 1 f 1

13 The variable length genetic algorithm Why Variable-Length GAs (VLGAs)? The number of solutions is not fixed. i. e. Fixed Length GAs must know number of variables a priori Ex: Finding number of base stations for a given region Ex: Finding rules for autonomous agents

14 Evolutionary of the variable length multiobjective optimization The number of solutions is not fixed. It is a multi-objective optimization problem We would like to solve the problem by GA
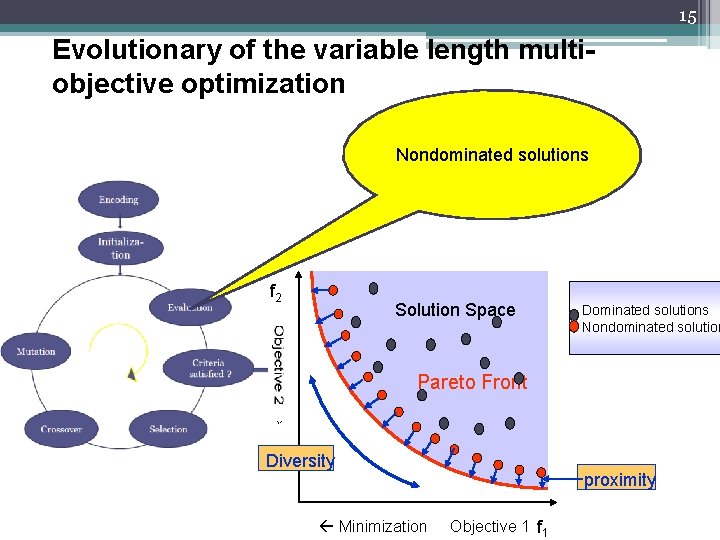
15 Evolutionary of the variable length multiobjective optimization Nondominated solutions f 2 Solution Space Dominated solutions Nondominated solution Pareto Front Diversity Minimization Objective 1 f 1 proximity
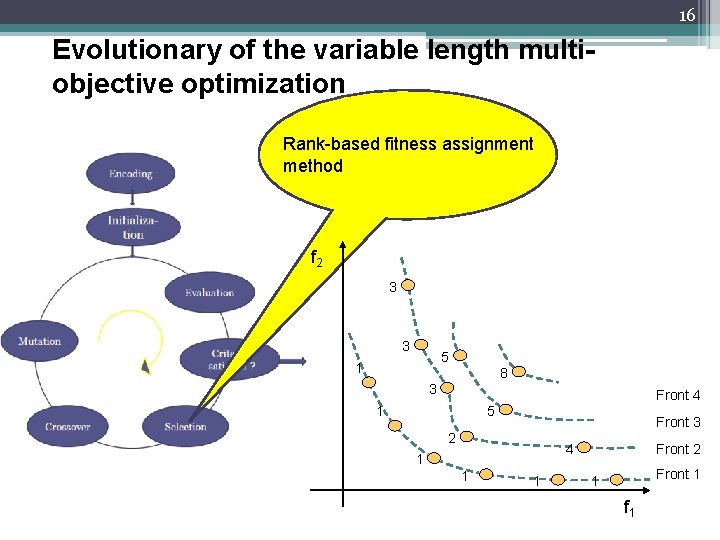
16 Evolutionary of the variable length multiobjective optimization Rank-based fitness assignment method f 2 3 3 5 1 8 3 Front 4 1 5 Front 3 2 4 1 1 1 Front 2 Front 1 1 f 1
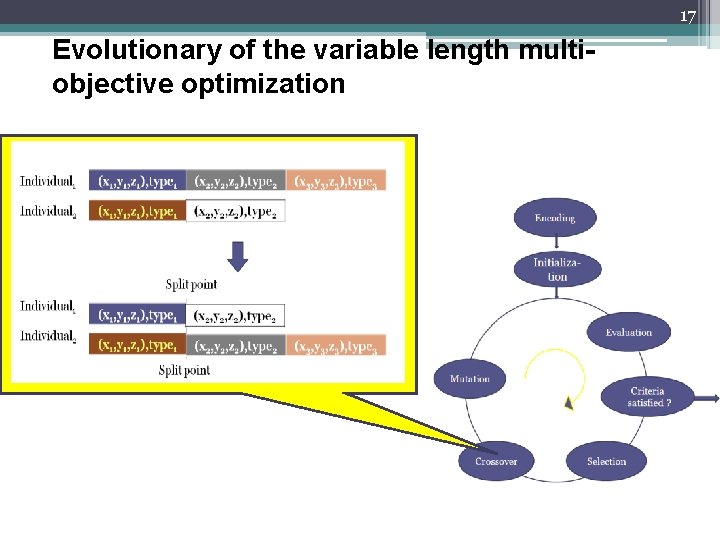
17 Evolutionary of the variable length multiobjective optimization

18 Applications MOGA - Aircraft routing VLMOGA - Placement of heterogeneous wireless transmitters

19 Application 1 Aircraft Routing using Multiobjective Genetic Algorithm

20 Problem Description • Aircraft routing ▫ A given set of flights a group of aircrafts ▫ Available amount of aircrafts

21 Aircraft Routing (1/2) Timetable assign to aircrafts Flight ID Dep. Time Arv. Time Origin Destination f 1 f 2 f 3 f 4 f 5 f 6 f 7 f 8 09: 15 19: 00 14: 00 11: 20 22: 00 16: 30 08: 10 20: 35 09: 50 19: 35 14: 35 11: 55 22: 50 17: 20 09: 00 21: 25 KHH TSA MZG TSA TNN TSA KHH TSA MZG TSA TNN TSA f 9 18: 00 18: 50 TNN TSA f 10 15: 30 16: 20 TSA TNN Flight ID Dep. Time Arv. Time f 11 f 12 f 13 f 14 f 15 f 16 f 17 f 18 f 19 f 20 09: 30 19: 10 14: 10 10: 20 18: 00 15: 30 08: 20 18: 35 13: 00 10: 20 10: 05 19: 45 14: 45 10: 55 18: 50 16: 20 09: 20 19: 25 13: 35 10: 55 Origin Destination HUN TSA MZG TSA TXG TSA KHH MZG TSA HUN TSA MZG TSA TXG TSA TSA MZG
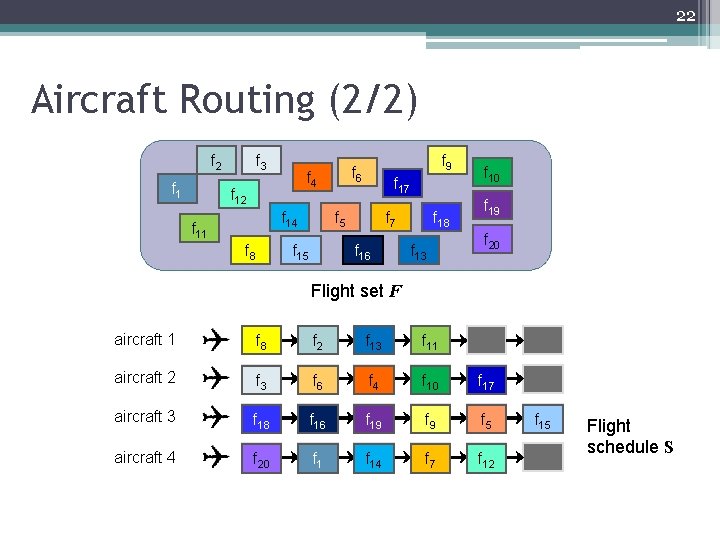
22 Aircraft Routing (2/2) f 2 f 1 f 3 f 4 f 12 f 14 f 11 f 8 f 9 f 6 f 17 f 5 f 15 f 7 f 16 f 18 f 13 f 10 f 19 f 20 Flight set F aircraft 1 f 8 f 2 f 13 f 11 aircraft 2 f 3 f 6 f 4 f 10 f 17 aircraft 3 f 18 f 16 f 19 f 5 aircraft 4 f 20 f 14 f 7 f 12 f 15 Flight schedule S

23 Notations • Let α, β, ω, and γ represent ▫ ▫ α: number of aircrafts β: maximal number of flights per aircraft ω: number of airports γ: number of daily flights, respectively. • Set of flights: F = {fi|1 ≤ i ≤ γ} • Set of airports: P = {pj|1 ≤j ≤ ω} P= {台北松山機場、 高雄小港、 台中、 台南 、馬公、 金門}

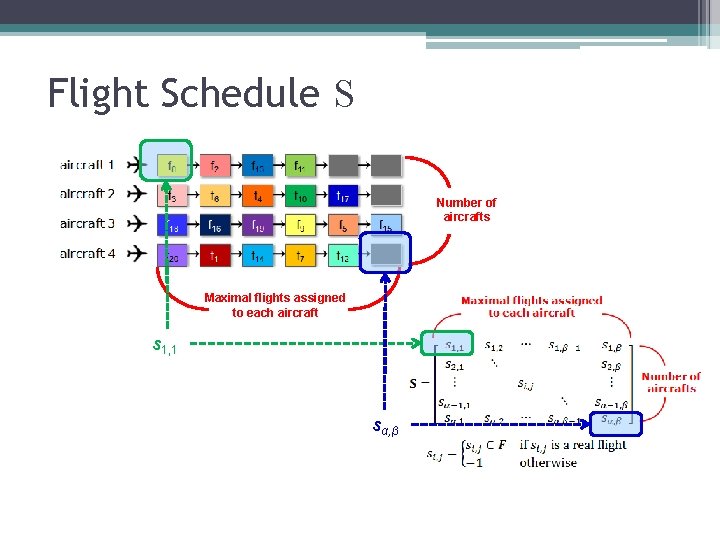
24 , Associate Information of One Flight The flight schedule S can be represented as: si, j: the jth flight assigned to the ith aircraft : origin of si, j, where : destination of si, j, where : departure time from : arrival time in

25 Definition of a Flight Schedule Maximal flights assigned to each aircraft Number of aircrafts
Flight Schedule S Number of aircrafts Maximal flights assigned to each aircraft s 1, 1 sα, β 2 6

27 Objectives o Objectives: Subject to • Ground turn-around time objective • Flow balance objective

28 Ground Turn-around Objective(1) Legal ground turn-around time: TGH
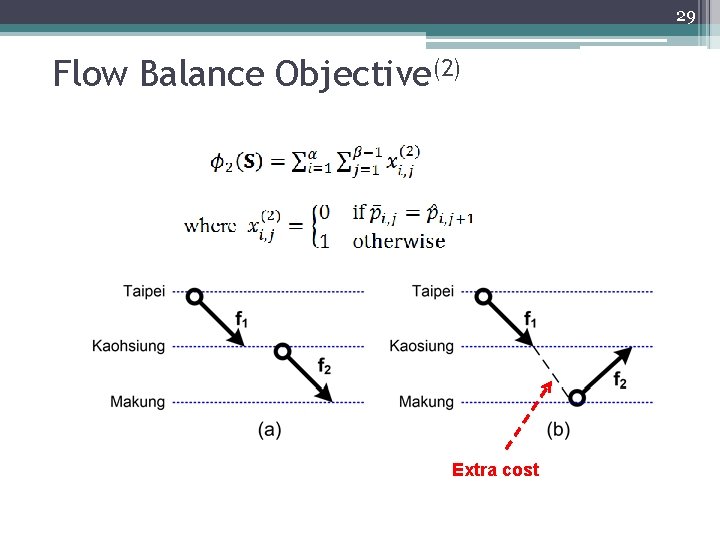
29 Flow Balance Objective(2) Extra cost
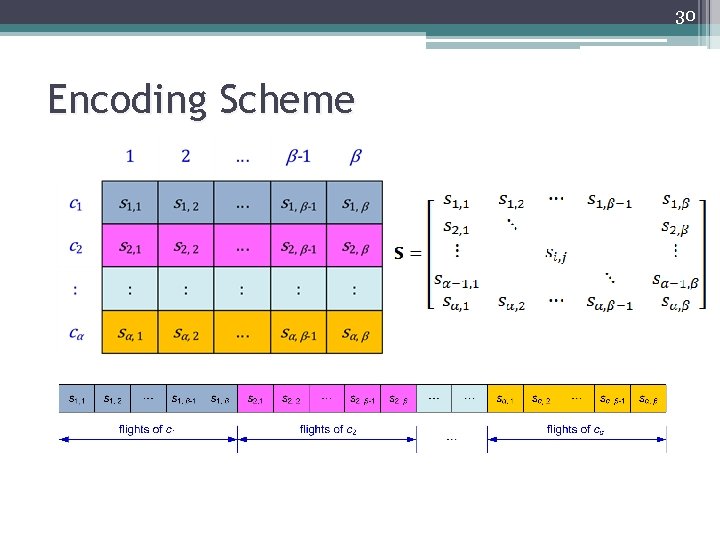
30 Encoding Scheme
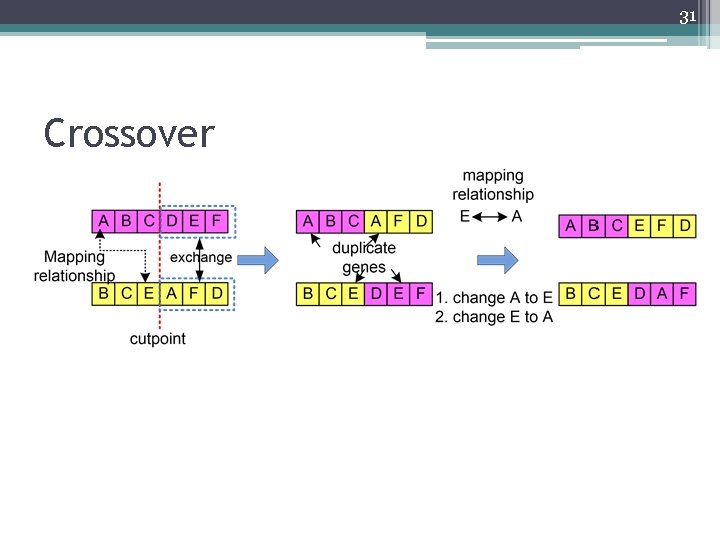
31 Crossover
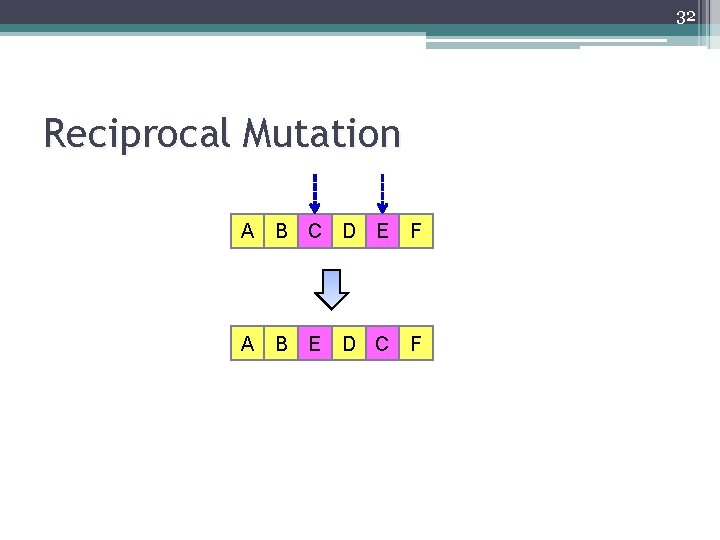
32 Reciprocal Mutation A B C D E F A B F E D C
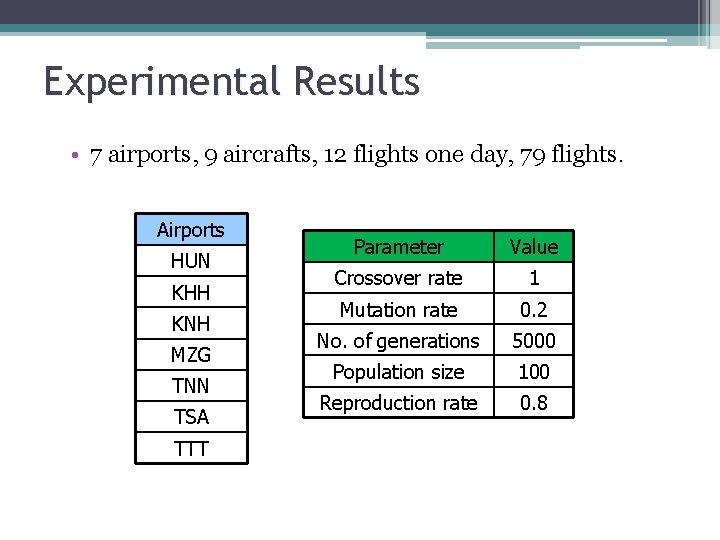
Experimental Results • 7 airports, 9 aircrafts, 12 flights one day, 79 flights. Airports HUN KHH KNH MZG TNN TSA Parameter Value Crossover rate 1 Mutation rate 0. 2 No. of generations 5000 Population size 100 Reproduction rate 0. 8 TTT 33
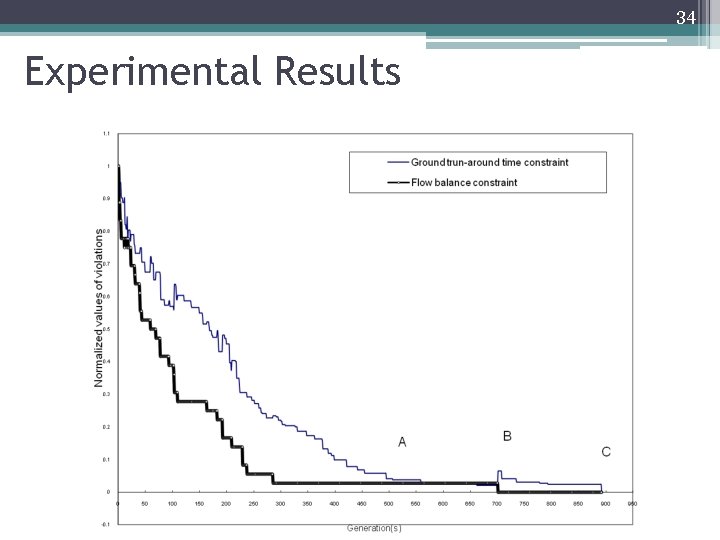
34 Experimental Results
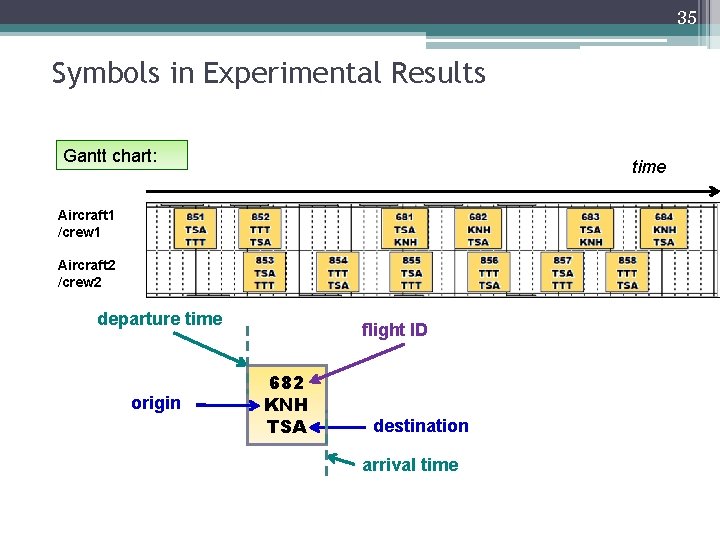
35 Symbols in Experimental Results Gantt chart: time Aircraft 1 /crew 1 Aircraft 2 /crew 2 departure time origin flight ID 682 KNH TSA destination arrival time
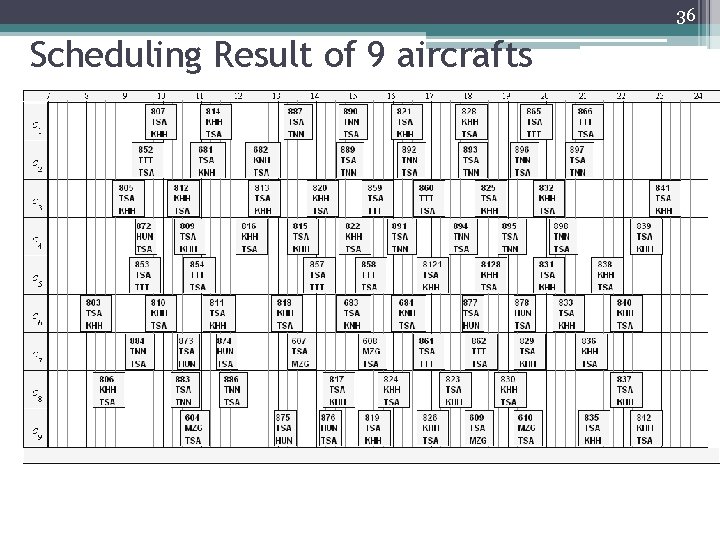
36 Scheduling Result of 9 aircrafts
![37 Scheduling Result of 8 aircrafts Example ε = [ε 1, ε 2] =[k 37 Scheduling Result of 8 aircrafts Example ε = [ε 1, ε 2] =[k](http://slidetodoc.com/presentation_image/5e0751c2f3734bf8661bc255a5543e0e/image-37.jpg)
37 Scheduling Result of 8 aircrafts Example ε = [ε 1, ε 2] =[k 1 × α × TGH, k 2× α] = [1 × 8 × 25, 1 × 8] = [200, 8] Original value Φ(S) = [ϕ 1(S), ϕ 2(S)] Values in auxiliary vector of performance indices Λ(S, ε)=[λ(S, ε 1), λ(S, ε 2)] Result 1 [195, 0] [0, 0] Result 2 [190, 1] [0, 0] Result 3 [185, 2] [0, 0]

38 Scheduling Result of 8 aircrafts Result 1 Result 2 Result 3
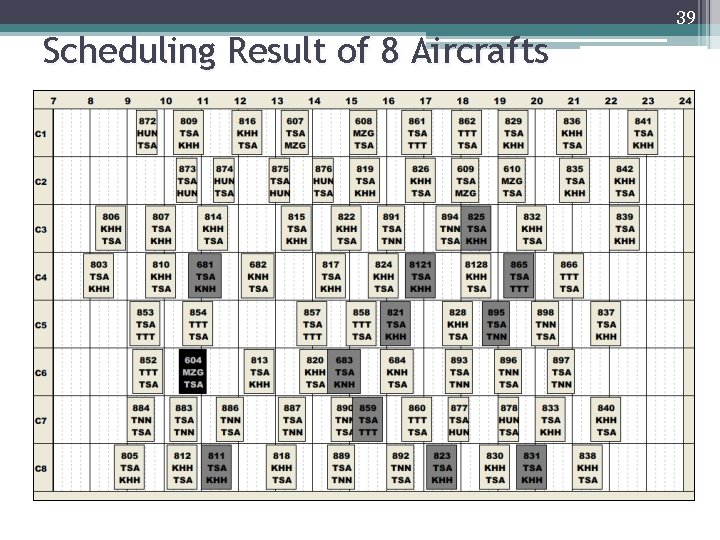
39 Scheduling Result of 8 Aircrafts
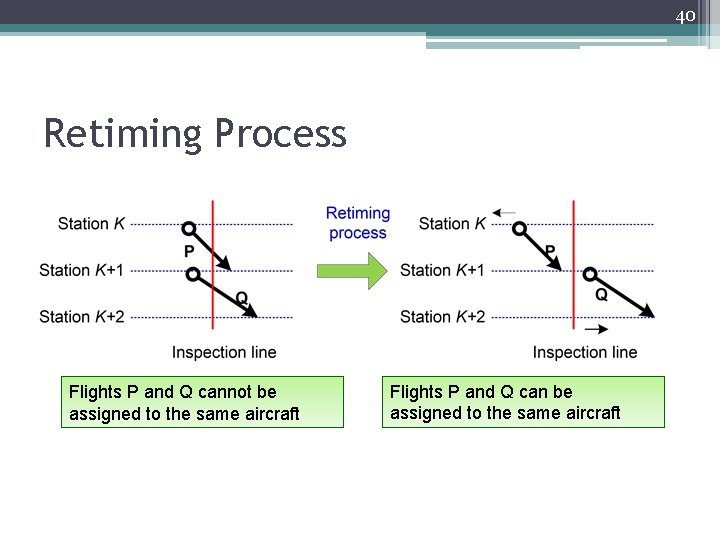
40 Retiming Process Flights P and Q cannot be assigned to the same aircraft Flights P and Q can be assigned to the same aircraft
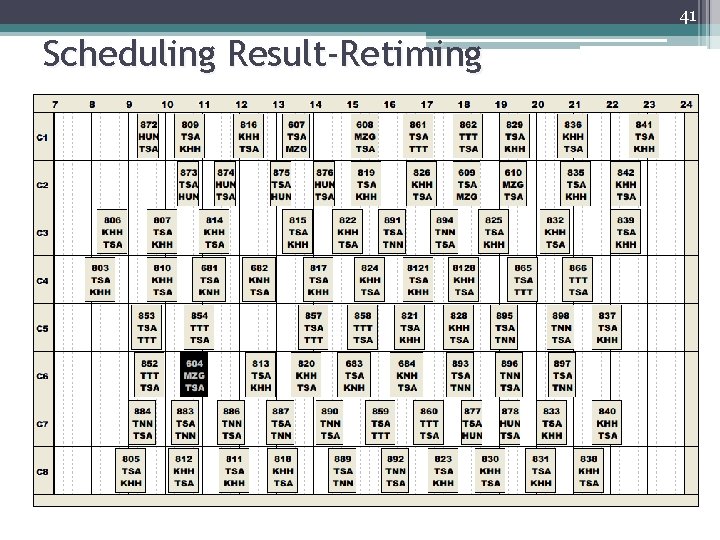
41 Scheduling Result-Retiming

42 Application 2: Heterogeneous Wireless Transmitter Placement with Multiple Constraints based on the Variable-Length Multi-objective Genetic Algorithm

43 Problem statement Choose a set of heterogeneous wireless transmitters to place on the designed space to fulfill certain design requirements such as Position, power, capacity, frequency channel assignment, overlap, data rate demand, population density, cost and coverage Evolutionary multiobjective optimization for base station transmitter placement with frequency assignment, IEEE Trans. on Evolutionary Computation, 2003
44 Introduction (cont. ) 23 meters 15 meters
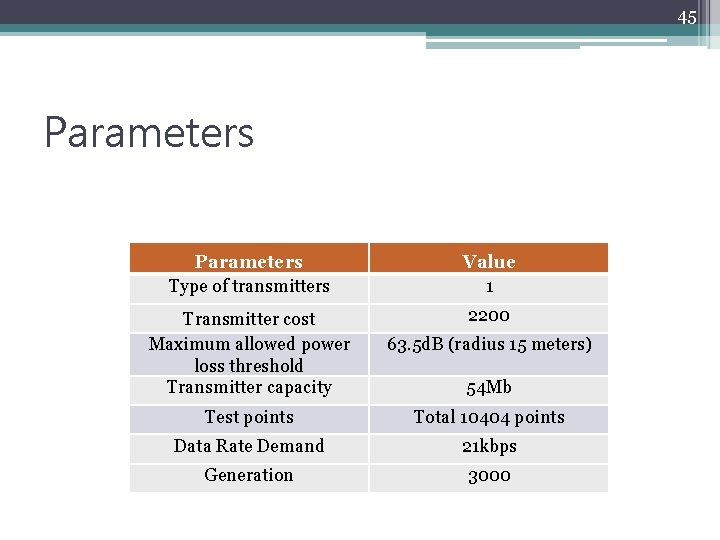
45 Parameters Type of transmitters Value 1 Transmitter cost Maximum allowed power loss threshold Transmitter capacity 2200 63. 5 d. B (radius 15 meters) Test points Total 10404 points Data Rate Demand 21 kbps Generation 3000 54 Mb
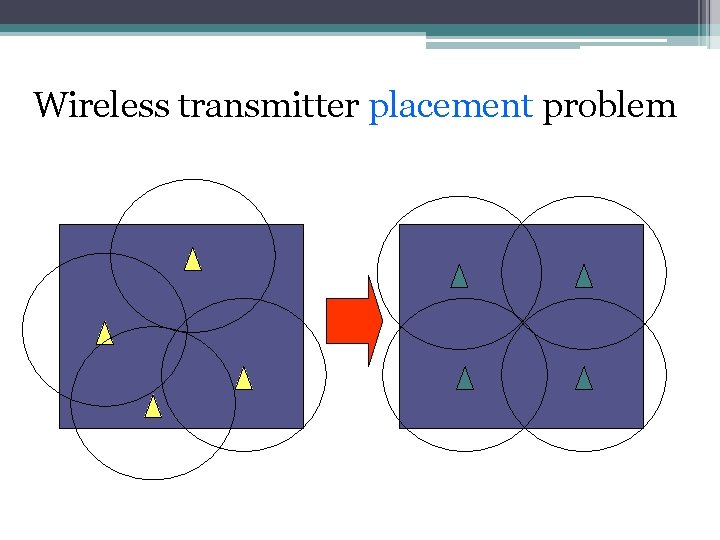
Wireless transmitter placement problem

47 Problem Definition • Model ▫ Map, receiver, transmitter • Receiver ▫ Position, data rate demand, sensitivity • Transmitter ▫ Position, type=(cost, power, capacity)

48 Path Loss Propagation Models 1. Free space path loss model 2. Log-distance path loss model with shadowing effect 3. ECC-33 model

49 Objectives • • Coverage Cost Data Rate Demand Overlap
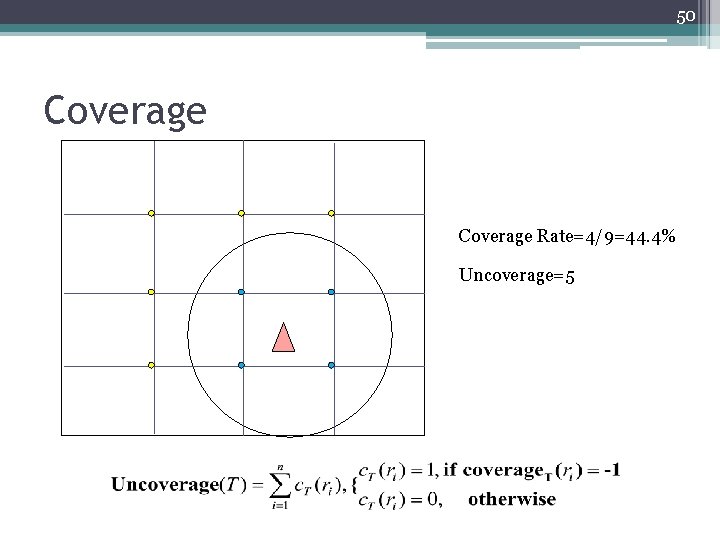
50 Coverage Rate=4/9=44. 4% Uncoverage=5

51 Cost • Cost=1000+300*2 =1600 Cost=1000 Cost=300
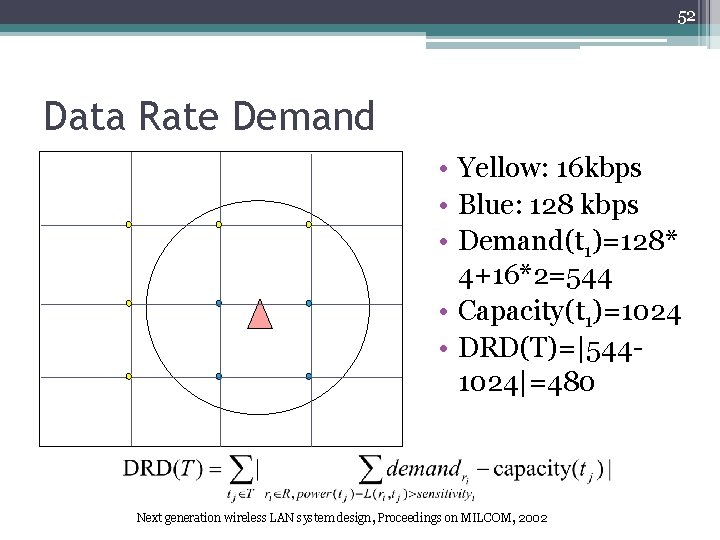
52 Data Rate Demand • Yellow: 16 kbps • Blue: 128 kbps • Demand(t 1)=128* 4+16*2=544 • Capacity(t 1)=1024 • DRD(T)=|5441024|=480 Next generation wireless LAN system design, Proceedings on MILCOM, 2002
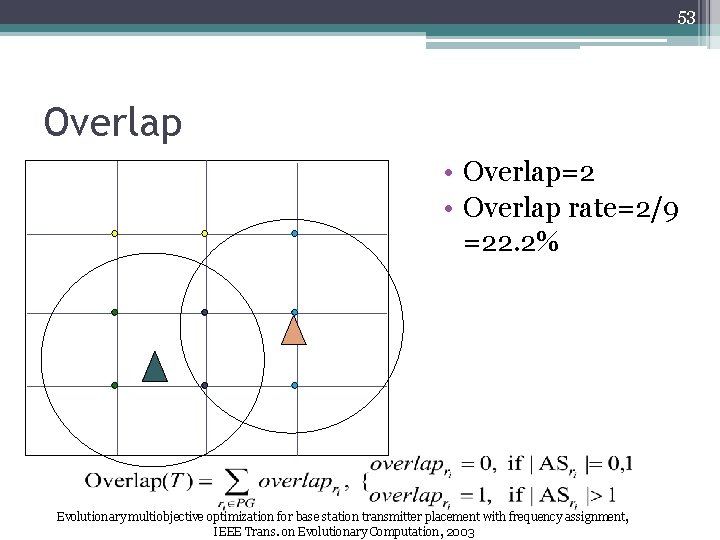
53 Overlap • Overlap=2 • Overlap rate=2/9 =22. 2% Evolutionary multiobjective optimization for base station transmitter placement with frequency assignment, IEEE Trans. on Evolutionary Computation, 2003

54 Objectives • Minimize • Subject to
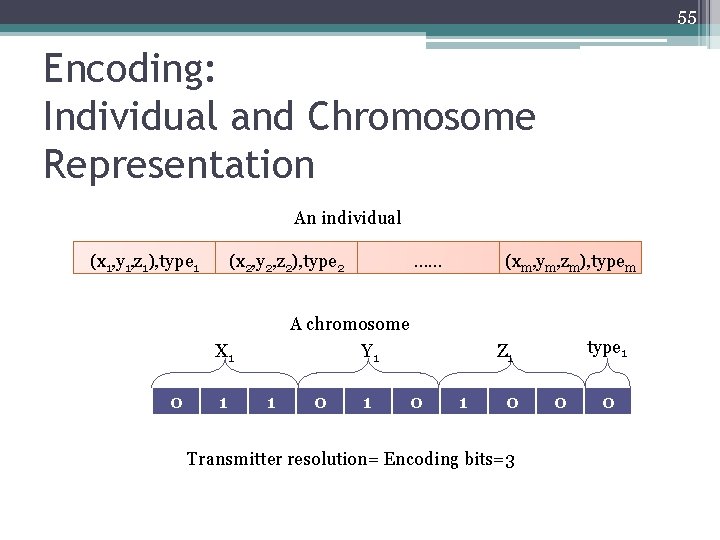
55 Encoding: Individual and Chromosome Representation An individual (x 1, y 1, z 1), type 1 (x 2, y 2, z 2), type 2 1 (xm, ym, zm), typem A chromosome Y 1 X 1 0 …… 1 0 1 type 1 Z 1 0 Transmitter resolution= Encoding bits=3 0 0

56 Population Initialization • Temporary upper bound UB=10 • Random number=4 (1~10) type 1 type 3 type 2 type 1 Flowchart

57 Types of crossover • Uniform crossover for chromosome ▫ Change the position and type of transmitter • Variable-length one-point crossover ▫ Change the length of individual

58 Uniform Crossover for chromosome Individual 1 (x 1, y 1, z 1), type 1 Individual 2 (x 1, y 1, z 1), type 1 (x 2, y 2, z 2), type 2 (x 3, y 3, z 3), type 3
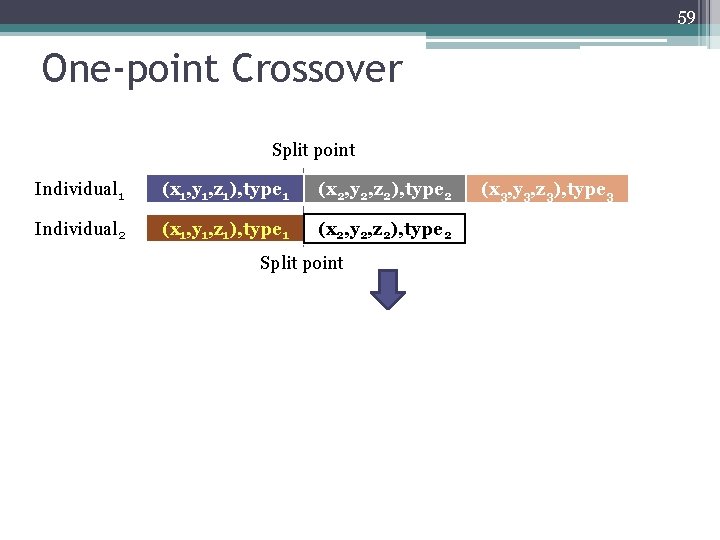
59 One-point Crossover Split point Individual 1 (x 1, y 1, z 1), type 1 (x 2, y 2, z 2), type 2 Individual 2 (x 1, y 1, z 1), type 1 (x 2, y 2, z 2), type 2 Split point (x 3, y 3, z 3), type 3
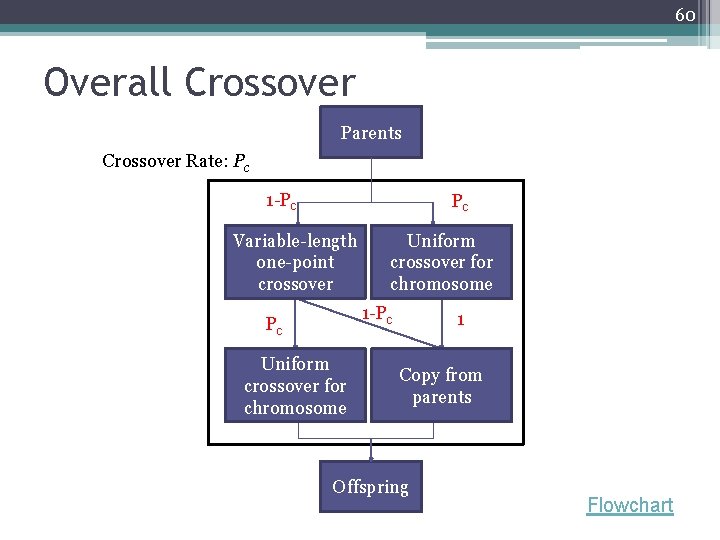
60 Overall Crossover Parents Crossover Rate: Pc 1 -Pc Pc Variable-length one-point crossover Uniform crossover for chromosome 1 -Pc Pc Uniform crossover for chromosome 1 Copy from parents Offspring Flowchart
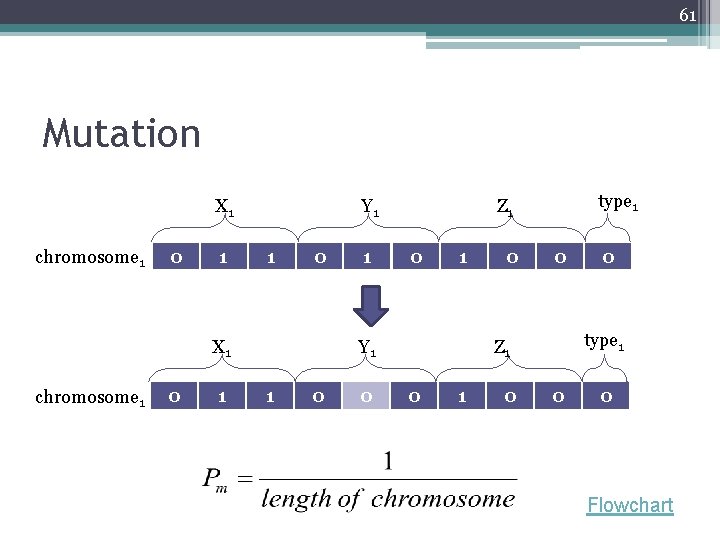
61 Mutation X 1 chromosome 1 0 1 Y 1 1 0 0 type 1 Z 1 0 0 0 0 Flowchart
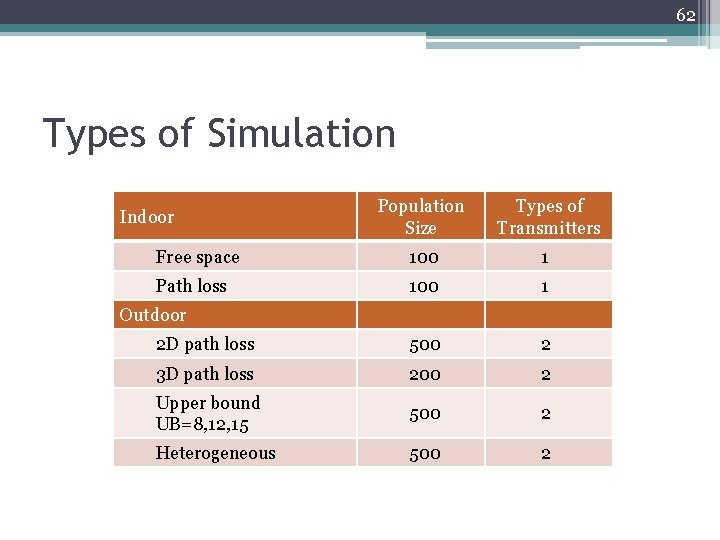
62 Types of Simulation Population Size Types of Transmitters Free space 100 1 Path loss 100 1 2 D path loss 500 2 3 D path loss 200 2 Upper bound UB=8, 12, 15 500 2 Heterogeneous 500 2 Indoor Outdoor
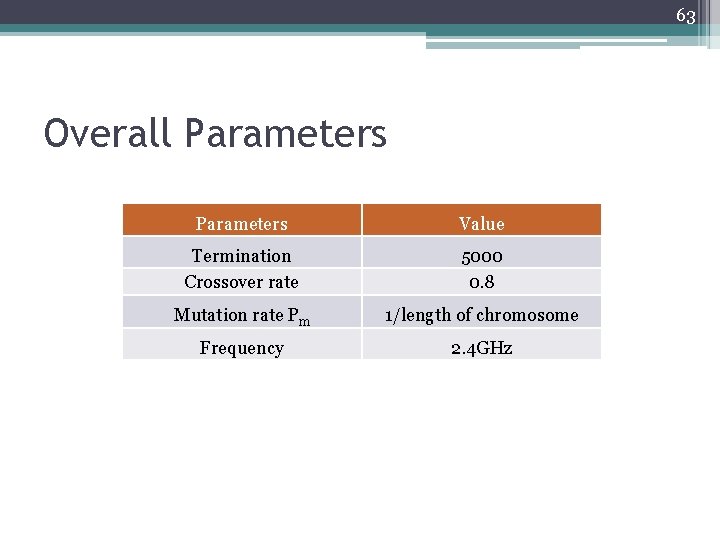
63 Overall Parameters Value Termination Crossover rate 5000 0. 8 Mutation rate Pm 1/length of chromosome Frequency 2. 4 GHz
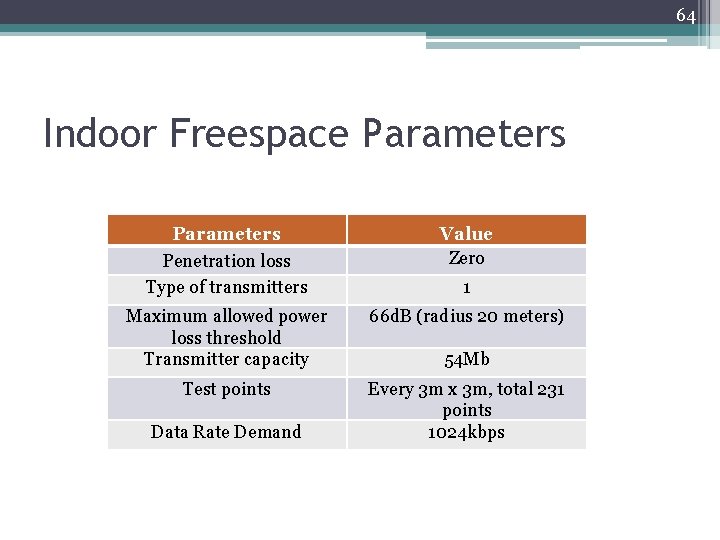
64 Indoor Freespace Parameters Penetration loss Type of transmitters Value Zero 1 Maximum allowed power loss threshold Transmitter capacity 66 d. B (radius 20 meters) Test points Every 3 m x 3 m, total 231 points 1024 kbps Data Rate Demand 54 Mb
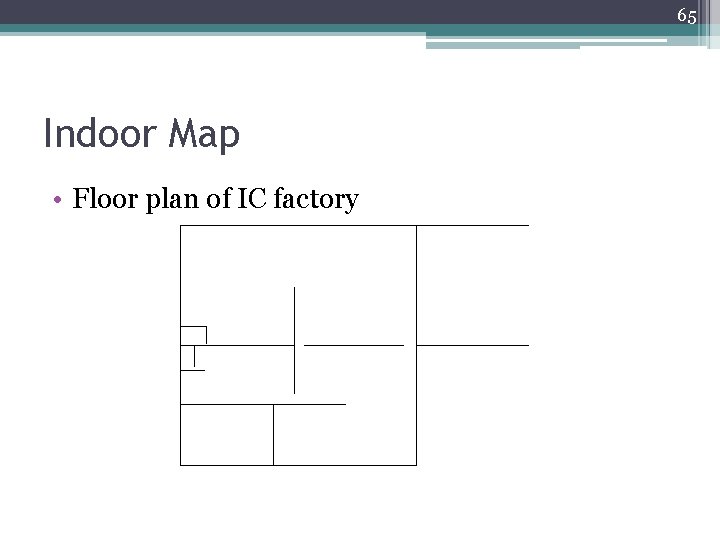
65 Indoor Map • Floor plan of IC factory

66 Indoor Free Space • Threshold 66 d. B (radius 20 meters) Uncoverage 0 Cost 6600 Data rate 83968 demand Overlap 13 BS # 3

67 Indoor Path Loss • Type 1 –cement wall: 3. 3 d. B • Type 2 – thickened cement wall: 6. 5 d. B Uncoverage 0 Cost 13200 Data rate demand 30720 Overlap 48 BS # 6

68 Outdoor Map
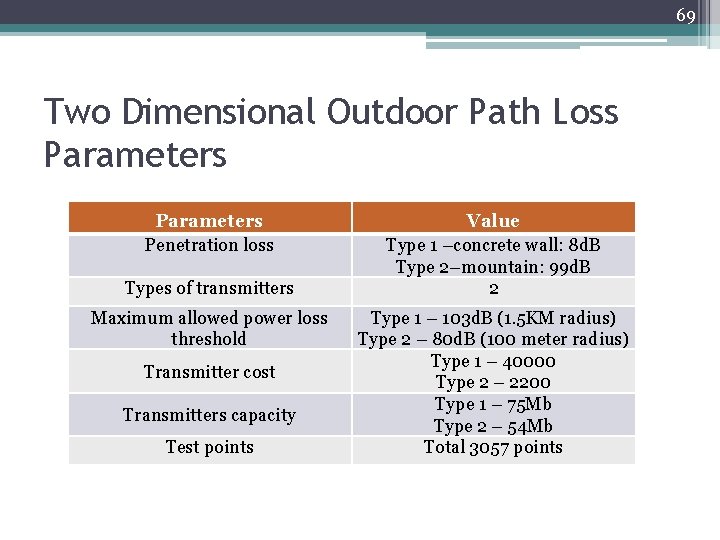
69 Two Dimensional Outdoor Path Loss Parameters Penetration loss Types of transmitters Maximum allowed power loss threshold Transmitter cost Transmitters capacity Test points Value Type 1 –concrete wall: 8 d. B Type 2–mountain: 99 d. B 2 Type 1 – 103 d. B (1. 5 KM radius) Type 2 – 80 d. B (100 meter radius) Type 1 – 40000 Type 2 – 2200 Type 1 – 75 Mb Type 2 – 54 Mb Total 3057 points

70 Outdoor 2 D-Data Rate Demand • Blue: 16 kbps/ 81% • Green: 128 kbps/ 13. 7% • Red: 1024 kbps/ 5. 2%
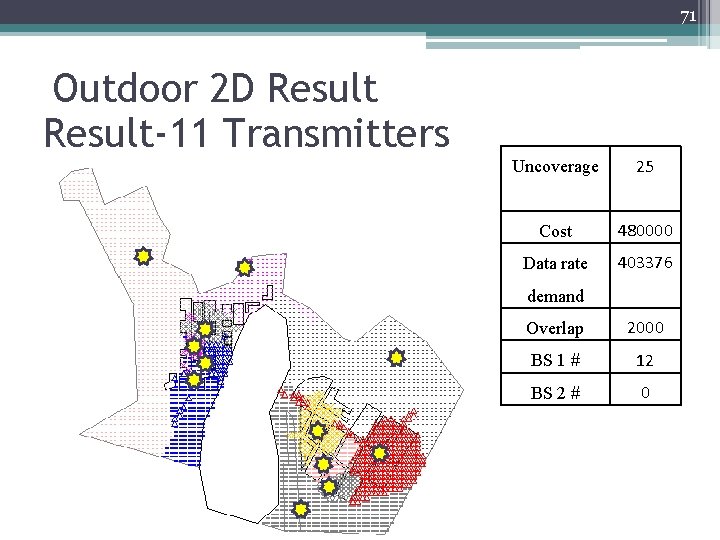
71 Outdoor 2 D Result-11 Transmitters Uncoverage 25 Cost 480000 Data rate 403376 demand Overlap 2000 BS 1 # 12 BS 2 # 0
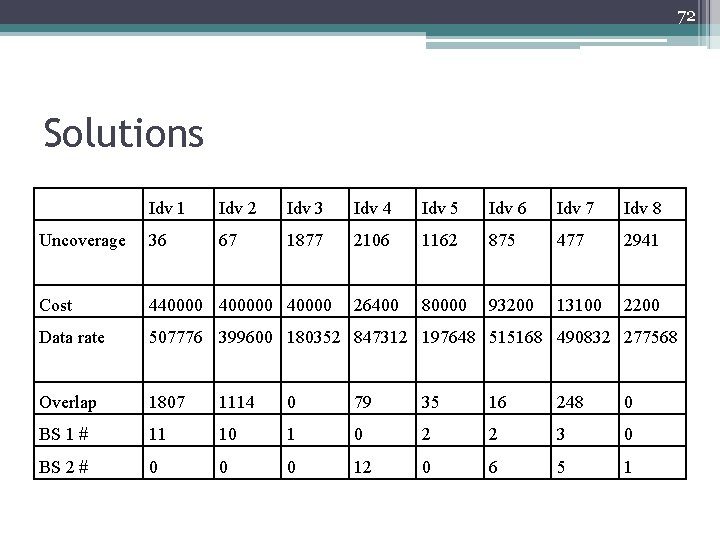
72 Solutions Idv 1 Idv 2 Idv 3 Idv 4 Idv 5 Idv 6 Idv 7 Idv 8 Uncoverage 36 67 1877 2106 1162 875 477 2941 Cost 440000 26400 80000 93200 13100 2200 Data rate 507776 399600 180352 847312 197648 515168 490832 277568 Overlap 1807 1114 0 79 35 16 248 0 BS 1 # 11 10 1 0 2 2 3 0 BS 2 # 0 0 0 12 0 6 5 1
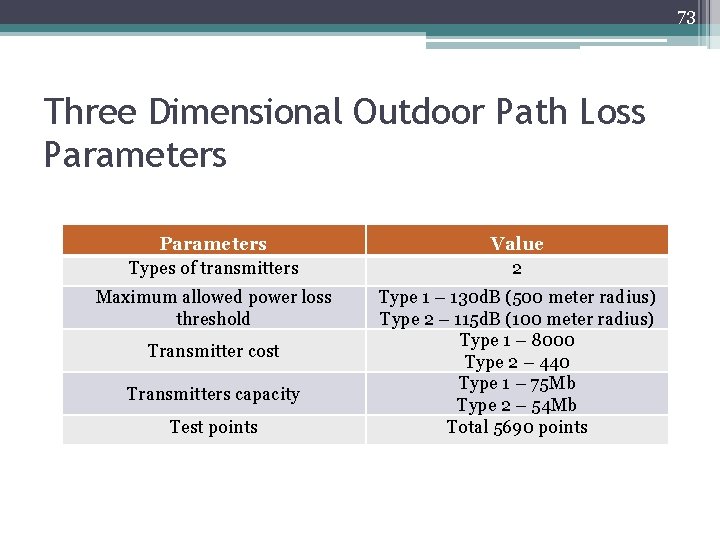
73 Three Dimensional Outdoor Path Loss Parameters Types of transmitters Value 2 Maximum allowed power loss threshold Type 1 – 130 d. B (500 meter radius) Type 2 – 115 d. B (100 meter radius) Type 1 – 8000 Type 2 – 440 Type 1 – 75 Mb Type 2 – 54 Mb Total 5690 points Transmitter cost Transmitters capacity Test points

74 Outdoor 3 D- Data Rate Demand • Blue: 16 kbps/ 57% • Green: 128 kbps/ 28% • Red: 512 kbps/ 15%
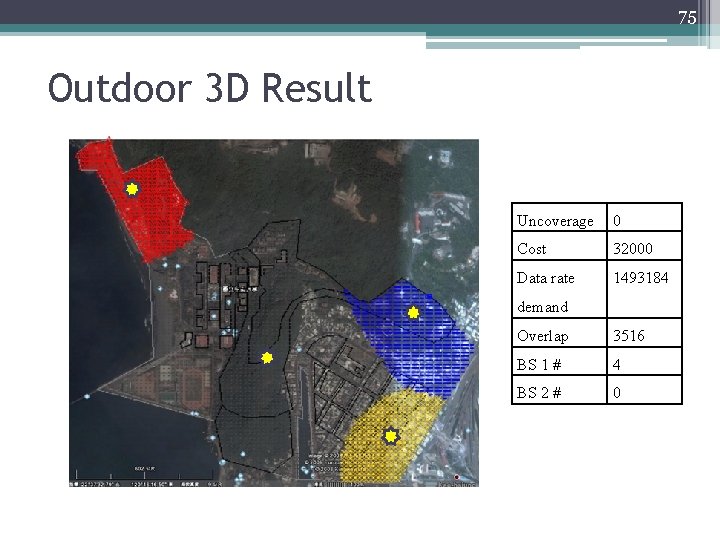
75 Outdoor 3 D Result Uncoverage 0 Cost 32000 Data rate 1493184 demand Overlap 3516 BS 1 # 4 BS 2 # 0

76 Conclusions • Have introduced an evolutionary of the variablelength multi-objective genetic algorithm • Have presented the applications of MOGA and VLMOGA - Flight scheduling - The multiple constraints heterogeneous wireless transmitter placement


78 References 1. 2. 3. 4. Chuan-Kang Ting, Chung-Nan Lee, Hui-Jin Chang, and Jain-Shing Wu “Wireless Heterogeneous Transmitter Placement Using Multi-Objective Variable -Length Genetic Algorithm” accepted to appear in IEEE Trans. on SMC, Part B Ta-Yuan Chow, T. K. Liu and Chung-Nan Lee, Chi-Ruey Jeng “Method of Inequality-Based Multiobjective Genetic Algorithm for Domestic Daily Aircraft Routing ", IEEE Trans. on SMC, Part A. Volume: 38, Issue: 2. March 2008 Sibel Yaman and Chin-Hui Lee“ A Multi-Objective Programming Approach to Compromising Classification Performance Metrics”, IEEE International Workshop on Machine Learning for Signal Processing August 27, 2007 Yaochu Jin, “Evolutionary Multi-Objective Optimization”, Honda Research Institute Europe

79 Question & Suggestion
80 • Thank you for your attentions
- Slides: 80