Evolutionary Algorithms Andrew Cannon Yuki Osada Angeline Honggowarsito

Evolutionary Algorithms Andrew Cannon Yuki Osada Angeline Honggowarsito

Contents What are Evolutionary Algorithms (EAs)? Why are EAs Important? Categories of EAs Mutation Self Adaptation Recombination Selection Application

Evolutionary Algorithms Search methods that mimic the process of natural evolution Principle of “Survival of the Fittest” In each generation, select the fittest parents Re-combine those parents to produce new offspring Perform mutations on the new offspring

Why are EAs Important? Flexibility Adaptable Concept to Problems Problem examples: Travelling Salesman, Knapsack, Trading Prediction in Stock Market, etc. Algorithms to solve those problems are either too specialised or too generalised

Categories of EAs Genetic Algorithms Evolutionary Strategies Evolutionary Programming Genetic Programming More similarities than differences

Genetic Algorithms In 1950 s, Biologists used computers for biological system simulation. First introduced in 1960 s by John Holland from the University of Michigan Modeling Adaptive Process Designed to solve discrete/integer optimization problem

Genetic Algorithms Operate on Binary Strings, binary as the representation of individuals Applying recombination operator with mutation as background operator

Evolutionary Strategies First developed by Rechenberg in 1973 Solved parameter optimization problems Individuals represented as a pair of float-valued vectors Apply both recombination and self adaptive mutation

Evolutionary Strategies Similar to Genetic Algorithms in recombination and mutation processes Differences with Genetic Algorithms Evolutionary Strategies are better at finding local maximum while Genetic Algorithms are more suitable at finding global maximum Thus, Evolutionary Strategies are faster than Genetic Algorithms Evolutionary Strategies are represented as real number vector while GAs are represented using bitstrings

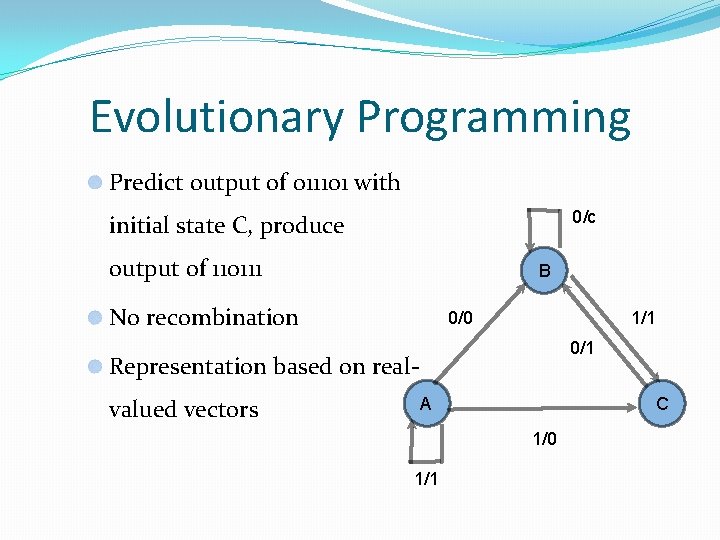
Evolutionary Programming Developed by Lawrence Fogel in 1962 Aimed at evolution of Artificial Intelligence in developing ability to predict changes in environment Use Finite State Machine for prediction

Evolutionary Programming Predict output of 011101 with 0/c initial state C, produce output of 110111 B No recombination 0/0 1/1 0/1 Representation based on realvalued vectors A C 1/0 1/1

Genetic Programming Developed by Koza to allow the program to evolve by itself during the evolution process Individuals are represented by Tree or Graphs

Genetic Programming Different from GA, ES, EP where representation is linear (bit strings and real value vectors), Tree is non-linear Size depend on Depth and Width, while other representations have a fixed size Only requires crossover OR mutation

Mutation Binary Mutation: Flipping the bits, as there are only two states of binary values : 0 and 1 Mutating (0, 1, 0, 0, 1) will produce (1, 0, 1)

Mutation Real Value Mutation: Randomly created value added to the variables with some predefined mutation rate Mutation rate and Mutation step need to be defined Mutation rate is inversely proportional to the number of variables (dimensions)

Sources & References Eiben A. E 2004, “What is Evolutionary Algorithm”, Available from: <http: //www. cs. vu. nl/~gusz/ecbook/Eiben. Smith-Intro 2 EC-Ch 2. pdf>. [29 August 2012 ]. Michalewicz, Z. , Hinterding, R. , and Michalewicz, M. , Evolutionary Algorithms, Chapter 2 in Fuzzy Evolutionary Computation, W. Pedrycz (editor), Kluwer Academic, 1997. T. Bäck, U. Hammel, and H. -P. Schwefel, “Evolutionary computation: comments on the history and current state”, IEEE Transactions on Evolutionary Computation 1(1), 1997 X. Yao, “Evolutionary computation: a gentle introduction”, Evolutionary Optimization, 2002 Whitley, D 2001, “An Overview of Evolutionary Algorithm: Practical Issues and Common Pitfalls”, Information and Software Technology, vol. 43, pp. 817 -831

Self Adaptation �Don’t know what values to assign to parameters – so let them evolve! �Population consisting of real vectors x = (x 1, x 2, …, xn) �We produce offspring by adding random vectors to them

Step Size �Schwefel (1981): add vectors whose components are Gaussian random variates with mean 0 �What standard deviation should be used? �The standard deviation evolves as the algorithm is running

Step Size �Represent entities as (x, s) – the individual itself (x) and a step vector (s) �We start by producing an offspring s’ from s: si’ = si exp(cn-1/2 N(0, 1) + dn-1/4 Ni(0, 1)) n = generation number, c, d>0 constants �We produce an offspring x’ from x: xi’ = xi + si’Ni(0, 1)

Self Adaptation �Other parameters can evolve using similar ideas �Sources: Bäck T, Hammel, U & Schwefel, H-P 1997, ‘Evolutionary computation: comments on the history and current state’, IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 3 -17. Available from: IEEE Xplore Digital Library [23 rd August 2012]. Beyer, HG 1995, ‘Toward a Theory of Evolution Strategies: Self. Adaptation’, Evolutionary Computation, vol. 3, no. 3, pp. 311 -348. Saravanan, N, Fogel, DB & Nelson, KM 1995, ‘A comparison of methods for self-adaptation in evolutionary algorithms’, Bio. Systems, vol. 36, no. 2, pp. 157 -166. Available from: Science Direct [26 th August 2012]. Schwefel, H-P 1981, Numerical Optimization of Computer Models, Wiley, Chichester.

Recombination �Produce offspring from 2 or more entities in the original population �Most easily addressed using bitstring representations

One Point Crossover �Entities are represented in the population as bitstrings of length n �Randomly select a crossover point p from 1 to n (inclusive) �Take the substring formed by the first p bits of the first string and append to it the last n-p bits of the second string to give offspring

One Point Crossover �Bitstrings of length 8: 01011100 and 00001111 �Choose crossover point of 6 �Take the first 6 bits from 01011100 �Take the last 2 bits from 00001111 �Form the offspring 01011111

Uniform Crossover �Form a new offspring from 2 parents by selecting bits from each parent with a particular probability �For example, given strings: 11001011 and 0101 �Select bits from the first string with probability ½

Uniform Crossover �Rolled a die 8 times: 2, 3, 6, 6, 3, 1, 3, 5 �Whenever the result is 3 or less, take a bit from the first string, otherwise, take a bit from the second string: 23663135 11001011 and 0101 �Produce offspring: 11011011

Other Variants �Multiple crossover points �Multiple parents �Probabilistic application �Source: Bäck T, Hammel, U & Schwefel, H-P 1997, ‘Evolutionary computation: comments on the history and current state’, IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 3 -17. Available from: IEEE Xplore Digital Library [23 rd August 2012].

Selection �How individuals and their offspring from one generation are selected to fill the next generation �May be probabilistic or deterministic

Proportional Selection �Probabilistic method �Assume that fitness f(x)>0 for every entity x in the population �p(y) = f(y) / (sum of f(x) for every x)

Tournament Selection �Probabilistic method �Select q individuals randomly from the population with uniform probability �The best individual of this set goes into the next generation �Repeat until the next generation is filled

(μ, λ)-Selection �Deterministic method �From a generation of μ individuals, λ>μ offspring are produced �The next generation is produced from the μ fittest individuals of the λ offspring �The fittest member of the next generation may not be as fit as the fittest member of the previous generation

(μ+λ)-Selection �Deterministic method �From a generation of μ individuals, λ offspring are produced �The next generation is produced from the μ fittest individuals from the μ+λ parents and offspring �The fittest members will always survive

Selection �Best method (or methods) will be problem specific �Sources: Bäck T 1994, ‘Selective pressure in evolutionary algorithms: a characterization of selection mechanisms’, Proceedings of the First IEEE Conference on Evolutionary Computation, pp. 57 -62. Available from: IEEE Xplore Digital Library [28 th August 2012]. Bäck T, Hammel, U & Schwefel, H-P 1997, ‘Evolutionary computation: comments on the history and current state’, IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 3 -17. Available from: IEEE Xplore Digital Library [23 rd August 2012].

Travelling Salesman Problem (TSP) �Travelling salesman problem: �This is a hard problem (NP-hard, "at least as hard as the hardest problems in NP") �The DP solution is O(n 2. 2 n) �Genes are a sequence representing the order that the cities are visited in �Example: [0 5 3 4 8 2 1 6 7 9]

Crossover in TSP �A possible crossover: The greedy crossover. �"Greedy crossover selects the first city of one parent, compares the cities leaving that city in both parents, and chooses the closer one to extend the tour. If one city has already appeared in the tour, we choose the other city. If both cities have already appeared, we randomly select a non-selected city. " � Sources: � J. J. Grefenstetts, R. Gopal, B. Rosmaita, and D. Van Gucht. Genetic Algorithms for the Traveling Salesman problem. In Proceedings of an International Conference on Genetic Algorithms and Their Applications, pages 160– 168, 1985.

Mutation in TSP �A possible mutation: The greedy-swap. �"The basic idea of greedy-swap is to randomly select two cities from one chromosome and swap them if the new (swapped) tour length is shorter than the old one" �Sources: �S. J. Louis, R. Tang. Interactive Genetic Algorithms for the Travelling Salesman Problem. Genetic Adaptive Systems Lab, University of Neveda, Reno. 1999.

Applications �EAs are a very powerful computational tool �EAs find application in: �bioinformatics �phylogenetics �computational science �engineering �economics �chemistry �manufacturing �mathematics �physics and other fields

Applications �Computer-automated design �Automotive design � � Design composite materials and aerodynamic shapes to provide faster, lighter, more fuel efficient and safer vehicles No need to spend time in labs working with models �Engineering design � Optimise the design of many tools/components ie. turbines

Applications �Game playing �Sequence of actions can be learnt to win a game �Encryption and code breaking �Telecommunications �DP problems: �Travelling salesman problem � Plan for efficient routes and scheduling for travel planners. �Knapsack problem

Sources T. Bäck, U. Hammel, and H. -P. Schwefel, “Evolutionary computation: comments on the history and current state”, IEEE Transactions on Evolutionary Computation 1(1), 1997 X. Yao, “Evolutionary computation: a gentle introduction”, Evolutionary Optimization, 2002