Evolution Strategies A Tutorial Complete Yiming Objectives For

Evolution Strategies A Tutorial (Complete) Yiming

Objectives • For newly-coming students • • For senior students • • Get familiar with EC techniques Get inspired with some design principles in ES For myself • Learn from all of audiences

Outline • Where • What • How • When/Why

Where • All fields of optimisation including continuous, discrete, combinatorial, with or without constraints • The objective function, i. e. , f(y), can be represented in mathematical form, via simulations, or even in terms of measurements obtained from real objects.

Examples …and more….

When

What • A search paradigm • Inspired by biological evolution • General EC algorithm

Main principles of ES Mating Selection (fitness-independent or fitness-based) Recombination Survivor Selection Mutation and Parameter control

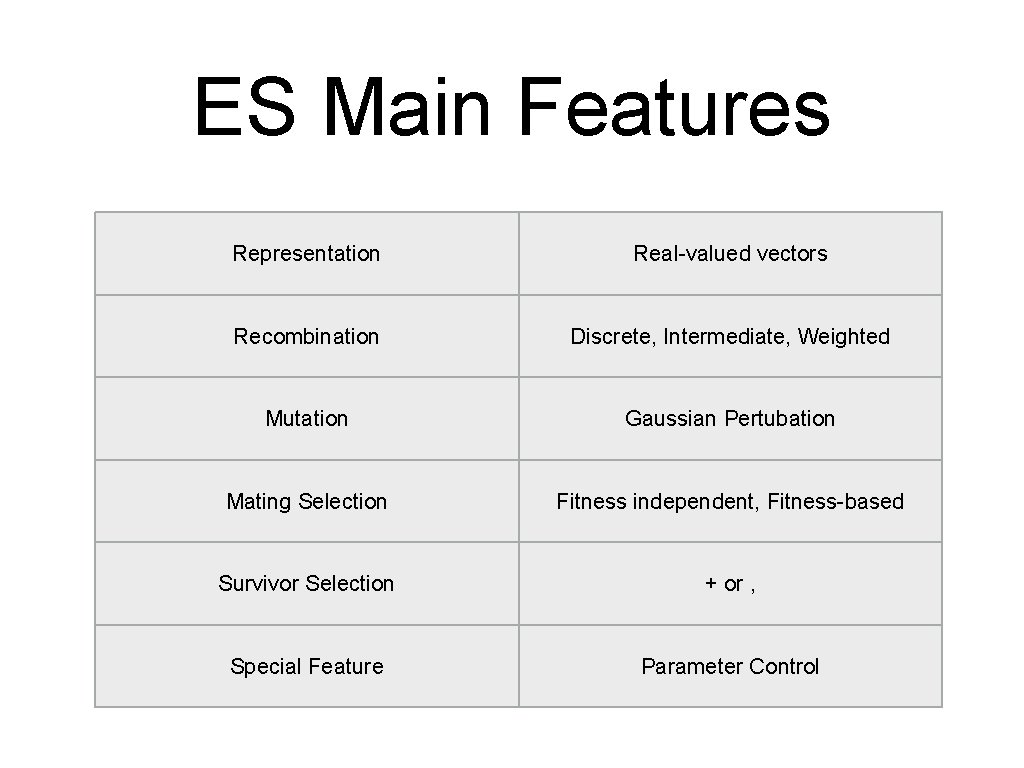
ES Main Features Representation Real-valued vectors Recombination Discrete, Intermediate, Weighted Mutation Gaussian Pertubation Mating Selection Fitness independent, Fitness-based Survivor Selection + or , Special Feature Parameter Control

Notations • —Number of parents are used for recombination • —Number of offspring • —“plus” selection selects the best of considering their ages • — “comma” selection selects the youngest individuals, parents die out • In this case of using comma selection , individuals without must hold.

Two Algorithm Templates

Recombination • Recombination combines information from several parents to generate a single new offspring • Discrete (Dominant) • • Intermediate • • Weighted average of values from all selected parents Others • • Average values of values from all selected parents Weighted • • Uniform select one parent to inherit values One-point and two-point crossover, etc. Note: ES allows multi-combination ( rho > 2)

Mutation • Mutation introduces (“small”) variations by adding a point symmetric perturbation to the result of recombination. • The perturbation is drawn from a multivariate normal distribution, We have • Spherical/isotropic (Uncorrelated) • • with step size Axis-parallel (Uncorrelated) • • General (Correlated) .

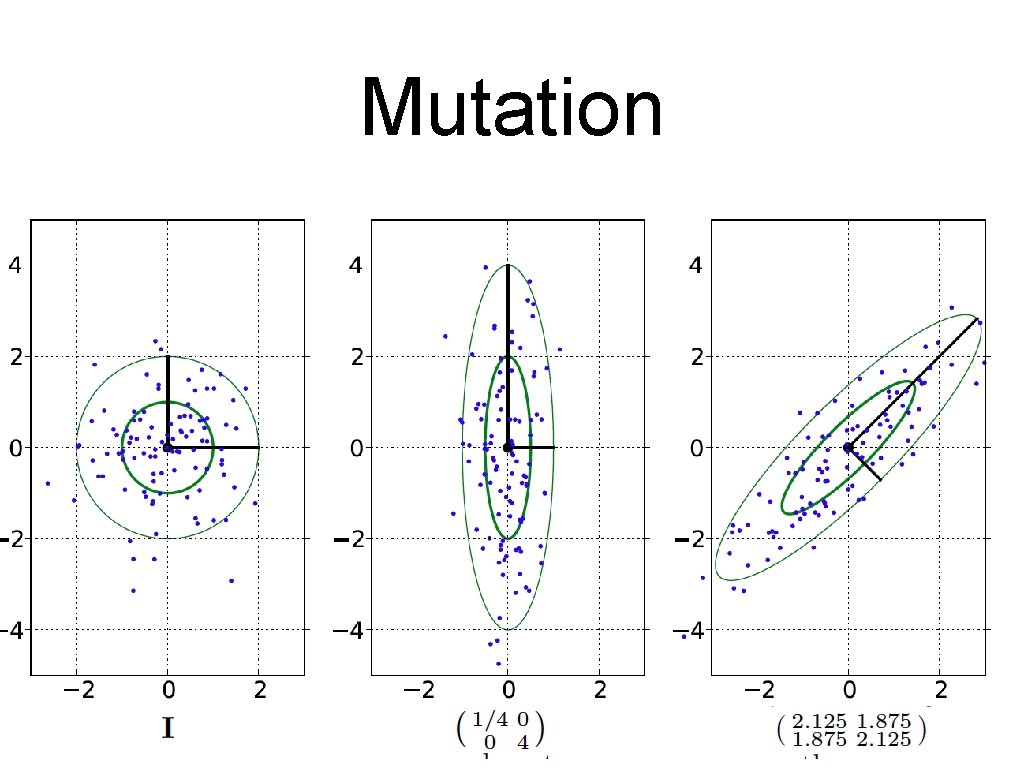
Mutation

Parameter Control • The key of ES • Goal: drive the endogenous strategy parameters (e. g. , step-size) close to their optimal values.

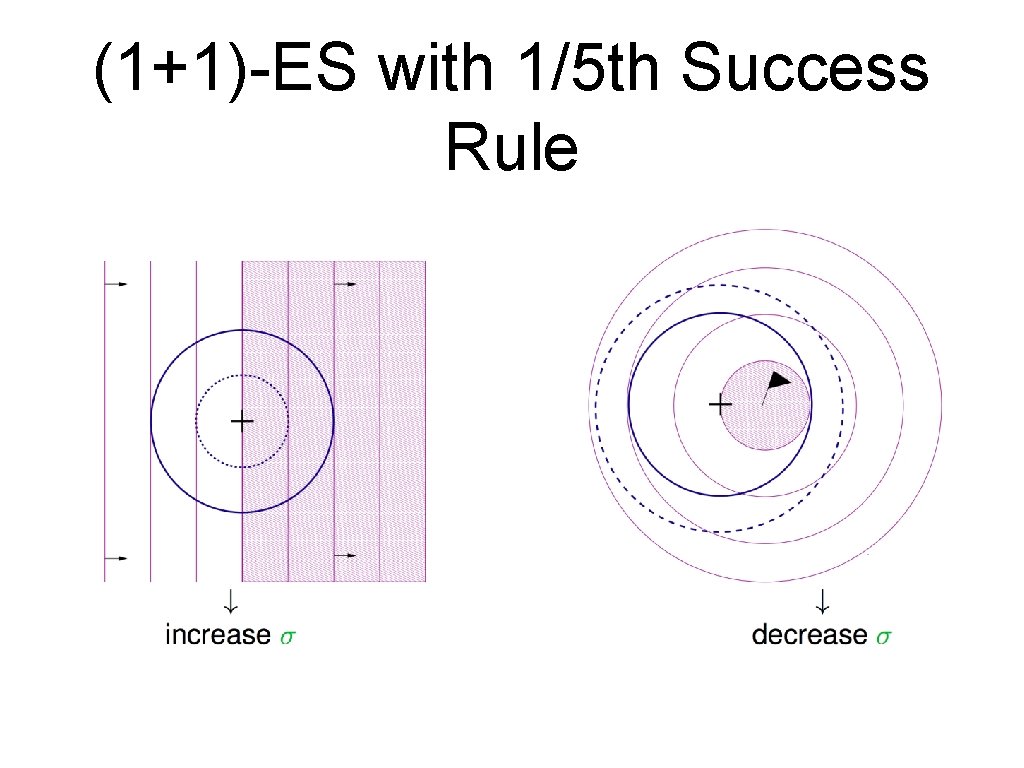
(1+1)-ES with 1/5 th Success Rule

Sigma is IMPORTANT • Principle: Increasing it when the successful rate is high, decreasing it when the successful rate is low. • Other ways to adapt it via evolution • Self-adaptation • Derandomized Self-adaptation • Non-local derandomized step-size control

Address Dependencies CMA-ES

Natural Evolutionary Strategy

Examples • 1+1 ES (1/5 rules) • u+u ES • NES

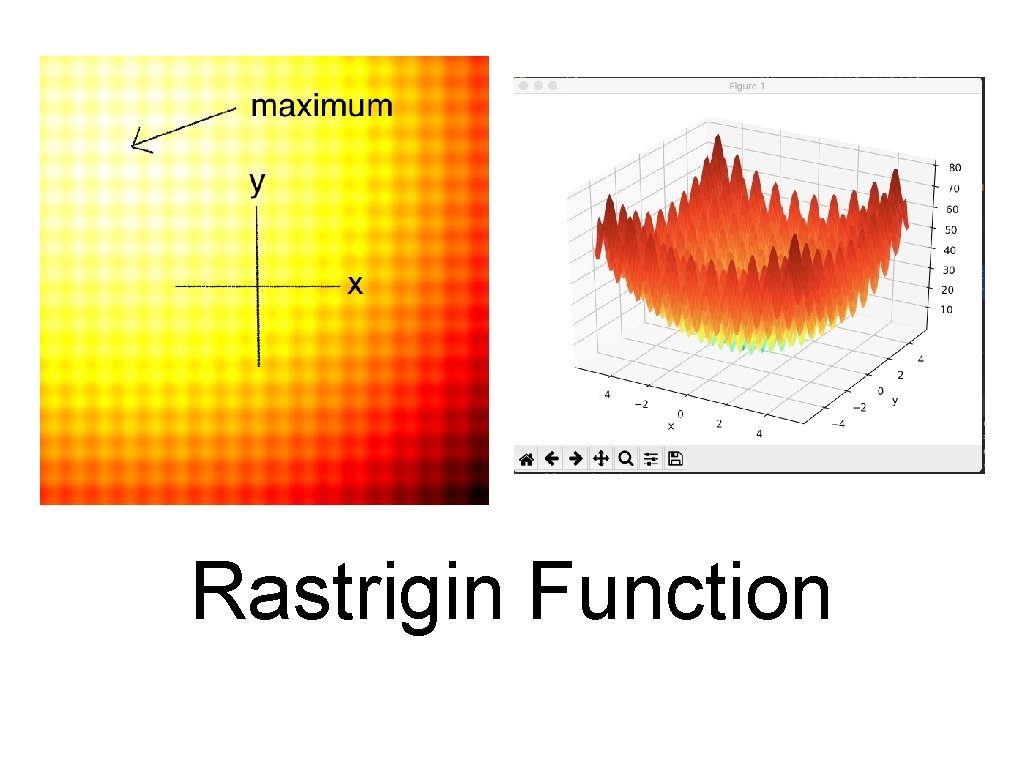
Rastrigin Function

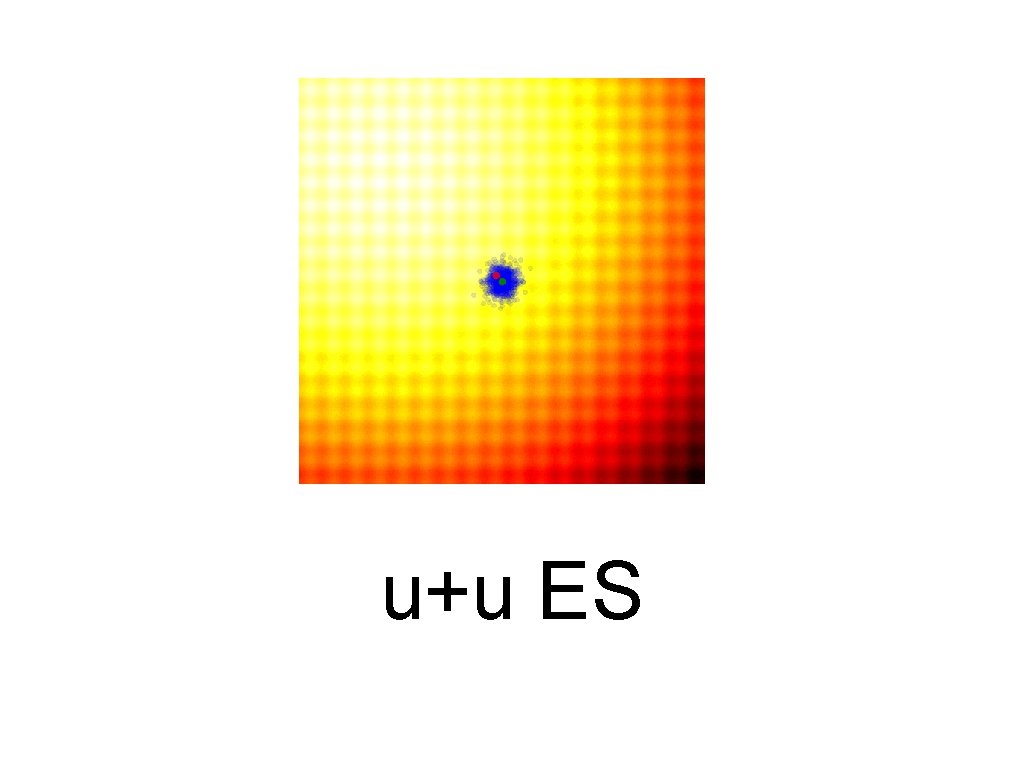
u+u ES

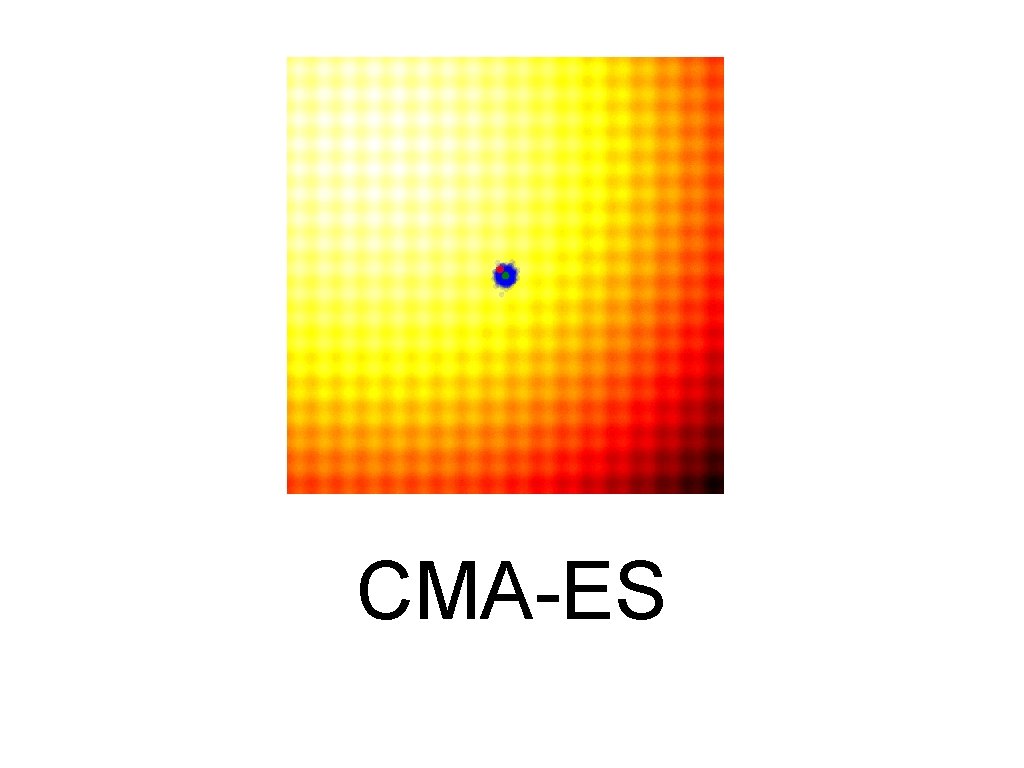
CMA-ES

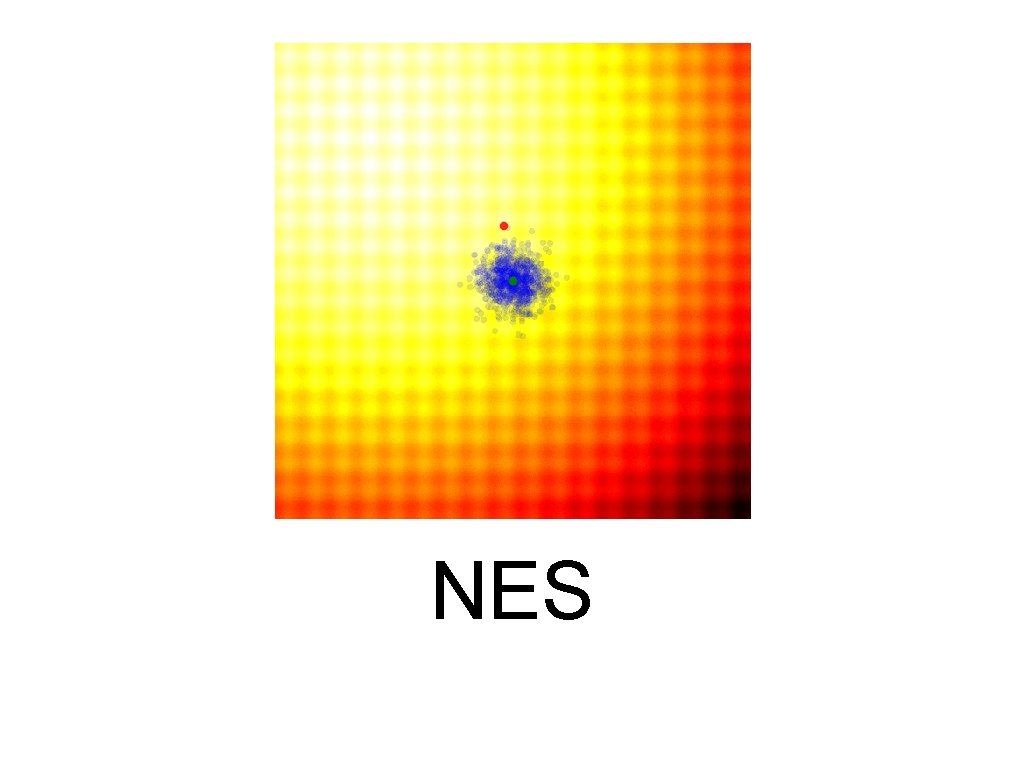
NES

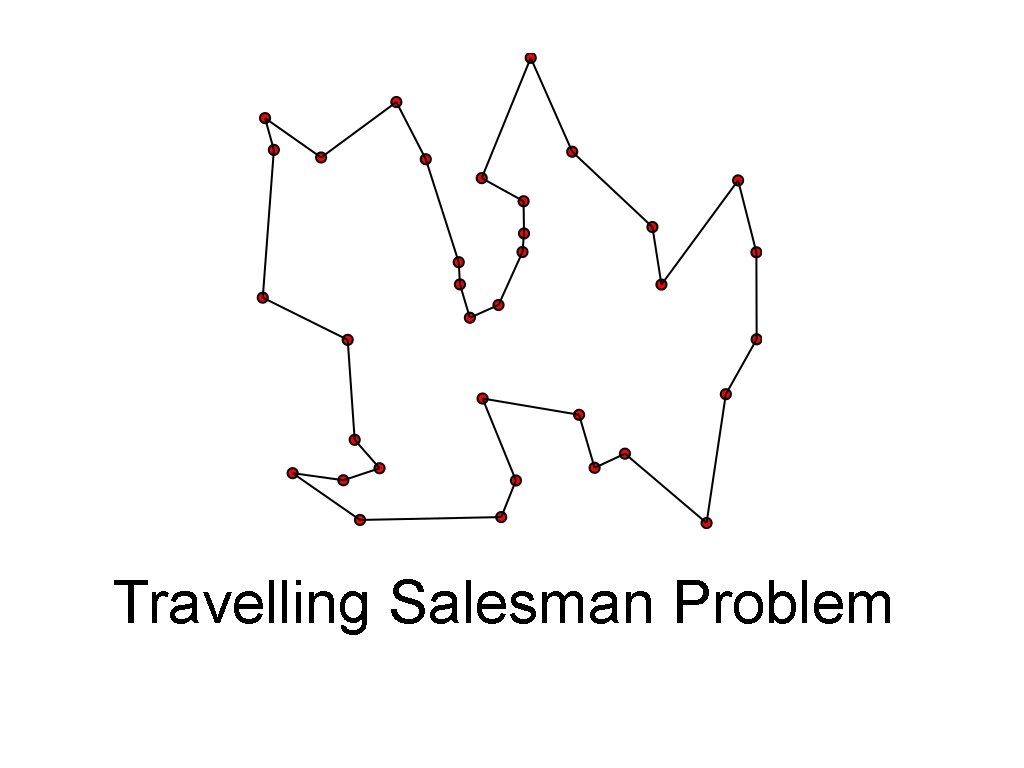
Travelling Salesman Problem

How do you solve the TSP problem?

Some possible ways • Mathematical Programming - Google OR-tools • • Memetic algorithms • • Lin, S. (1965). Computer solutions of the traveling salesman problem. The Bell system technical journal, 44(10), 2245 -2269. Ant colony algorithms • • https: //developers. google. com/optimization/routing/tsp https: //github. com/ppoffice/ant-colony-tsp Simulated Annealing • https: //github. com/ildoonet/simulated-annealing-for-tsp

• Genetic Algorithms • • • Many can be found, I also implemented one. Neural Networks • https: //github. com/jpowie 01/TSP-NN-Training • http: //jamestunnell. github. io/blog/2014/06/09/chaotictsp/ And many more

Can this optimisation problem be solved by learning?

What about Deep Learning?

Some possible ways • Deep Supervised learning • • ? Deep Reinforcement learning • https: //github. com/pemami 4911/neural-combinatorial-rlpytorch • https: //multithreaded. stitchfix. com/blog/2016/07/21/skyn et-salesman/

Skynet Salesman

CNN plays a game

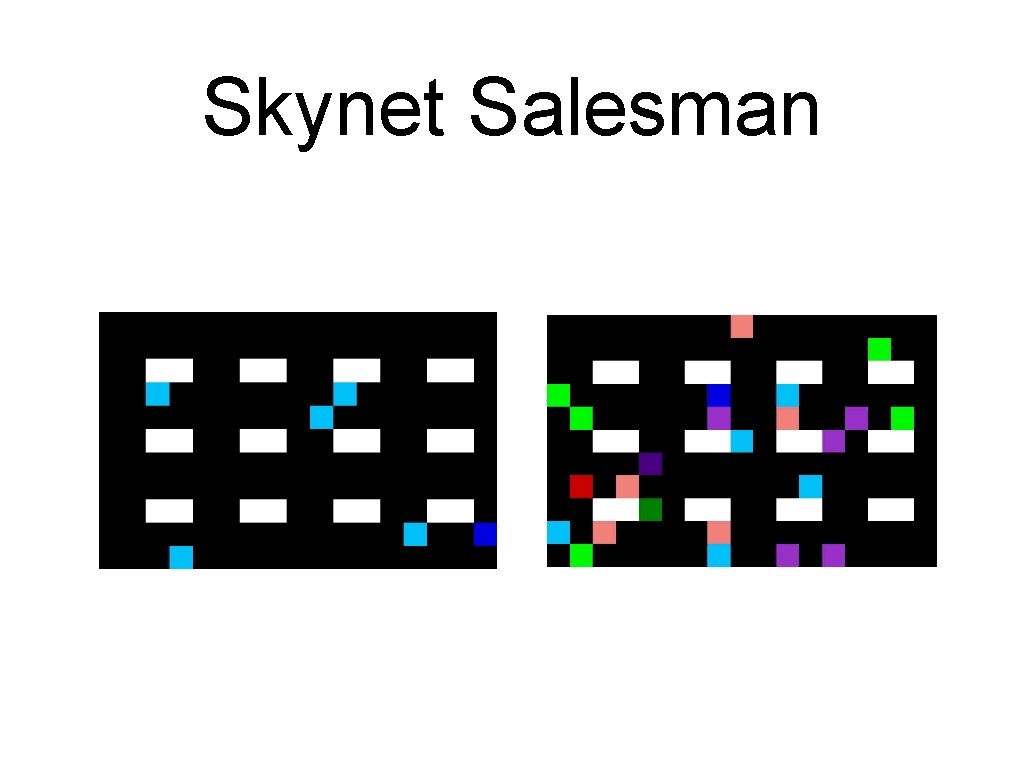
Skynet Salesman

Can we expand this idea to other combinatorial optimisation problems?