Evolution models competition Lectures III George Kampis ETSU








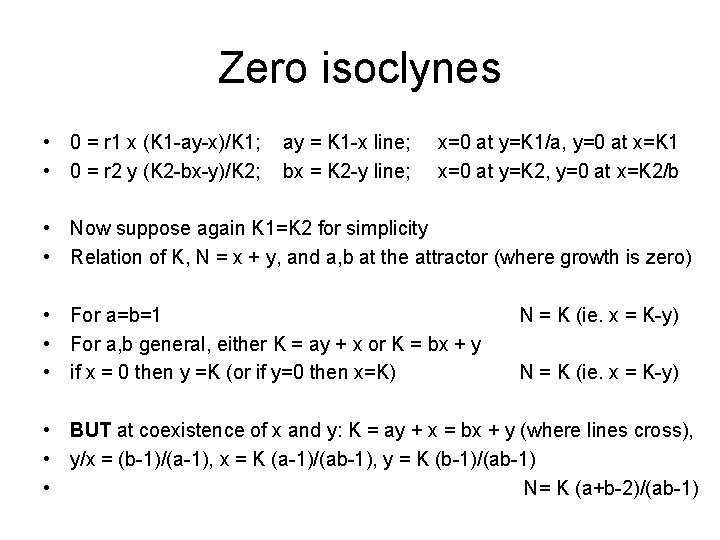
















- Slides: 34

Evolution models: competition Lectures I-II George Kampis ETSU 2007 Spring

Lecture I: Verhulst and LV

Evolution • Darwin: natural selection = differential survival/repr. • Selection (competition) dynamics • GA • • Malthus: population growth Verhulst growth equation Lotka-Volterra competition equations Hypercompetition • Coming together: selection, competition, dynamics, complex systems modeling

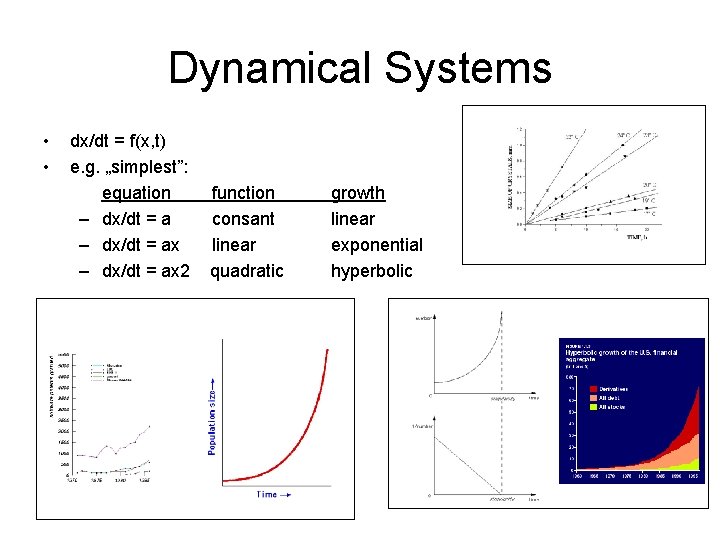
Dynamical Systems • • dx/dt = f(x, t) e. g. „simplest”: equation – dx/dt = ax 2 function consant linear quadratic growth linear exponential hyperbolic

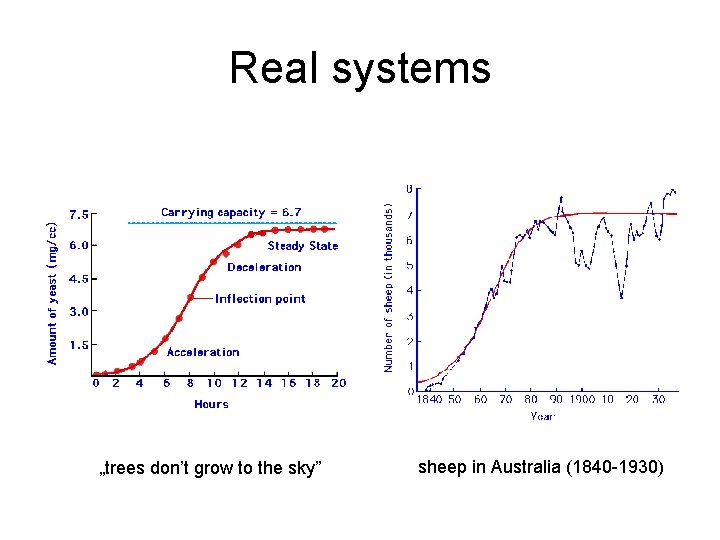
Real systems „trees don’t grow to the sky” sheep in Australia (1840 -1930)

Selection is. . • • • Differential reproduction Not all offspring can survive … … or reproduce Derived concept: fitness This together with mutation and crossover defines classic evolution (and GA)

Verhulst equation • dx/dt = rx , r = „Malthusian parameter” • dx/dt = rx (K-x)/K , K = limit intraspecies competition (density dep. ) „logistic equation”, generates S-shape see inset • Effect of r and K? see inset, interactive simulation

Lotka-Volterra competion • dx/dt = r 1 (K-y-x)/K x • dy/dt = r 2 (K-x-y)/K y intraspecies competition (for K) with interspecies coupling • interspecies competition coefficient (how much room occupied). . • dx/dt = r 1 (K-ay-x) x • dx/dt = r 2 (K-bx-y) y

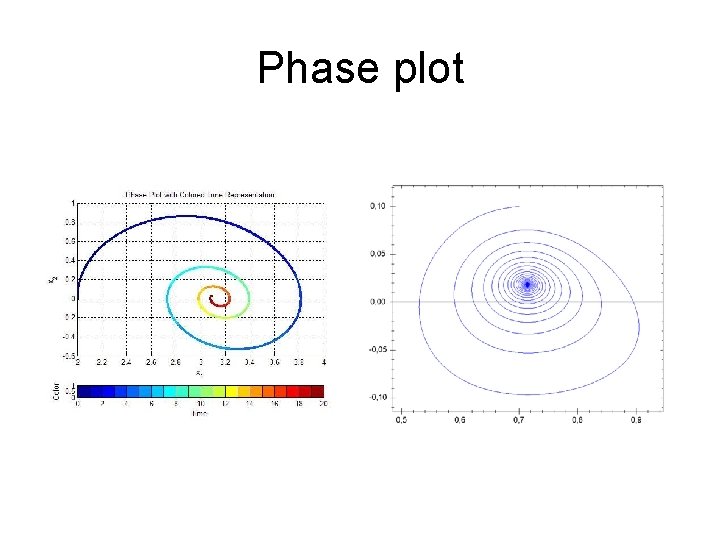
Phase plot

Phase plot concepts • Trajectories, attractors, stability – fixed points, limit cyles, etc.

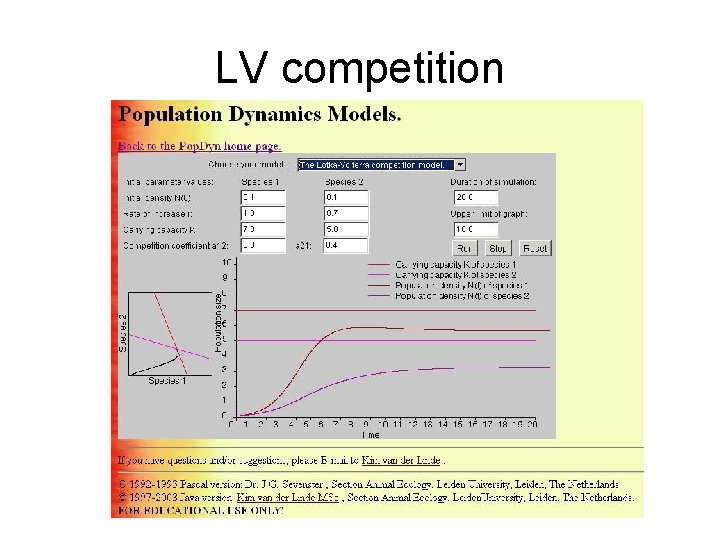
LV competition

Lotka-Volterra comp. (reminder) • dx/dt = r 1 x (K-y-x)/K • dy/dt = r 2 y (K-x-y)/K intraspecies competition (for the K) with interspecies coupling • interspecies competition coefficient (how much room occupied). . • dx/dt = r 1 x (K-ay-x)/K • dx/dt = r 2 y (K-bx-y)/K • Effect of various K-s for populations, e. g. efficiency (small vs. big) • dx/dt = r 1 x (K 1 -ay-x)/K 1 • dx/dt = r 2 y (K 2 -bx-y)/K 2

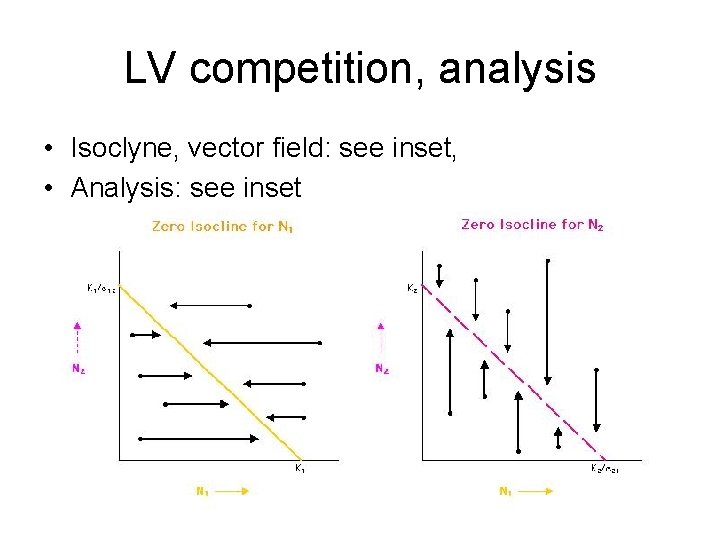
LV competition, analysis • Isoclyne, vector field: see inset, • Analysis: see inset
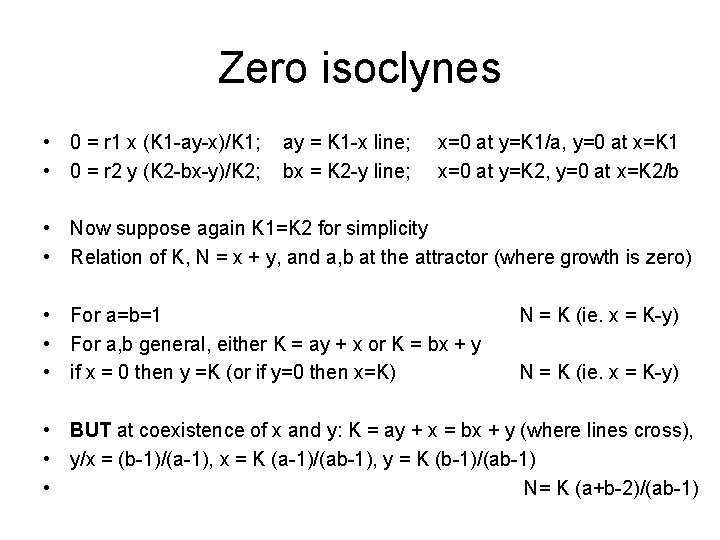
Zero isoclynes • 0 = r 1 x (K 1 -ay-x)/K 1; • 0 = r 2 y (K 2 -bx-y)/K 2; ay = K 1 -x line; bx = K 2 -y line; x=0 at y=K 1/a, y=0 at x=K 1 x=0 at y=K 2, y=0 at x=K 2/b • Now suppose again K 1=K 2 for simplicity • Relation of K, N = x + y, and a, b at the attractor (where growth is zero) • For a=b=1 • For a, b general, either K = ay + x or K = bx + y • if x = 0 then y =K (or if y=0 then x=K) N = K (ie. x = K-y) • BUT at coexistence of x and y: K = ay + x = bx + y (where lines cross), • y/x = (b-1)/(a-1), x = K (a-1)/(ab-1), y = K (b-1)/(ab-1) • N= K (a+b-2)/(ab-1)

Cexistence cont’d • If the x and y population coexist, this can be where the lines cross, which in turn can be anywhere on the plane (bw 0, 0 and K, K), depending on the values of a and b. So N = x+ y can be anything bw 0 and 2 K. • The geometric meaning of N: the coinciding "natural" K lines at 45 degrees mark the "baseline" case N=K. For a, b >1 their cross point moves downwards, for a, b < 1 upwards, pushing N=x+y above or below the baseline, i. e. N above (or below) K.

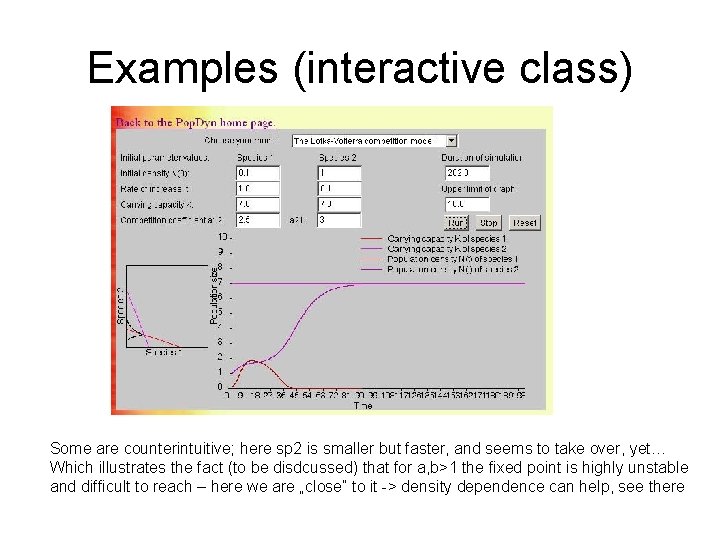
Examples (interactive class) Some are counterintuitive; here sp 2 is smaller but faster, and seems to take over, yet… Which illustrates the fact (to be disdcussed) that for a, b>1 the fixed point is highly unstable and difficult to reach – here we are „close” to it -> density dependence can help, see there

Coexistence vs selection in LVc • Coexistence at common points of K lines • Because these are the only points, where dx/dt = 0 AND dy/dt =0 • So unless the two lines coincide (!), • coexistence is at the cross point, if there is one (!) • Role of (x 0, y 0) and (r 1, r 2): determine if this point on the phase plane is actually accessible • For a, b < 1 there is cross, and always accessible • For a, b > 1 there is cross, difficult to access • Sensitive switching behavior (test interactively)

Lessons from LV competition • • • the „big trick” is with the K lines. if they are different, there can be states where species 1 cannot grow but species 2 still has growth reserves (or the way around). so one species will grow and take over the other, no matter what. competition coeff. has similar effects (in reality perhaps K and a, b are related) so there would be one single parameter (eg efficiency) • Malthusian parameter has (often) no effect! • Initial conditions have (often) no effect! • Many, perhaps most (realistic) combinations yield coexistence!!
Lecture II: Hyperbolic growth

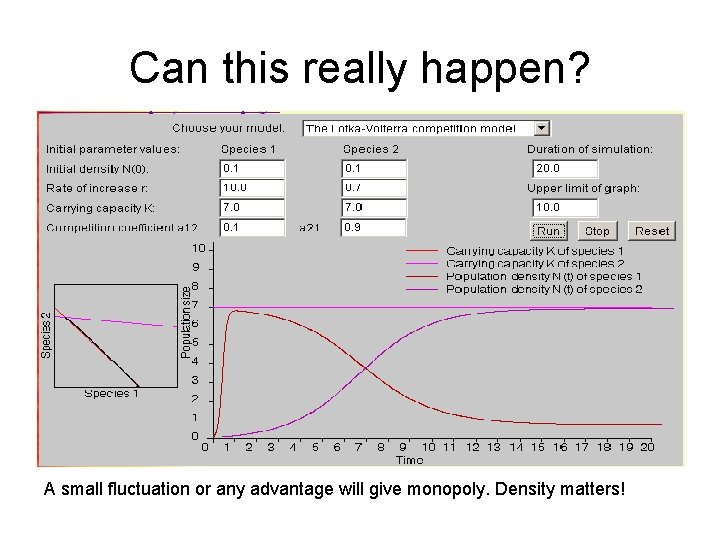
Can this really happen? A small fluctuation or any advantage will give monopoly. Density matters!

Hyperbolic competition • Hypercycle • (Eigen 1971) Explanation of terms!

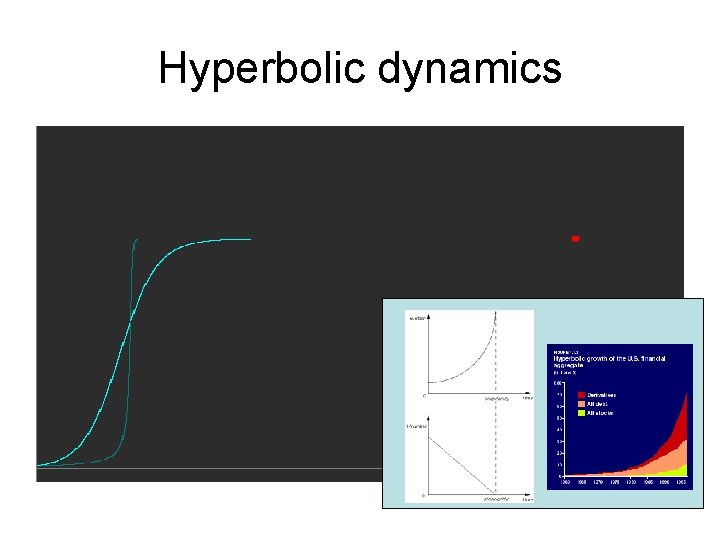
Hyperbolic dynamics

Spatial effects of hyperbolic dynamics • Tree growth, crystal growth, etc.

Voronoi polygons A polygon whose interior consists of all points in the plane which are closer to a particular lattice point than to any other. The generalization to dimensions is called a Dirichlet region, Thiessen polytope, or Voronoi cell.

Voronoi, nonlin. growth examples

Voronoi, different examples (!) Descartes 1644 Hay, beecomb… etc. http: //www. igg. tu-berlin. de/fileadmin/Daten_FMG/Geo. Tech/geoinfo_technology_lect 11. ppt

Applications • Biology, Ecology, Forestry -- Model and analyze plant competition ("Area potentially available to a tree", "Plant polygons") • Cartography -- Piece together satellite photographs into large "mosaic" maps • Crystallography and Chemistry -- Study chemical properties of metallic sodium ("Wigner-Seitz regions");

The temporal dynamics of nonlinear growth • • • Once-and for all selection Frozen accidents (QWERTY phenomenon) Path dependence „first come first served”, „winner takes all” „founder effect” etc.

Path dependence • Not (!) just state dependence (i. e. the past matters) • But order of events, especially initial events have an amplified, persistent effect • Path = order of events • Testable by – Counterfactuals – Random models

Pólya urn model A special case of „balls-and-bins” http: //www-stat. stanford. edu/%7 Esusan/surprise/Polya. html Important: urns, balls, restaurants etc. are all equivalent in this model! And yet…

Fancy words to summarize • Unpredictability: whatever leads to whatever else, fluctuations drive outcomes • Inflexibility: the deeper into, the more rigid • Nonergodicity: small changes dont cancel out each other – Def or ergodicity: temporal and statistical averages coincide • Potential inefficiency: better candidates cant take over after an initial period – Similar to ESS, evolutionary stable strategy

Hyperbolic selection • • Brian Arthur, Michael Mitzenmacher: „law of increasing returns” Theory of monopoly • • But: it is not the growth phase that selects! In that phase everybody grows as can Limited organization (market) effects cause selection as in Verhulst and LV • • Thus, to achieve selection (ie extinction) we need the minus terms too… …which will eliminate the less abundant that produces the more loss Note that the losses are distributed proportionally in this model So, „proportional is not proportional” • • Unless loss is quadratic too, higher numbers win A small advantage becomes a big advantage

Hyperbolic (non)selection

Conclusions • Evolutionary dynamics is often counterintuitive • Selection may be difficult to achieve when you think • Outcome usually depends on factors other than Malthusian parameter is a poor predictor of success Intial population value is a good predictor of success • Question 1: [how] can these factors be grasped in an agent based model (ie. is there a reality behind the equations? ) • Question 2: if any of the above is true [under realistic conditions] then how can evolution happen, i. e. how can small new populations win over?