Evidence synthesis of competing interventions when there is

Evidence synthesis of competing interventions when there is inconsistency in how effectiveness outcomes are measured across studies Nicola Cooper Centre for Biostatistics and Genetic Epidemiology, Department of Health Sciences, University of Leicester, UK. http: //www. hs. le. ac. uk/group/bge/ Acknowledgements: Tony Ades, Guobing Lu, Alex Sutton & Nicky

MULTIPLE EVENT OUTCOMES • Often the main clinical outcome differs across trials § Inconsistent reporting (e. g. mean, median) § Change in outcomes used over time • Possible to use the available data to inform the estimation of others

EXAMPLE: Anti-viral for influenza • Three antiviral treatments for influenza • Amantadine • Oseltamivir • Zanamivir • No direct comparisons of the different antiviral treatments • All trials compare antiviral to standard care • Different outcome measures • Time to alleviation of fever • Time to alleviation of ALL symptoms • Different summary statistics reported • Median time to event • Mean time to event

DATA AVAILABLE • Oseltamivir and Zanamivir trials report median time to event of interest • Amantadine trials report mean time to event of interest • No direct comparison trials of all antivirals & standard care. Important to preserve within-trial randomised treatment comparison of each trial whilst combining all available comparisons between treatments (i. e. maintain randomisation).

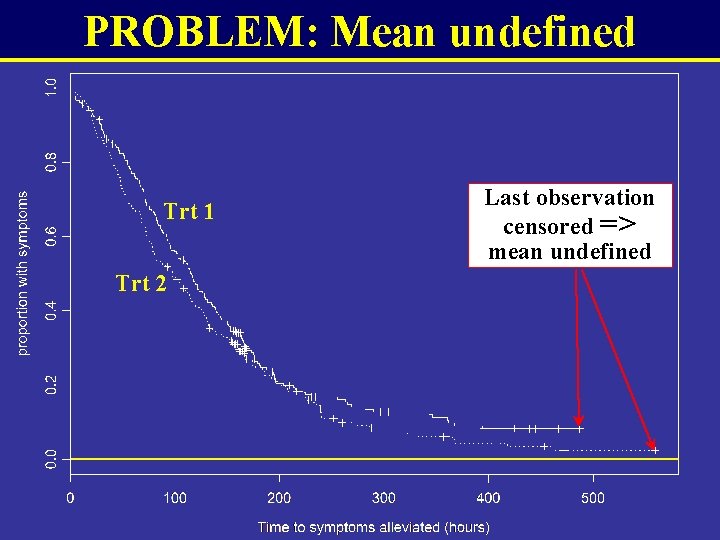
BACKGROUND • In clinical studies with time to event data as the principal outcome, median time to event usually reported. • However, for economic evaluations the statistic of interest is the mean => Area under survival curve (i. e. provides best estimate of expected time to an event) • Often mean time to an event can. NOT be determined from observed data alone due to right -censoring (i. e. actual time to an event for some individuals unknown either due to loss of follow-up or event not

PROBLEM: Mean undefined Trt 1 Trt 2 Last observation censored => mean undefined

CALCULATING MEAN FROM MEDIAN TIME • Simplest approach is to assume an Exponential distribution for time with influenza, thus assuming a constant hazard function over time, • Probability of still having influenza at time t, • At median time, • Mean time to event = 1/ & its corresponding variance = 1/ 2 r, where r = number of events incurred during the study period

THREE STATE MARKOV MODEL 1 2 1 = transition rate (hazard) from influenza onset to alleviation of fever 2 = transition rate from alleviation of fever to alleviation of symptoms 1/ 1 = expected time from influenza onset to alleviation of fever 1/ 2 = expected time from alleviation of fever to alleviation of symptoms (1/ 1 + 1/ 2) = expected time from influenza onset to alleviation of symptoms

EVIDENCE SYNTHESIS MODEL ln( i 1) = j + jk = -ln( 1) # i 1, flu to fev alleviated ln( i 2) = j + jk = -ln( 2) # i 2, fev to sym alleviated i 3 = i 1 + i 2 = 1/ 1 + 1/ 2 # i 3, flu to sym alleviated jk ~ Normal(dk , 2) # log hazard ratio j ~ Normal(g , Vg) # random effect where i = trial arms, j = trials, k = treatments. Prior distributions specified for dk , g , 2, Vg Assumptions: • Equal treatment effects in each period, jk • Baseline hazard during second period same as in first period plus an additional random effect term, j

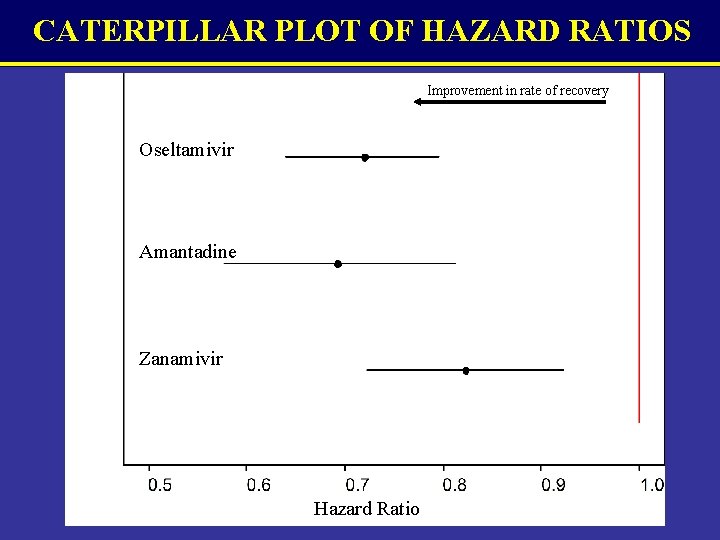
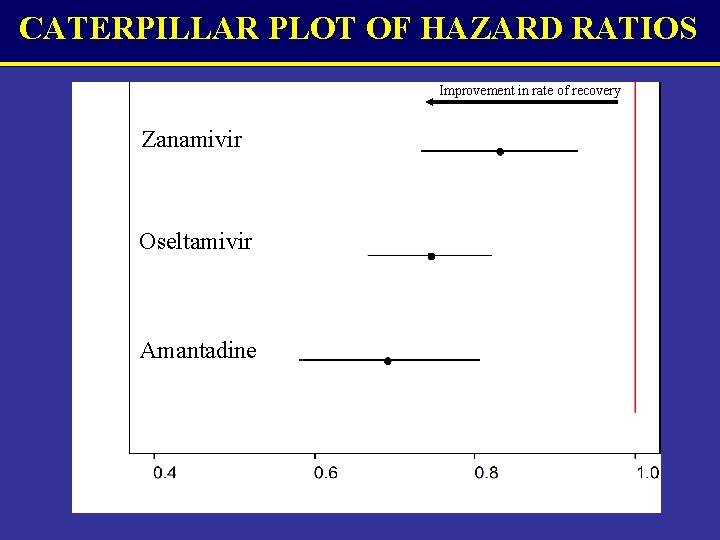
HAZARD RATIO / RELATIVE HAZARD Exp(dk) is the ratio of hazards of recovery at any time for an individual on treatment k relative to an individual on the standard treatment If exp(dk) < 1 then treatment k is superior If exp(dk) > 1 then standard treatment is superior Model fitted in Win. BUGS and evaluated using MCMC simulation

CATERPILLAR PLOT OF HAZARD RATIOS Improvement in rate of recovery Oseltamivir Amantadine Zanamivir Hazard Ratio

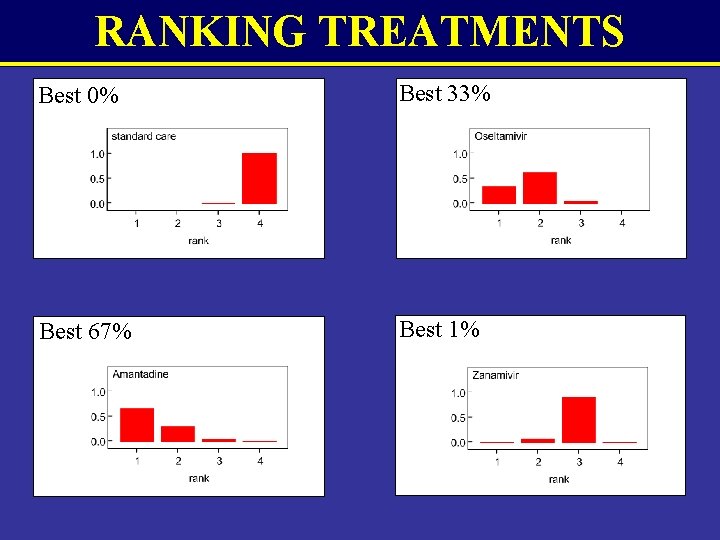
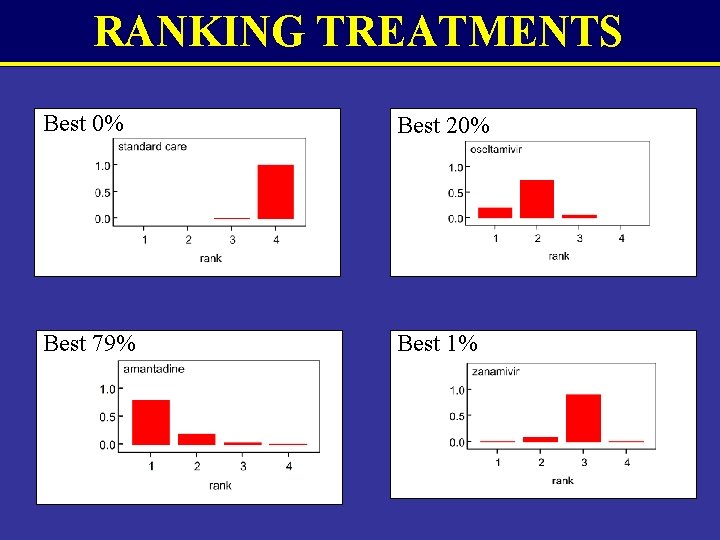
RANKING TREATMENTS Best 0% Best 33% Best 67% Best 1%

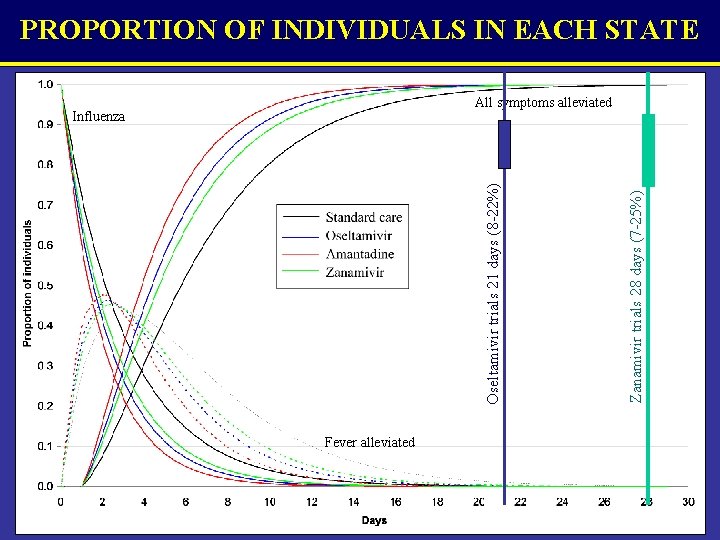
PROPORTION OF INDIVIDUALS IN EACH STATE Oseltamivir trials 21 days (8 -22%) Influenza Fever alleviated Zanamivir trials 28 days (7 -25%) All symptoms alleviated

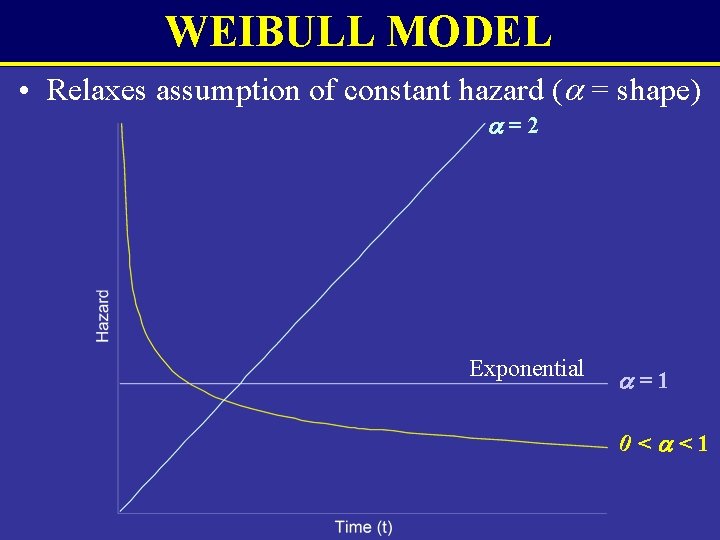
WEIBULL MODEL • Relaxes assumption of constant hazard ( = shape) =2 Exponential =1 0< <1

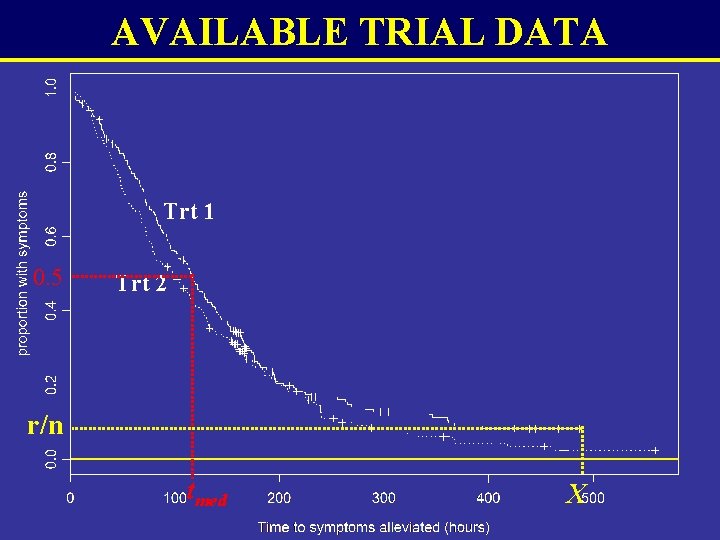
WEIBULL MODEL (cont. ) • Probability of still having influenza at time t, S(t)=e -(t/ ) >0 (shape) >0 (scale) -(tmed/ ) tmed= (ln(2))1/ • At median time, 0. 5=e • If r out of n individuals still had symptoms at X days (i. e. end of trial), the proportion of censored individuals can be expressed as: S(t(X)) =r/n=e -(t/ )

AVAILABLE TRIAL DATA Trt 1 0. 5 Trt 2 r/n tmed X

WEIBULL MODEL (cont. ) • Important to calculate E(S(t(X))|tmed) to take account of the correlation between median time (tmed) to alleviation of illness and proportion of participants (r/n) still at X days as they are from the same trial dataset. • Mean time to event (i. e. statistic of interest) (1+1/ )

EVIDENCE SYNTHESIS MODEL ln( i 1) = j + jk = ln( i 1) + ln( (1+1/ 1)) # i 1, flu to fev alleviated ln( i 2) = j + jk # i 2, fev to sym alleviated i 3 = i 1 + i 2 = i 3 (1+1/ 3) # i 3, flu to sym alleviated jk ~ Normal(dk, 2) # log hazard ratio j ~ Normal(g, Vg) # random effect where i = trial arms, j = trials, k = treatments. Prior distributions specified for dk , g , 2, Vg Assumptions: • Equal treatment effects in each period, jk • Baseline hazard during second period same as in first period plus an additional random effect term, j

EVIDENCE SYNTHESIS MODEL (cont. ) • and are the shape and scale parameters of a Weibull distribution respectively • Model assumes the shape parameters are the same for time to alleviation of fever, 1, regardless of antiviral treatment & similarly for time to alleviation of symptoms, 3 to lack of data, to estimate 1 set equal to 1 (i. e. exponential distribution). Could set constraint to ensure proportion still with fever at X days (i. e. end of trial) proportion still with symptoms • Due

CATERPILLAR PLOT OF HAZARD RATIOS Improvement in rate of recovery Zanamivir Oseltamivir Amantadine

RANKING TREATMENTS Best 0% Best 20% Best 79% Best 1%

CONCLUSIONS • Although amantadine is ranked “best” it does have serious side effects (e. g. gastrointestinal symptoms, central nervous system) which are not taken into account in this analysis • This type of model could inform the effectiveness parameters of a cost effectiveness decision model • Allows multiple outcomes & indirect comparisons to be modelled within a single framework • Appropriate model for nested outcomes (e. g. progressionfree survival & overall survival) • If non-nested outcomes, then a multivariate meta-analysis model, as developed for surrogate outcomes, more appropriate