Evidence in favor of Density Wave Theory 06112019

Evidence in favor of Density Wave Theory 06/11/2019 M. SHAMEER ABDEEN Department of Physics, University of Arkansas, Fayetteville, AR 72701 msabdeen@uark. edu

Density wave theory, originally proposed by C. C. Lin and F. Shu (Lin & Shu 1964), explains the nature of the spiral arm structures in galaxies as density waves that propagates through the galactic disk. The theory predicts the existence of a co-rotation radius and the existence of an age gradient across the spiral arm Figure 1: Propagating spiral arm density waves through the galactic disk and the co-rotation radius Reference: Fei D. , Anderson A. , (2003). Spiral Galaxy Animation. Retrieved Nov 11, 2016, from http: //www 3. amherst. edu/~gsgreenstein/progs/animations/spiral_galaxy/ 2

Finding the co-rotation radius Step 1: De-projecting Galaxies with non-zero inclination angles between the plane of sight and their disks had to be de-projected to a face-on orientation Step 2: Measuring Pitch Angles It is a measurement of how tight the spiral arms are. The measurements were done by two independent methods • 2 DFFT method (Davis et al. 2012) • Spirality (Shields et al. 2016) Figure 2: De-projecting NGC 5194 Table 1: Pitch angle measurements in 3. 6 µm, B-band, 8 µm and FUV-band for the selected 20 galaxies. 3

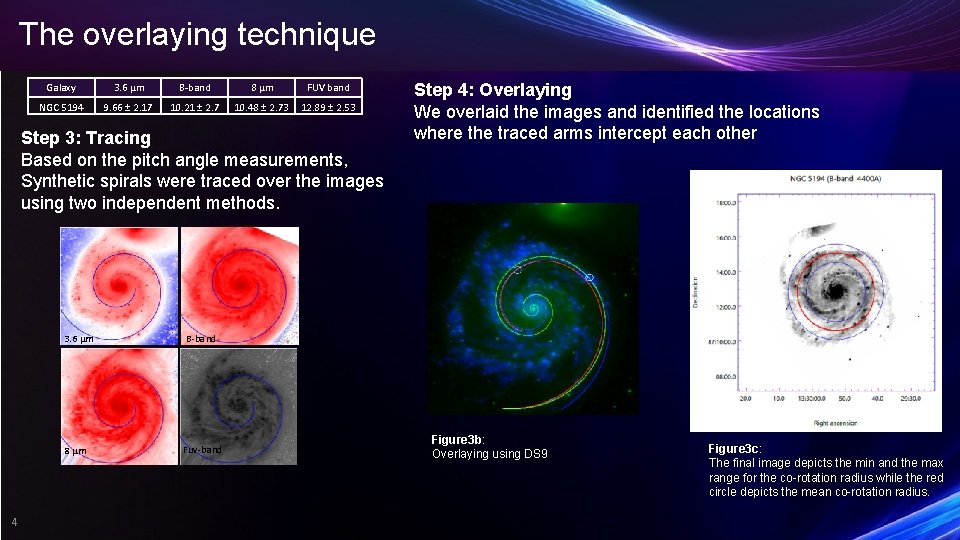
The overlaying technique Galaxy 3. 6 µm B-band 8 µm FUV band NGC 5194 9. 66 ± 2. 17 10. 21 ± 2. 7 10. 48 ± 2. 73 12. 89 ± 2. 53 Step 3: Tracing Based on the pitch angle measurements, Synthetic spirals were traced over the images using two independent methods. 3. 6 µm 8 µm 4 Step 4: Overlaying We overlaid the images and identified the locations where the traced arms intercept each other B-band Fuv-band Figure 3 b: Overlaying using DS 9 Figure 3 c: The final image depicts the min and the max range for the co-rotation radius while the red circle depicts the mean co-rotation radius.

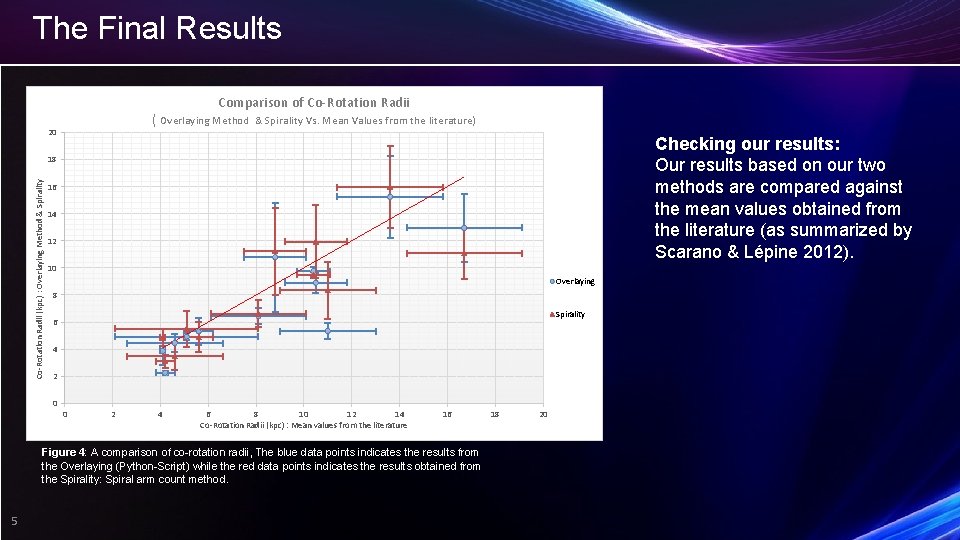
The Final Results Comparison of Co-Rotation Radii ( Overlaying Method 20 & Spirality Vs. Mean Values from the literature) Checking our results: Our results based on our two methods are compared against the mean values obtained from the literature (as summarized by Scarano & Lépine 2012). Co-Rotation Radii (kpc) : Overlaying Method & Spirality 18 16 14 12 10 Overlaying 8 Spirality 6 4 2 0 0 2 4 6 8 10 12 14 Co-Rotation Radii (kpc) : Mean values from the literature 16 Figure 4: A comparison of co-rotation radii, The blue data points indicates the results from the Overlaying (Python-Script) while the red data points indicates the results obtained from the Spirality: Spiral arm count method. 5 18 20

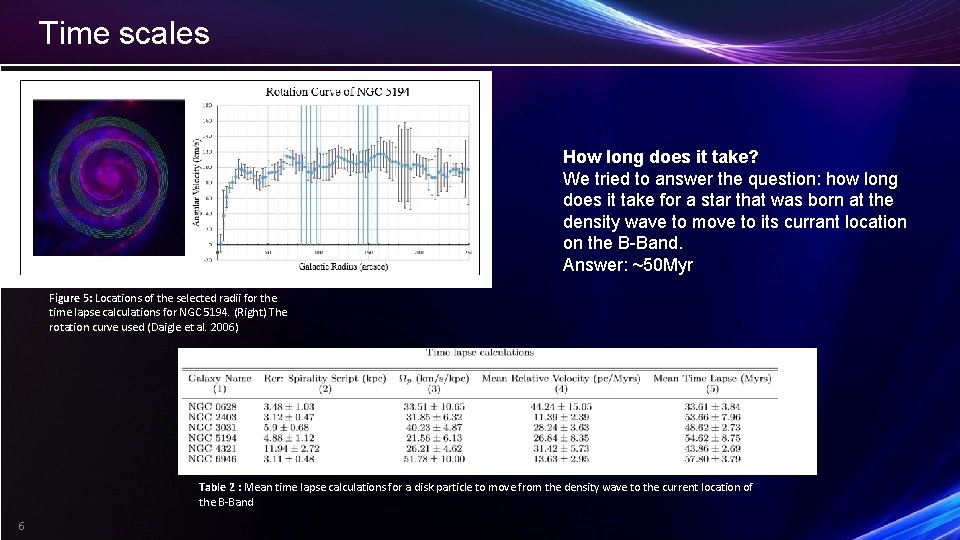
Time scales How long does it take? We tried to answer the question: how long does it take for a star that was born at the density wave to move to its currant location on the B-Band. Answer: ~50 Myr Figure 5: Locations of the selected radii for the time lapse calculations for NGC 5194. (Right) The rotation curve used (Daigle et al. 2006) Table 2 : Mean time lapse calculations for a disk particle to move from the density wave to the current location of the B-Band 6

Summary Why is it important to identify the co-rotation radius: • Since the co-rotation radius has a dynamical influence on the matter and the chemical composition distribution process of the galaxy. Knowing the location, tells us a lot about the galaxy. • The region of stability around the co-rotation radius creates an ideal environment for a Galactic habitable zone (GHZ) e. g. Marochnik (1983); Sundin (2006). Summary: • We have confirmed the validity of Density Wave Theory in a very direct way by using di� erently colored spiral arms to find the co-rotation radius and showing that it agrees well with other methods commonly used. • Although there are considerable amount of uncertainties, the method that we used, is a very simple and a fast method in finding the co-rotation radius • The time scale calculation found that the average time lapse for a star to move from the density wave to the B-band spiral is around 50 Myr, consistent with their being young, recently formed, stars. 7

Thank you M. SHAMEER ABDEEN msabdeen@uark. edu