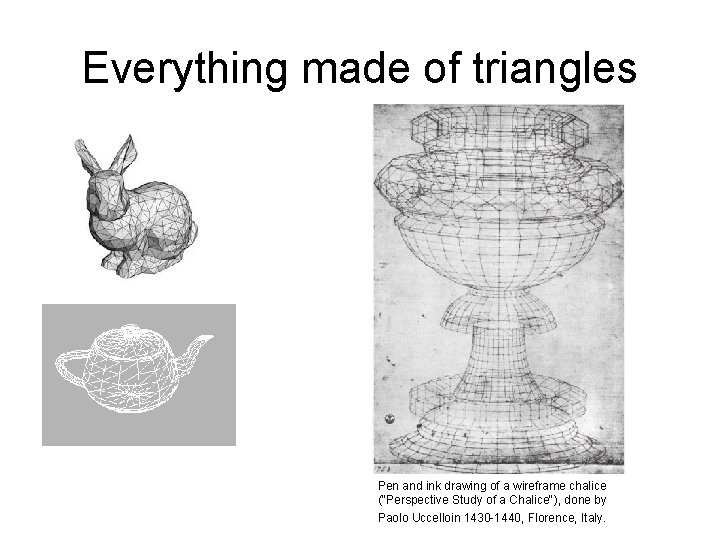
Everything made of triangles Pen and ink drawing

Everything made of triangles Pen and ink drawing of a wireframe chalice ("Perspective Study of a Chalice"), done by Paolo Uccelloin 1430 -1440, Florence, Italy.

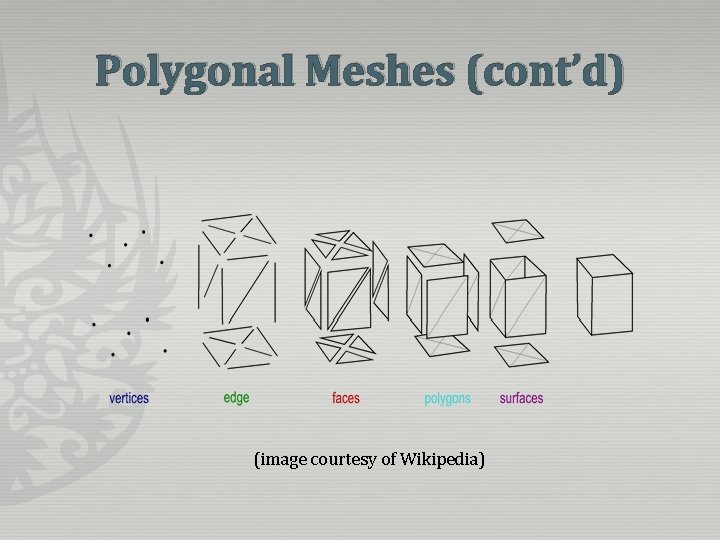
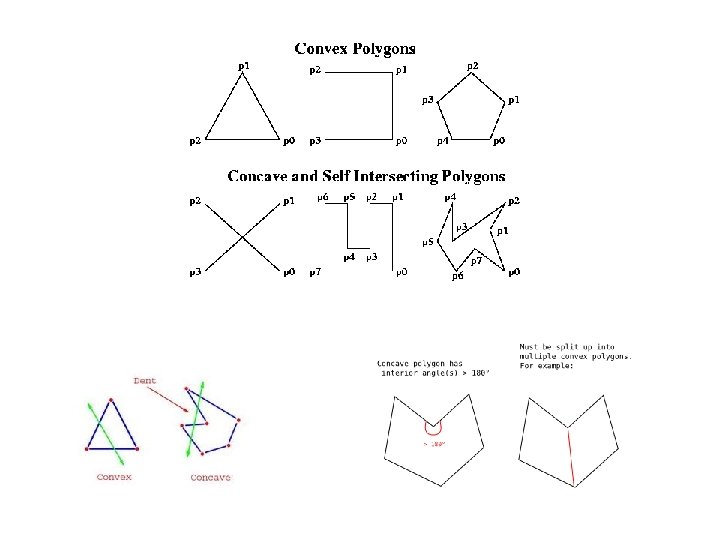
Polygonal Meshes (cont’d) (image courtesy of Wikipedia)

Face-Vertex Meshes (FV) ¢ List of faces defined by vertex indices (image courtesy of Wikipedia)

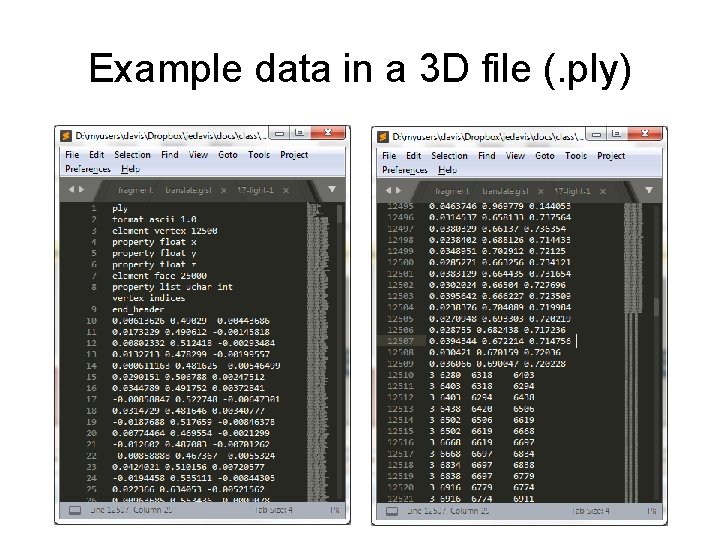
3 D Scene/Model File Formats ¢ ¢ ¢ Wavefront OBJ (. obj) 3 DS Max (. 3 ds) Geomview OFF (Object File Format) (. off) PLY (. ply) for scanned data … and more

Example data in a 3 D file (. ply)

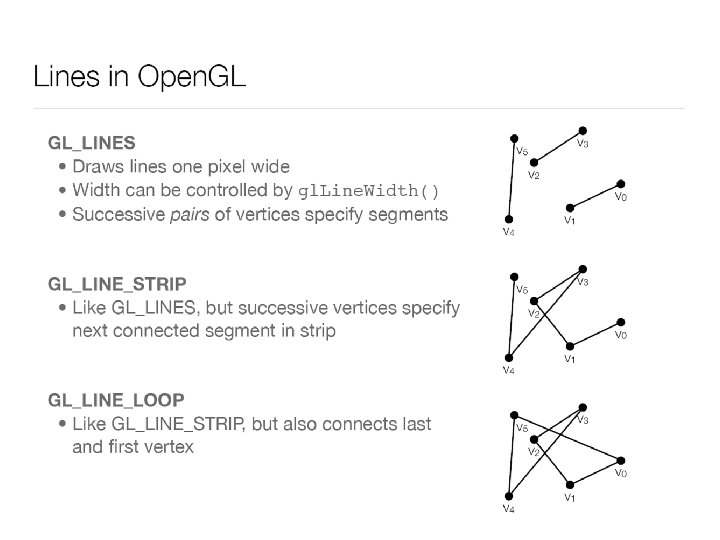
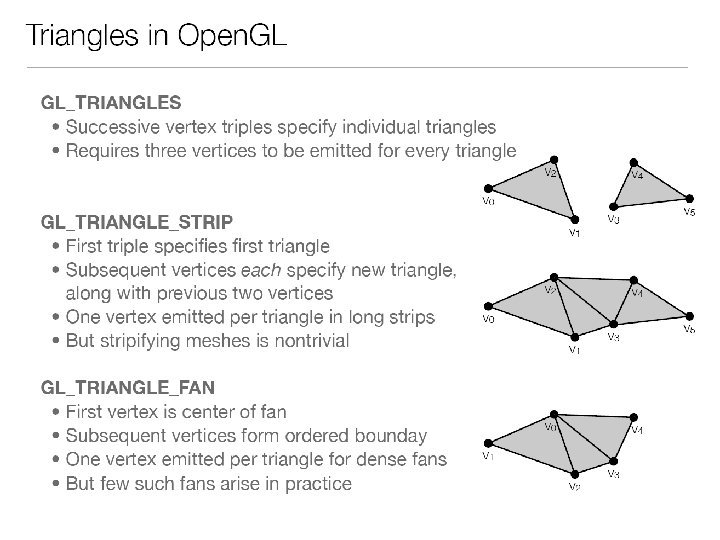
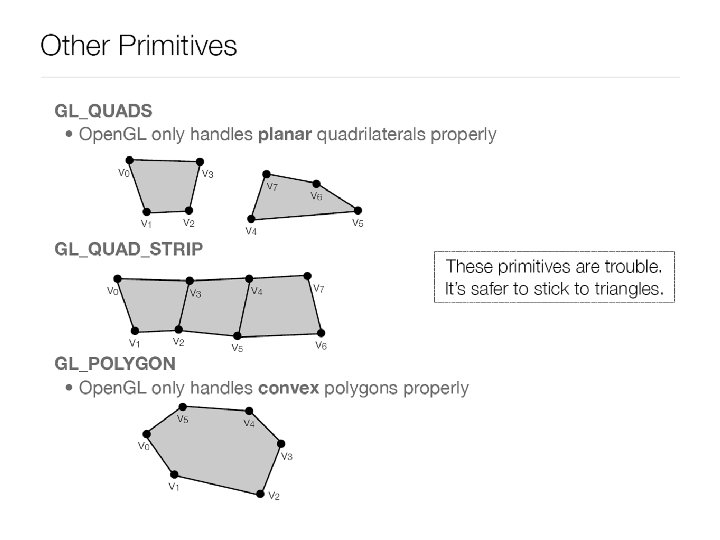
Q: What will render a square? (A) gl. Begin(GL_TRIANGLES) gl. Vertex 3 f(0, 0, 0); gl. Vertex 3 f(1, 1, 0); gl. Vertex 3 f(1, 0, 0); gl. Vertex 3 f(0, 1, 0); gl. Vertex 3 f(1, 1, 0); gl. End(); (C) gl. Begin(GL_TRIANGLES) gl. Vertex 3 f(0, 0, 0); gl. Vertex 3 f(1, 1, 0); gl. Vertex 3 f(1, 0, 0); gl. Vertex 3 f(0, 0, 0); gl. Vertex 3 f(1, 1, 0); gl. Vertex 3 f(0, 1, 0); gl. End(); (B) gl. Begin(GL_QUADS) gl. Vertex 3 f(0, 0, 0); gl. Vertex 3 f(0, 1, 0); gl. Vertex 3 f(1, 0, 0); gl. Vertex 3 f(1, 1, 0); gl. End(); (D) gl. Begin(GL_QUADS) gl. Vertex 3 f(0, 0, 0); gl. Vertex 3 f(0, 1, 0); gl. Vertex 3 f(1, 0, 0); gl. End(); (E) I just really don’t know

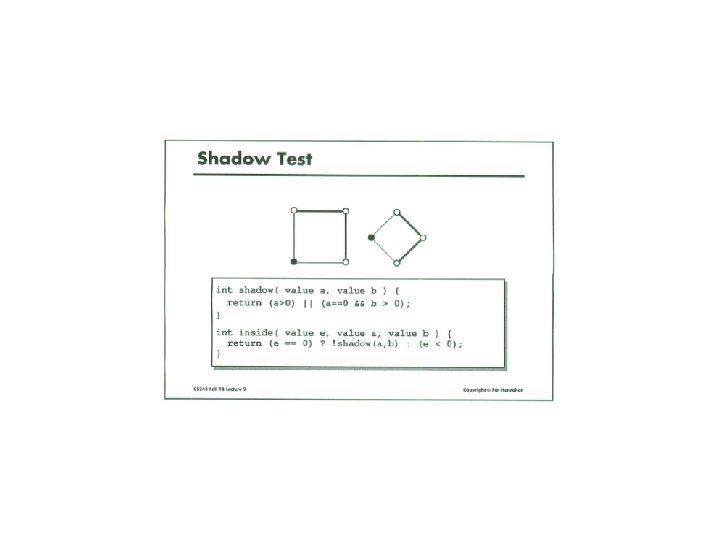
• Turn on all pixels inside the triangle • But what about pixels on the edge?

Top-Left Rasterization Rule [Rasterization Rules (Direct 3 D 10) – MSDN]

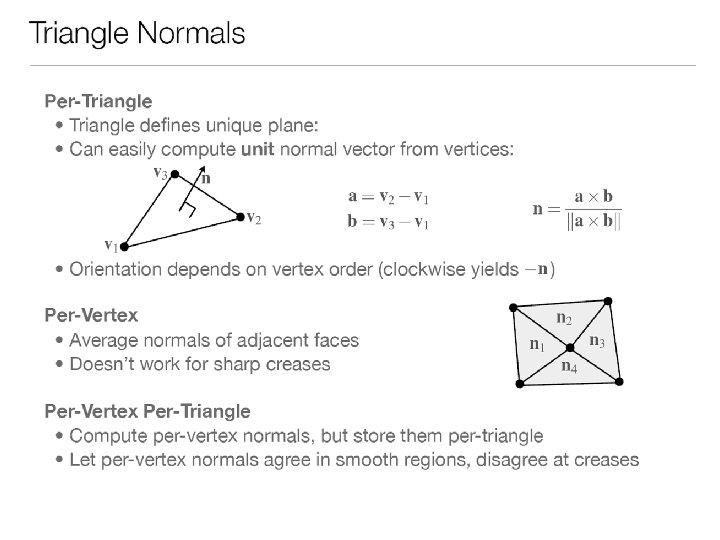
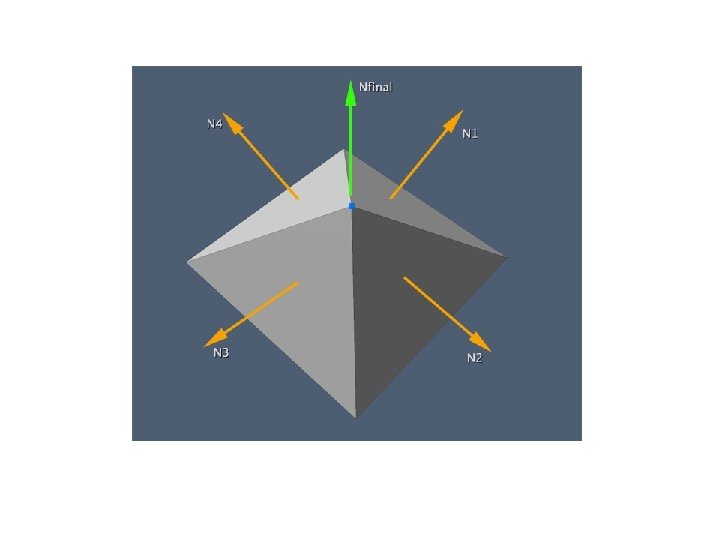
Per vertex vs per face normals

Q about Normals What is the per-polygon normal shown? (A) 1, 1, 1 (B) 0, 0, 1 (C) 1, 0, 0 (D) 0, 1, 0 (E) Don’t know

Q about Normals What is the per-vertex normal at point A? (A) 1, 1, 1 (B) 1, 1, -1 (C) 1/sqrt(3), 1/sqrt(3) (D) -1/sqrt(3), 1/sqrt(3) (E) Don’t know

Limitations of Polygonal Meshes • • Planar facets (& silhouettes) Fixed resolution Deformation is difficult No natural parameterization (for texture mapping) MIT EECS 6. 837, Durand Cutler

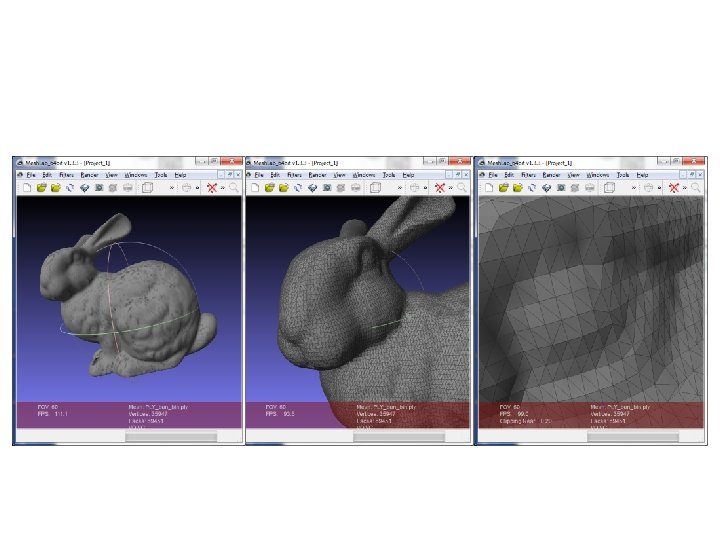
Can We Disguise the Facets? MIT EECS 6. 837, Durand Cutler

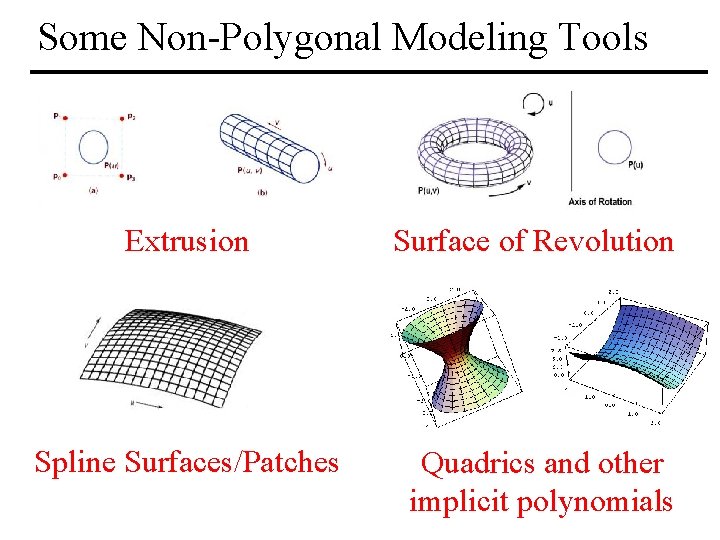
Some Non-Polygonal Modeling Tools Extrusion Surface of Revolution Spline Surfaces/Patches Quadrics and other implicit polynomials MIT EECS 6. 837, Durand Cutler

Continuity definitions: • C 0 continuous – curve/surface has no breaks/gaps/holes • G 1 continuous – tangent at joint has same direction • C 1 continuous – curve/surface derivative is continuous – tangent at join has same direction and magnitude • Cn continuous – curve/surface through nth derivative is continuous – important for shading MIT EECS 6. 837, Durand Cutler

Definition: What's a Spline? • Smooth curve defined by some control points • Moving the control points changes the curve Interpolation Bézier (approximation) BSpline (approximation) MIT EECS 6. 837, Durand Cutler

Interpolation Curves / Splines www. abm. org MIT EECS 6. 837, Durand Cutler

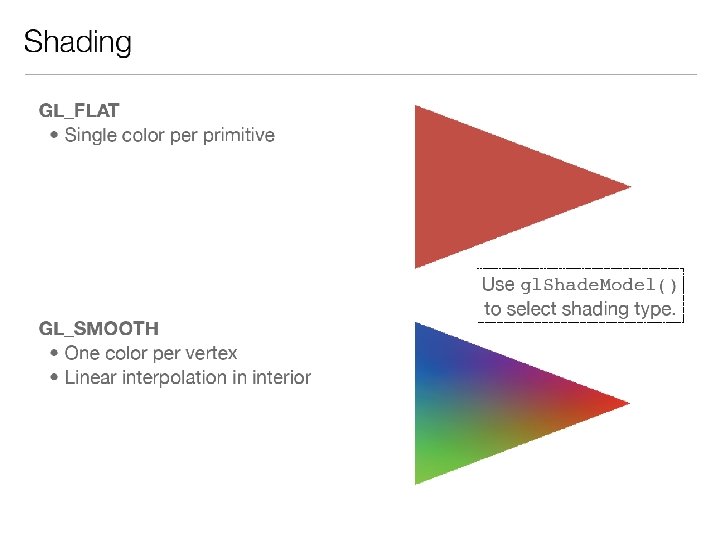
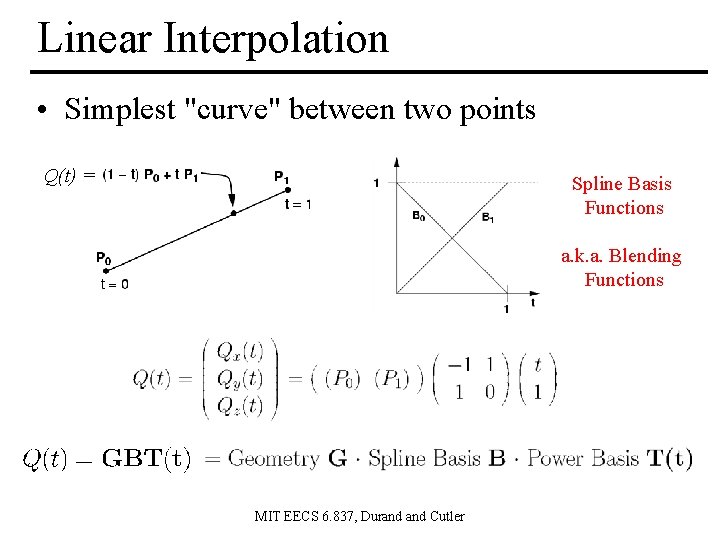
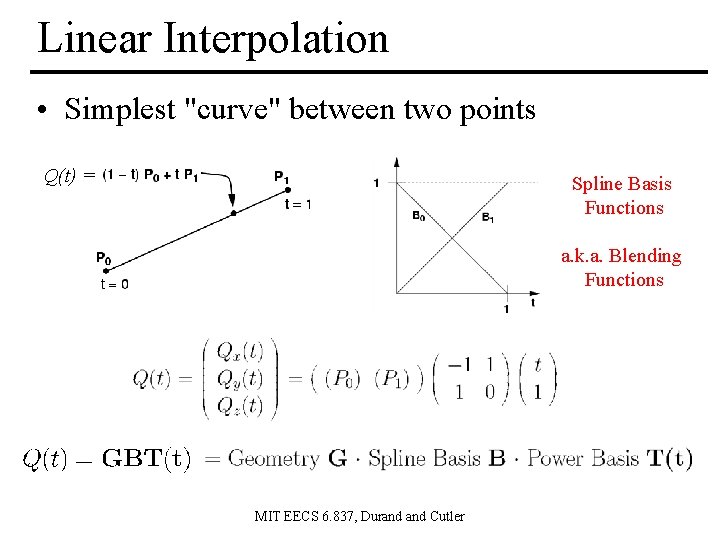
Linear Interpolation • Simplest "curve" between two points Q(t) = Spline Basis Functions a. k. a. Blending Functions MIT EECS 6. 837, Durand Cutler

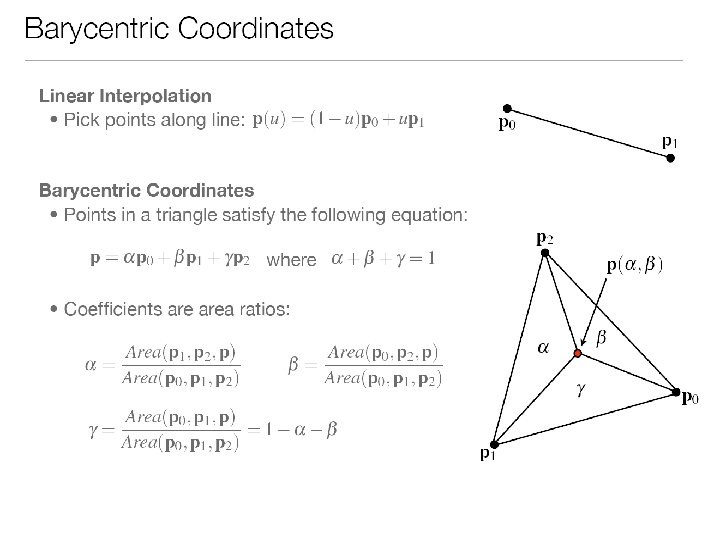
• [bilinear interpolation]

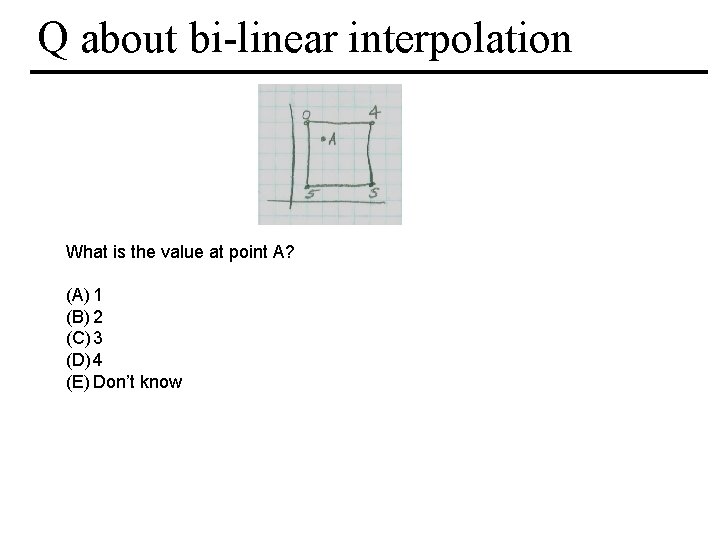
Q about bi-linear interpolation What is the value at point A? (A) 1 (B) 2 (C) 3 (D) 4 (E) Don’t know MIT EECS 6. 837, Durand Cutler

Interpolation is not just about surfaces, used heavily in images Suppose you start with the smallest image and need a big one? MIT EECS 6. 837, Durand Cutler

Nearest, bilinear, b-spline interpolation MIT EECS 6. 837, Durand Cutler

Interpolation vs. Approximation Curves Interpolation Approximation curve must pass through control points curve is influenced by control points MIT EECS 6. 837, Durand Cutler

Interpolation vs. Approximation Curves • Interpolation Curve – over constrained → lots of (undesirable? ) oscillations • Approximation Curve – more reasonable? MIT EECS 6. 837, Durand Cutler

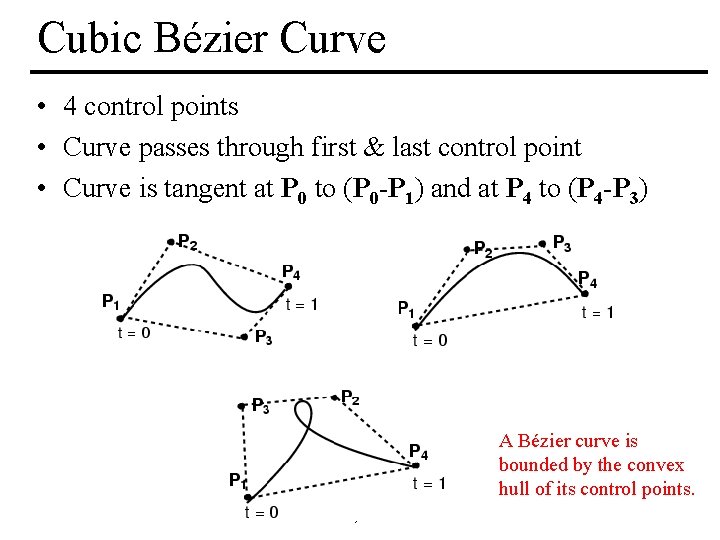
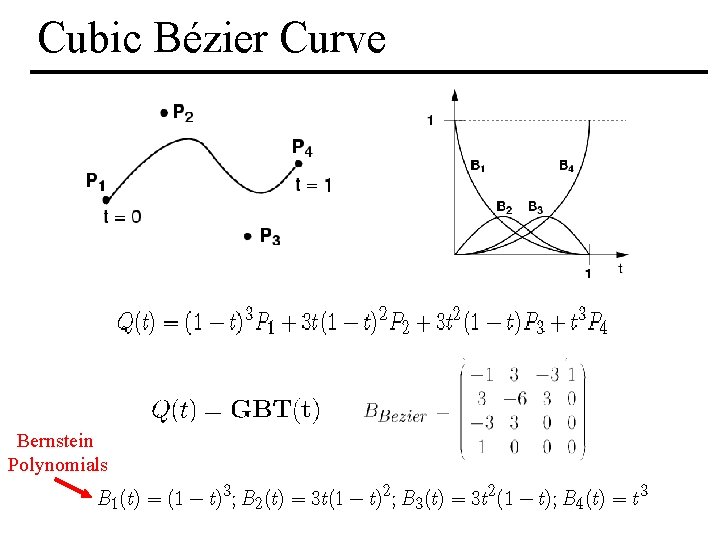
Cubic Bézier Curve • 4 control points • Curve passes through first & last control point • Curve is tangent at P 0 to (P 0 -P 1) and at P 4 to (P 4 -P 3) A Bézier curve is bounded by the convex hull of its control points. MIT EECS 6. 837, Durand Cutler

Linear Interpolation • Simplest "curve" between two points Q(t) = Spline Basis Functions a. k. a. Blending Functions MIT EECS 6. 837, Durand Cutler

Cubic Bézier Curve Bernstein Polynomials MIT EECS 6. 837, Durand Cutler

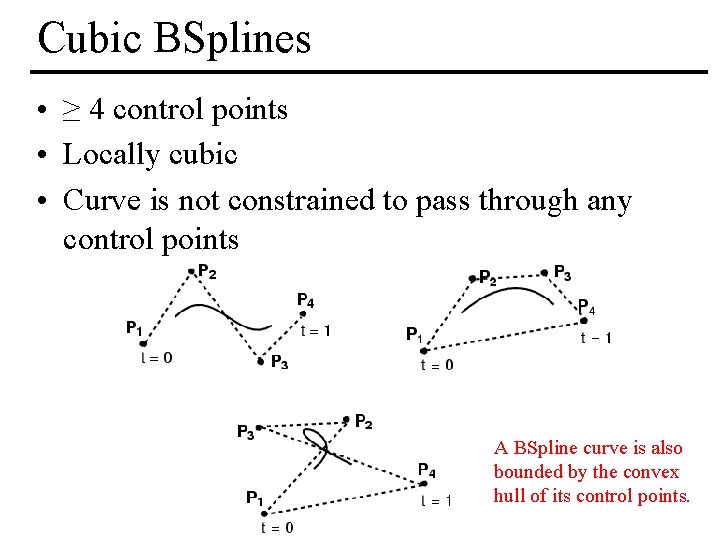
Cubic BSplines • ≥ 4 control points • Locally cubic • Curve is not constrained to pass through any control points A BSpline curve is also bounded by the convex hull of its control points. MIT EECS 6. 837, Durand Cutler

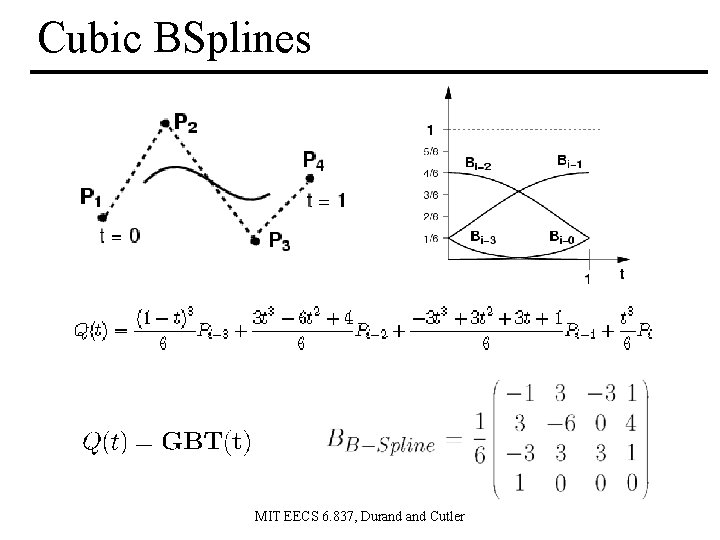
Cubic BSplines MIT EECS 6. 837, Durand Cutler

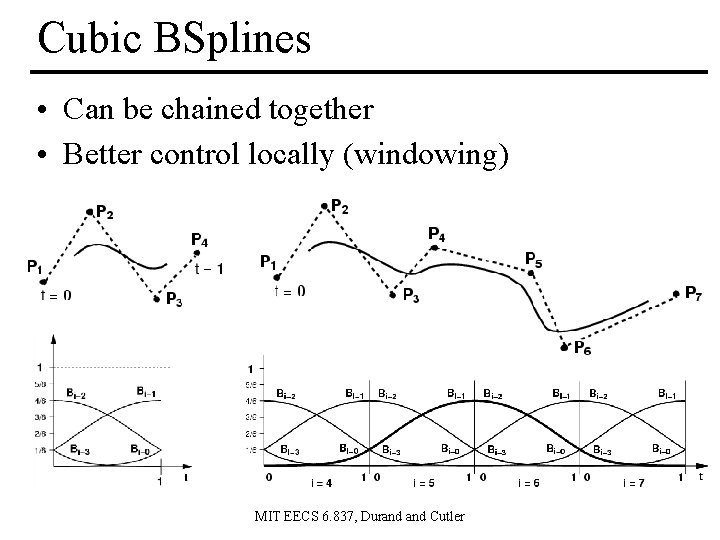
Cubic BSplines • Can be chained together • Better control locally (windowing) MIT EECS 6. 837, Durand Cutler

Bézier is not the same as BSpline Bézier BSpline MIT EECS 6. 837, Durand Cutler

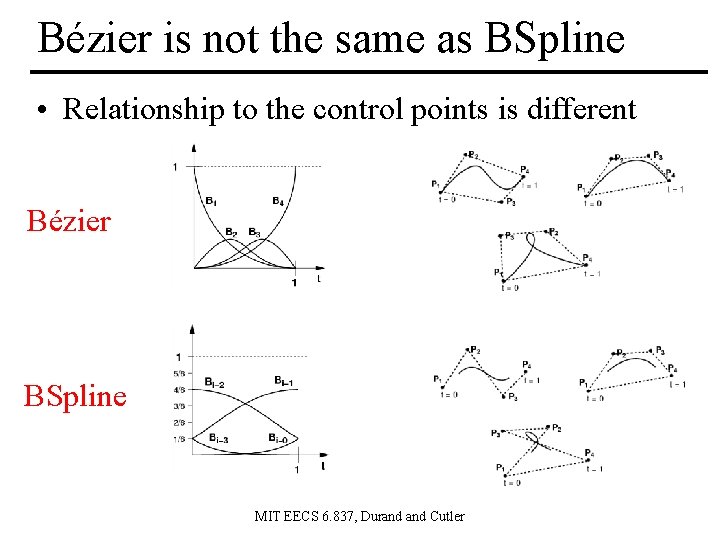
Bézier is not the same as BSpline • Relationship to the control points is different Bézier BSpline MIT EECS 6. 837, Durand Cutler

Converting between Bézier & BSpline new BSpline control points to match Bézier original control points as Bézier new Bézier control points to match BSpline MIT EECS 6. 837, Durand Cutler original control points as BSpline

NURBS (generalized BSplines) • BSpline: uniform cubic BSpline • NURBS: Non-Uniform Rational BSpline – non-uniform = different spacing between the blending functions, a. knots – rational = ratio of polynomials (instead of cubic) MIT EECS 6. 837, Durand Cutler

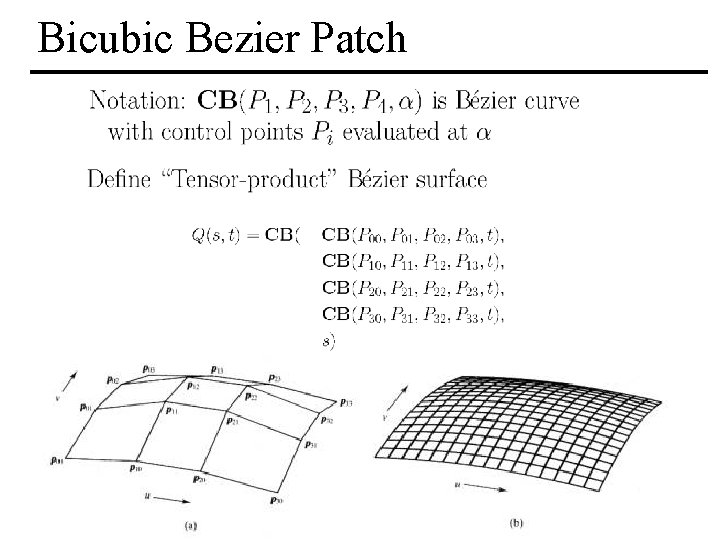
Bicubic Bezier Patch MIT EECS 6. 837, Durand Cutler

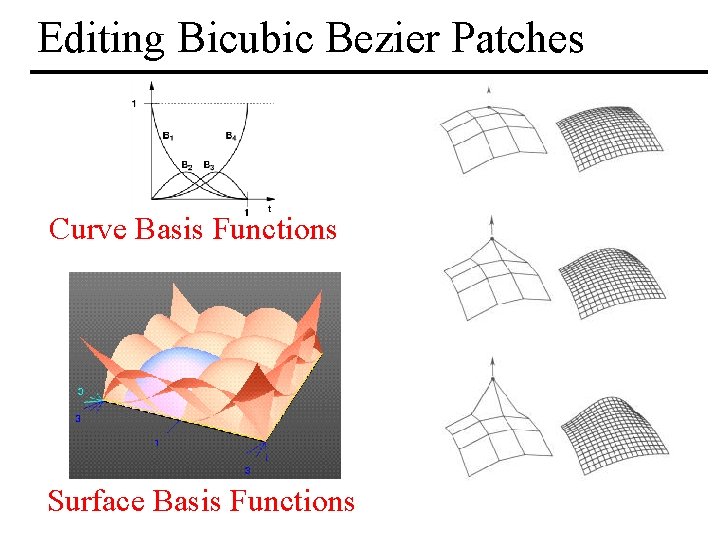
Editing Bicubic Bezier Patches Curve Basis Functions Surface Basis Functions MIT EECS 6. 837, Durand Cutler

Modeling with Bicubic Bezier Patches • Original Teapot specified with Bezier Patches MIT EECS 6. 837, Durand Cutler

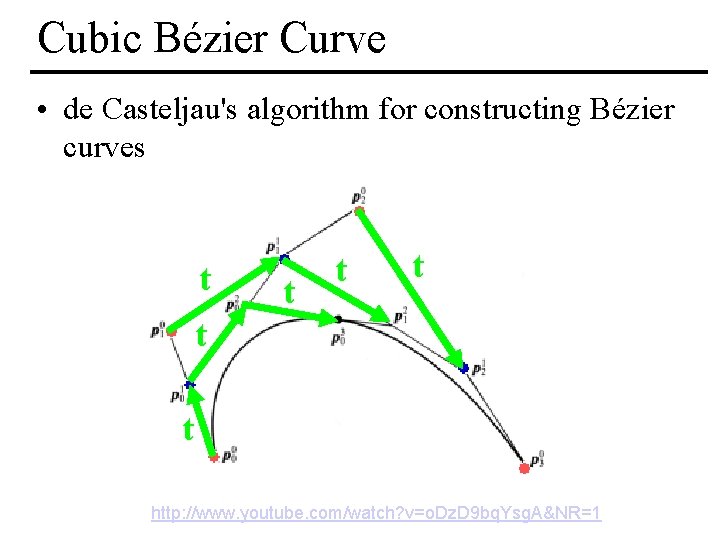
Cubic Bézier Curve • de Casteljau's algorithm for constructing Bézier curves t t t http: //www. youtube. com/watch? v=o. Dz. D 9 bq. Ysg. A&NR=1 MIT EECS 6. 837, Durand Cutler