Everyday Calculations www mathsrevision com NAT 3 Everyday





















- Slides: 25

Everyday Calculations www. mathsrevision. com NAT 3 Everyday Calculations Best Buys Rounding to nearest Whole Number Rounding to nearest Pence Tiling a Bathroom Wall 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

Starter Questions www. mathsrevision. com NAT 3 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

Everyday Calculations www. mathsrevision. com NAT 3 Learning Intention Success Criteria 1. We are learning about Everyday Calculations including Pay and Travel. 02 -Oct-20 1. Understand the terms pay and calculate simple wages. Created by Mr. Lafferty Maths Dept.

Everyday Calculations NAT 3 www. mathsrevision. com Example : Sean the mechanic hourly rate of pay is £ 6. 50. Last week he worked 38 hours. What is his basic pay? Pay is = £ 6. 50 x 38 = £ 247. 00 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

Everyday Calculations www. mathsrevision. com NAT 3 Example : Adam is a joiner his hourly rate of pay is £ 10. 50. He works 40 hours a week. What is his basic pay? Pay is = £ 10. 50 x 40 = £ 420. 00 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

Everyday Calculations www. mathsrevision. com NAT 3 Example : Liam’s yearly salary is £ 10800. How much does he get paid per month. Monthly Pay is 10800 ÷ 12 = £ 900 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

Total cost Everyday Calculations 46. 80 + 9. 90 = £ 56. 70 www. mathsrevision. com NAT 3 Example : A shirt cost £ 15. 60 and a tie costs £ 4. 95. What is the cost of 3 shirts and 2 ties ? £ 4 6. 8 0 02 -Oct-20 £ 9. 9 0 Created by Mr. Lafferty Maths Dept.

Everyday Calculations www. mathsrevision. com NAT 3 Example : A bunch of 48 bananas weighs 8 kilograms. How many bananas does this work out per kilogram. Per kilogram = 02 -Oct-20 Created by Mr. Lafferty Maths Dept. 6

Have you updated your Learning Log ? Wages & Salaries www. mathsrevision. com NAT 3 Now try Access Book Ex 9. 1 Ch 9 (page 105) 02 -Oct-20 Created by Mr. Lafferty Maths Department

Best Deals www. mathsrevision. com NAT 3 Learning Intention Success Criteria 1. We are learning about best deals. 02 -Oct-20 1. Be able to calculate best deal. Created by Mr. Lafferty Maths Dept.

Best Deals NAT 3 Example : www. mathsrevision. com 6 tins of Tomato soup cost £ 4. 20 at the supermarket. The local shop sells them for 75 p each. Which place is cheaper and by how much. £ 4. 5 0 02 -Oct-20 £ 0. 3 0 Created by Mr. Lafferty Maths Dept.

Best Deals NAT 3 £ 3 2 0 Example : www. mathsrevision. com Ewan the mechanic gets paid £ 1 100 a month. Joseph the bus driver gets paid £ 260 a week. Who gets the better annual salary and by how much. Mechanic : Annual Salary = £ 1 100 x 12 = £ 13 200 Bus Driver : Annual Salary = £ 260 x 52 = £ 13 520 Bus driver has better annual wage 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

Best Deals NAT 3 Example : www. mathsrevision. com A bunch of 5 bananas are on sale in Liam’s shop for £ 2. 25 Shannon’s Store has the same bananas at 6 for £ 2. 64. Which is the better store to buy the bananas. £ 0. 4 5 02 -Oct-20 £ 0. 4 4 Created by Mr. Lafferty Maths Dept.

Best Deals NAT 3 Example : www. mathsrevision. com Zakco store sells 6 metres of wood for £ 7. 20 Bryan store sells 7 metres for the same wood for £ 8. 75 Buy working out the price for 1 metre. Find cheapest store £ 1 02 -Oct-20 . 2 0 £ 1. 2 5 Created by Mr. Lafferty Maths Dept.

Best Deals www. mathsrevision. com NAT 3 Now try Ex 9. 2 Ch 9 (page 107) 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

Rounding to Nearest Unit www. mathsrevision. com NAT 3 Learning Intention Success Criteria 1. We are learning how to round to 1 decimal place. 02 -Oct-20 1. Remember steps to round to 1 decimal place. Created by Mr. Lafferty Maths Dept.

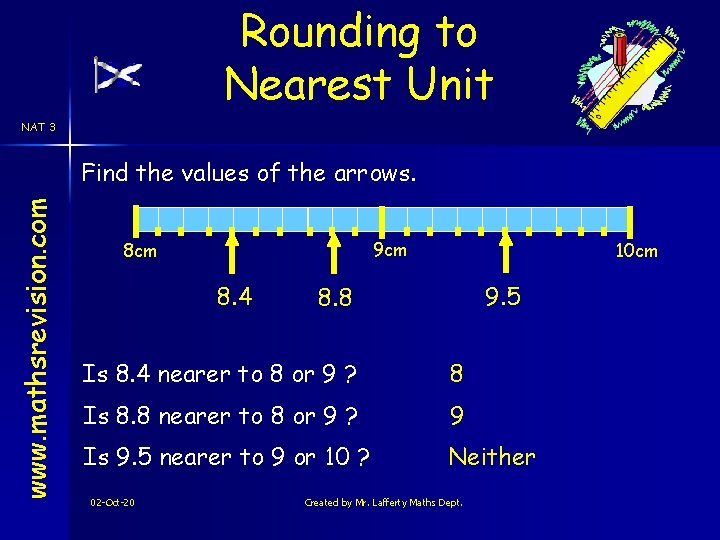
Rounding to Nearest Unit NAT 3 www. mathsrevision. com Find the values of the arrows. 9 cm 8. 4 10 cm 9. 5 8. 8 Is 8. 4 nearer to 8 or 9 ? 8 Is 8. 8 nearer to 8 or 9 ? 9 Is 9. 5 nearer to 9 or 10 ? Neither 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

Rounding to Nearest Unit www. mathsrevision. com NAT 3 If the 1 st decimal place is 0, 1, 2, 3, 4 – round down If the 1 st decimal place is 5, 6, 7, 8, 9 – round up Example : Round the numbers to the nearest unit (a) 9. 4 (b) 18. 8 (c) 24. 5 (d) 12. 3 (e) 102. 9 (f) 2636. 5 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

Nearest Unit www. mathsrevision. com NAT 3 Now try Ex 9. 3 Q 1 to Q 3 Ch 9 (page 109) 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

To the Nearest Pence www. mathsrevision. com NAT 3 When dealing with money we always round to 2 decimal places. The decimal part of the number is pence. Example £ 8. 24 means 8 pounds and 24 pence £ 3. 09 means 3 pounds and 9 pence 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

To the Nearest Pence NAT 3 www. mathsrevision. com If the 3 rd decimal place is 0, 1, 2, 3, 4 – round down If the 3 rd decimal place is 5, 6, 7, 8, 9 – round up Example : Round the money to the nearest pence. (a) £ 9. 043 (b) £ 18. 087 (c) £ 24. 254 (d) £ 12. 730 (e) £ 102. 093 (f) £ 2636. 555 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

To the Nearest Pence www. mathsrevision. com NAT 3 Now try Ex 9. 3 Q 4 to Q 11 Ch 9 (page 110) 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

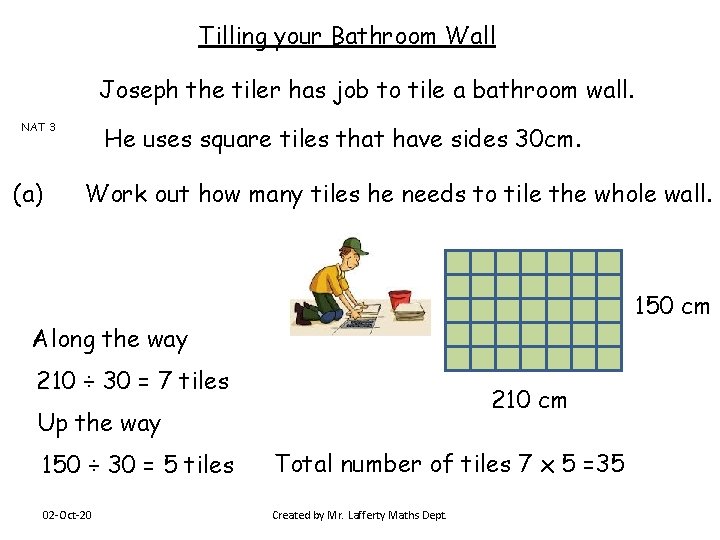
Tilling your Bathroom Wall Joseph the tiler has job to tile a bathroom wall. NAT 3 (a) He uses square tiles that have sides 30 cm. Work out how many tiles he needs to tile the whole wall. 150 cm Along the way 210 ÷ 30 = 7 tiles 210 cm Up the way 150 ÷ 30 = 5 tiles Total number of tiles 7 x 5 =35 02 -Oct-20 Created by Mr. Lafferty Maths Dept.

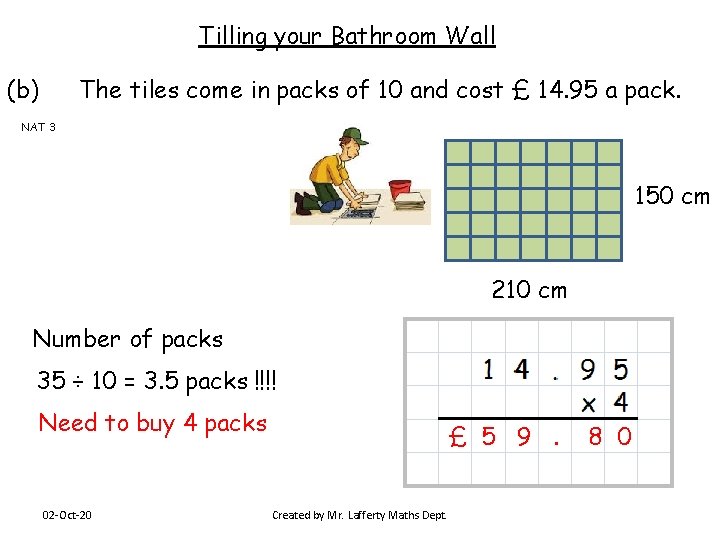
Tilling your Bathroom Wall (b) The tiles come in packs of 10 and cost £ 14. 95 a pack. NAT 3 150 cm 210 cm Number of packs 35 ÷ 10 = 3. 5 packs !!!! Need to buy 4 packs 02 -Oct-20 £ 5 9. Created by Mr. Lafferty Maths Dept. 8 0

Tiling Bathroom www. mathsrevision. com NAT 3 Now try Ex 9. 4 Ch 9 (page 111) 02 -Oct-20 Created by Mr. Lafferty Maths Dept.