Evaluation of water vapor diffusion equation solving schemes

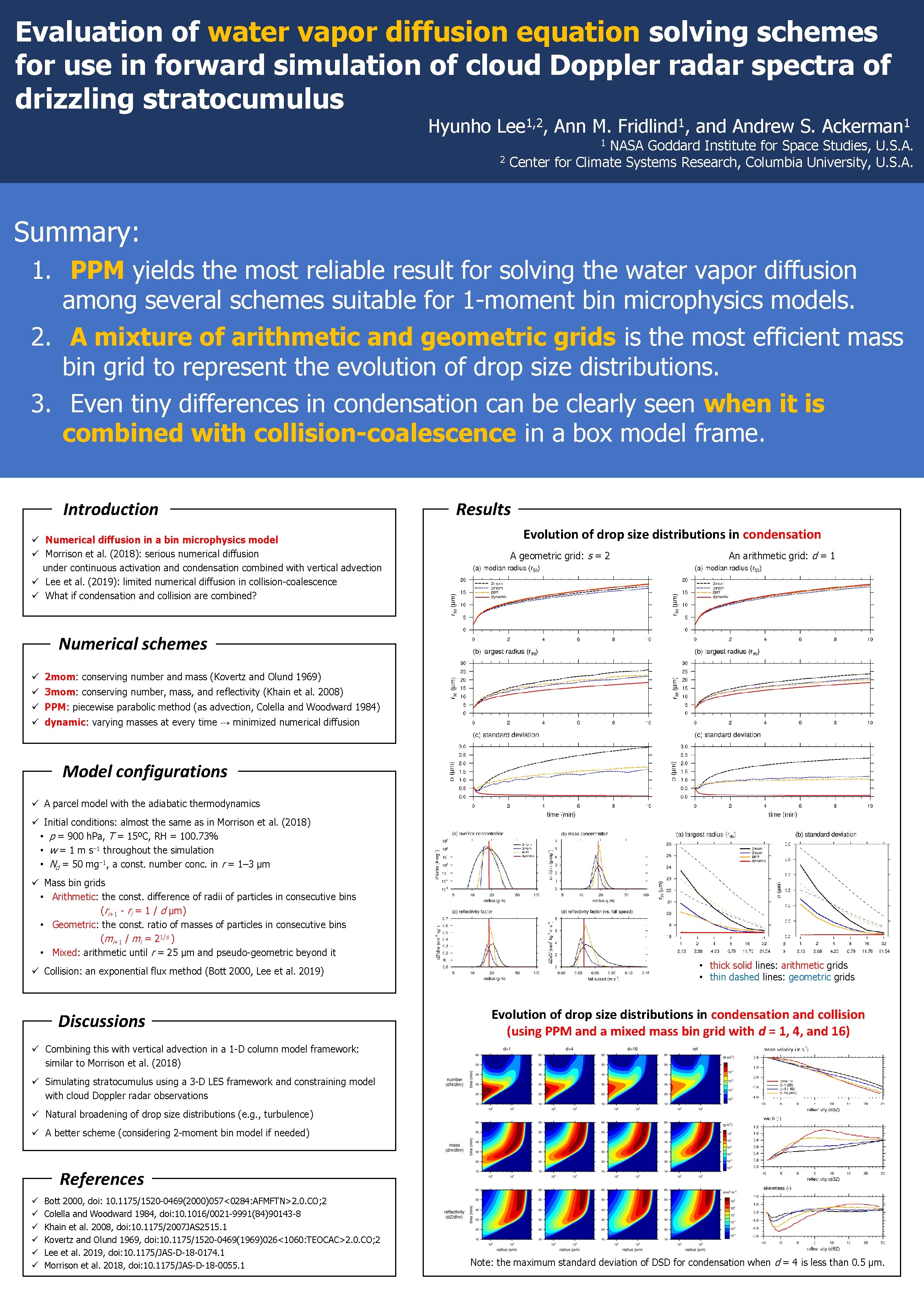
Evaluation of water vapor diffusion equation solving schemes for use in forward simulation of cloud Doppler radar spectra of drizzling stratocumulus Hyunho 1, 2 Lee , Ann M. 1 Fridlind , and Andrew S. 1 Ackerman NASA Goddard Institute for Space Studies, U. S. A. Center for Climate Systems Research, Columbia University, U. S. A. 1 2 Summary: 1. PPM yields the most reliable result for solving the water vapor diffusion among several schemes suitable for 1 -moment bin microphysics models. 2. A mixture of arithmetic and geometric grids is the most efficient mass bin grid to represent the evolution of drop size distributions. 3. Even tiny differences in condensation can be clearly seen when it is combined with collision-coalescence in a box model frame. Introduction ü Numerical diffusion in a bin microphysics model ü Morrison et al. (2018): serious numerical diffusion under continuous activation and condensation combined with vertical advection ü Lee et al. (2019): limited numerical diffusion in collision-coalescence ü What if condensation and collision are combined? Results Evolution of drop size distributions in condensation A geometric grid: s = 2 An arithmetic grid: d = 1 Numerical schemes ü 2 mom: conserving number and mass (Kovertz and Olund 1969) ü 3 mom: conserving number, mass, and reflectivity (Khain et al. 2008) ü PPM: piecewise parabolic method (as advection, Colella and Woodward 1984) ü dynamic: varying masses at every time → minimized numerical diffusion Model configurations ü A parcel model with the adiabatic thermodynamics ü Initial conditions: almost the same as in Morrison et al. (2018) • p = 900 h. Pa, T = 15ºC, RH = 100. 73% • w = 1 m s– 1 throughout the simulation • Nd = 50 mg– 1, a const. number conc. in r = 1– 3 μm ü Mass bin grids • Arithmetic: the const. difference of radii of particles in consecutive bins (ri+1 - ri = 1 / d μm) • Geometric: the const. ratio of masses of particles in consecutive bins (mi+1 / mi = 21/s ) • Mixed: arithmetic until r = 25 μm and pseudo-geometric beyond it ü Collision: an exponential flux method (Bott 2000, Lee et al. 2019) Discussions • thick solid lines: arithmetic grids • thin dashed lines: geometric grids Evolution of drop size distributions in condensation and collision (using PPM and a mixed mass bin grid with d = 1, 4, and 16) ü Combining this with vertical advection in a 1 -D column model framework: similar to Morrison et al. (2018) ü Simulating stratocumulus using a 3 -D LES framework and constraining model with cloud Doppler radar observations ü Natural broadening of drop size distributions (e. g. , turbulence) ü A better scheme (considering 2 -moment bin model if needed) References ü ü ü Bott 2000, doi: 10. 1175/1520 -0469(2000)057<0284: AFMFTN>2. 0. CO; 2 Colella and Woodward 1984, doi: 10. 1016/0021 -9991(84)90143 -8 Khain et al. 2008, doi: 10. 1175/2007 JAS 2515. 1 Kovertz and Olund 1969, doi: 10. 1175/1520 -0469(1969)026<1060: TEOCAC>2. 0. CO; 2 Lee et al. 2019, doi: 10. 1175/JAS-D-18 -0174. 1 Morrison et al. 2018, doi: 10. 1175/JAS-D-18 -0055. 1 Note: the maximum standard deviation of DSD for condensation when d = 4 is less than 0. 5 μm.