Evaluating Limits Algebraically AP Calculus Ms Olifer Objective

Evaluating Limits Algebraically AP Calculus Ms. Olifer Ø Objective: You will use the properties of limits to evaluate limits algebraically. Ø You will also evaluate limits involving infinity algebraically and conceptually.

Properties of Limits

Continuous Intervals Such functions are “well-behaved” functions on these intervals and their limits can be evaluated by direct substitution. *Note: All polynomial functions are “wellbehaved” functions and therefore are continuous on the interval

Limits of a Constant Value: (think about the graph) Evaluate each limit: These are continuous functions, so the direction that we are approaching doesn’t necessarily matter.

Limits of Polynomial Functions
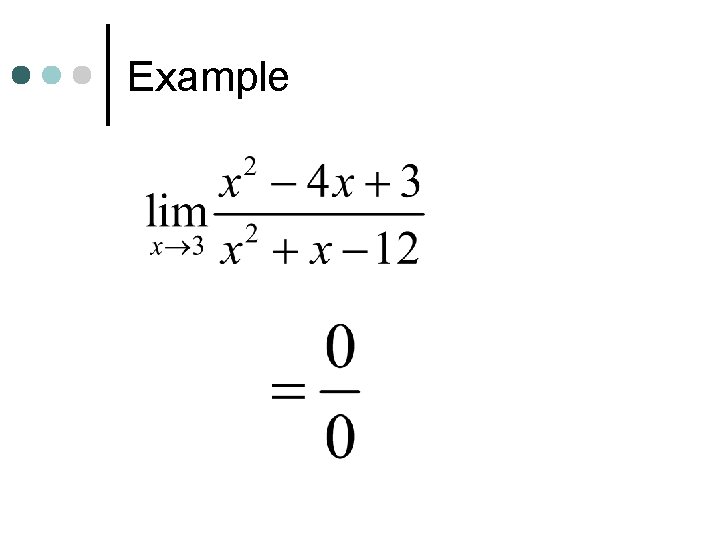
Example

Indeterminate Form ¢ We say that f(x) has an indeterminate form (or is indeterminate) at x = c if the formula for f(c) yields an undefined expression of the type

WHAT to DO? ? ? STRATEGY: ¢ Transform f(x) algebraically, if possible, into a new expression that is defined and continuous at x = c, and then evaluate the limit by substitution.
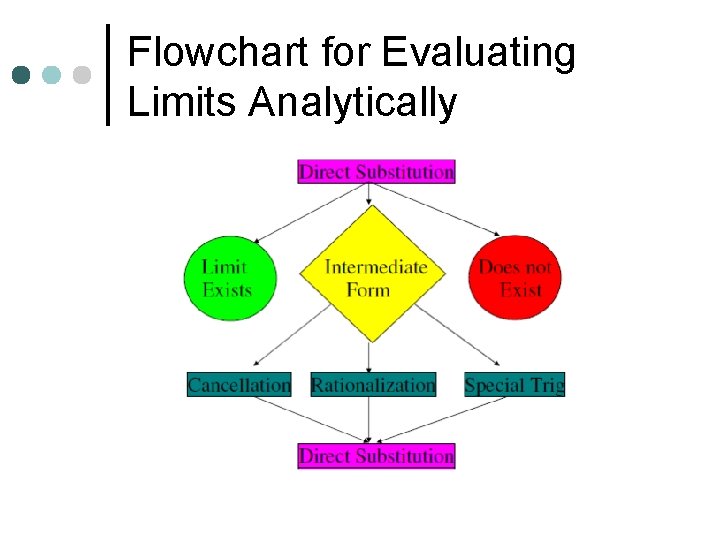
Flowchart for Evaluating Limits Analytically

Example (continued)


Multiplying by the Conjugate

Evaluate:


Infinite But Not Indeterminate ¢ Evaluate: Substitution leads to ¢ f(x) is not indeterminate at x = 2 ¢ Graph on pg. 93 ¢ ¢ Limit doesn’t exist

See y u t m rr w!
- Slides: 16