Eulers network theorem NodeVertice V Arc Lines L

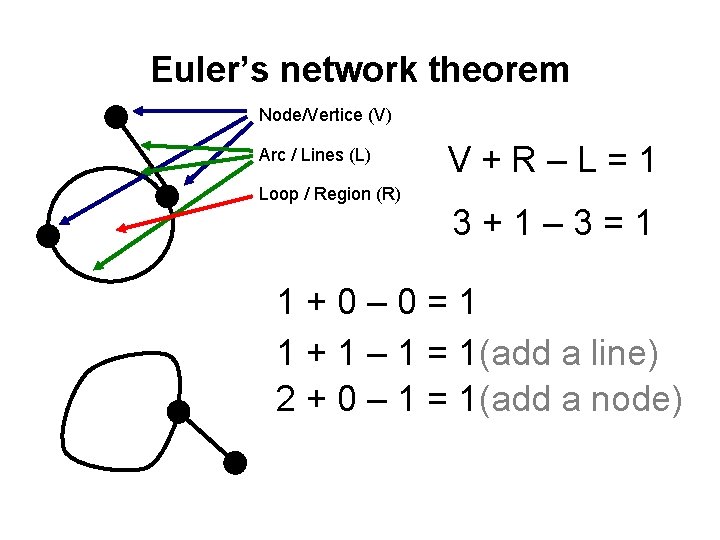
Euler’s network theorem Node/Vertice (V) Arc / Lines (L) Loop / Region (R) V+R–L=1 3+1– 3=1 1+0– 0=1 1 + 1 – 1 = 1(add a line) 2 + 0 – 1 = 1(add a node)

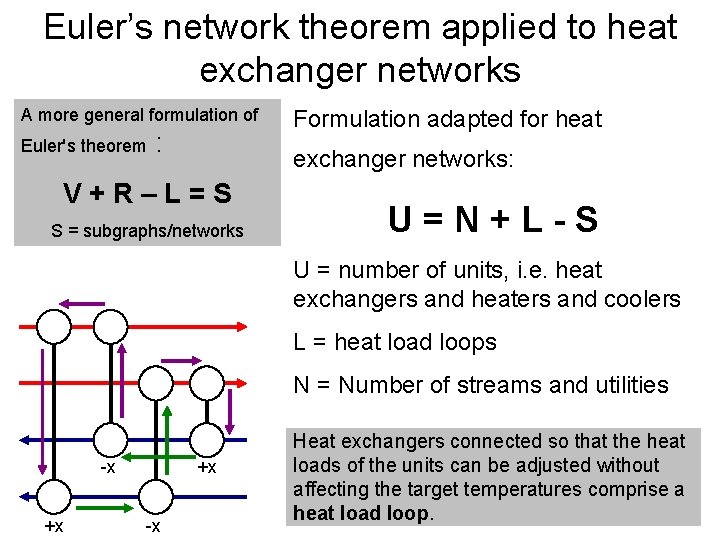
Euler’s network theorem applied to heat exchanger networks A more general formulation of Euler's theorem : Formulation adapted for heat exchanger networks: V+R–L=S S = subgraphs/networks U=N+L-S U = number of units, i. e. heat exchangers and heaters and coolers L = heat load loops N = Number of streams and utilities -x +x +x -x Heat exchangers connected so that the heat loads of the units can be adjusted without affecting the target temperatures comprise a heat load loop.

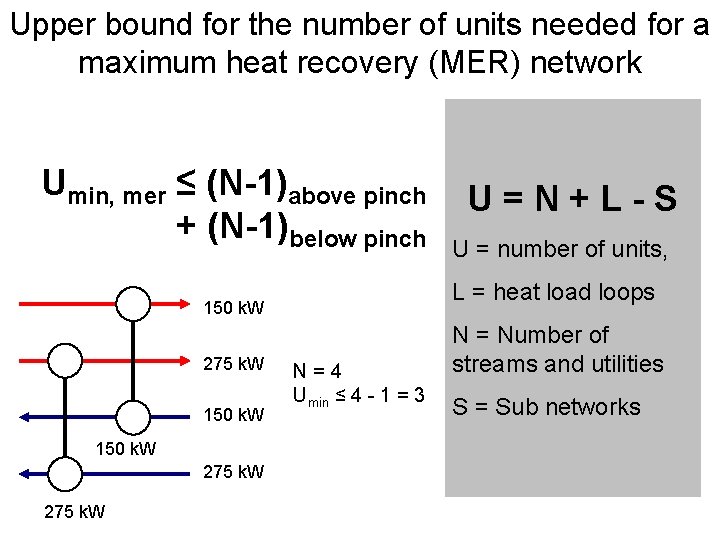
Upper bound for the number of units needed for a maximum heat recovery (MER) network Umin, mer ≤ (N-1)above pinch + (N-1)below pinch 150 k. W 275 k. W U = number of units, L = heat load loops 150 k. W 275 k. W U=N+L-S N=4 Umin ≤ 4 - 1 = 3 N = Number of streams and utilities S = Sub networks

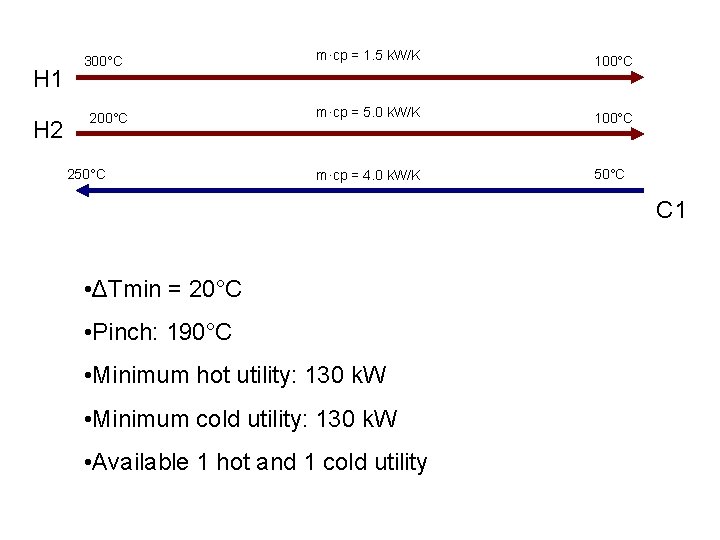
H 1 H 2 300°C 250°C m·cp = 1. 5 k. W/K 100°C m·cp = 5. 0 k. W/K 100°C m·cp = 4. 0 k. W/K 50°C C 1 • ΔTmin = 20°C • Pinch: 190°C • Minimum hot utility: 130 k. W • Minimum cold utility: 130 k. W • Available 1 hot and 1 cold utility

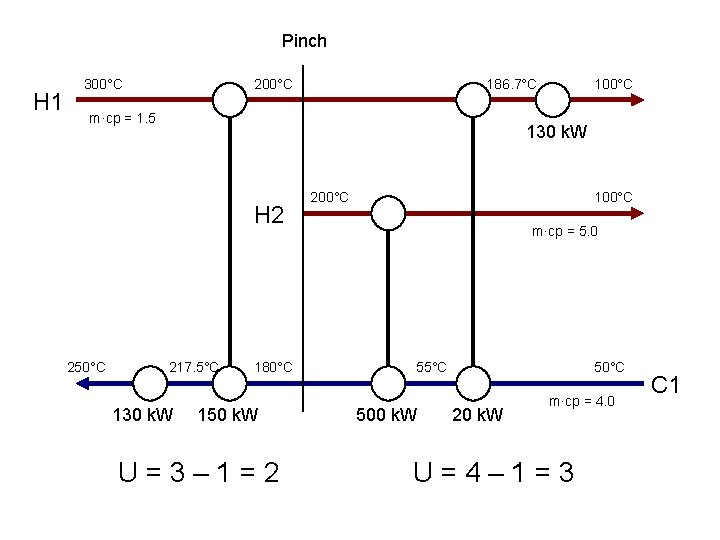
Pinch H 1 300°C 200°C 186. 7°C m·cp = 1. 5 130 k. W H 2 250°C 100°C 217. 5°C 130 k. W 180°C 150 k. W U=3– 1=2 200°C 100°C m·cp = 5. 0 55°C 500 k. W 50°C 20 k. W m·cp = 4. 0 U=4– 1=3 C 1

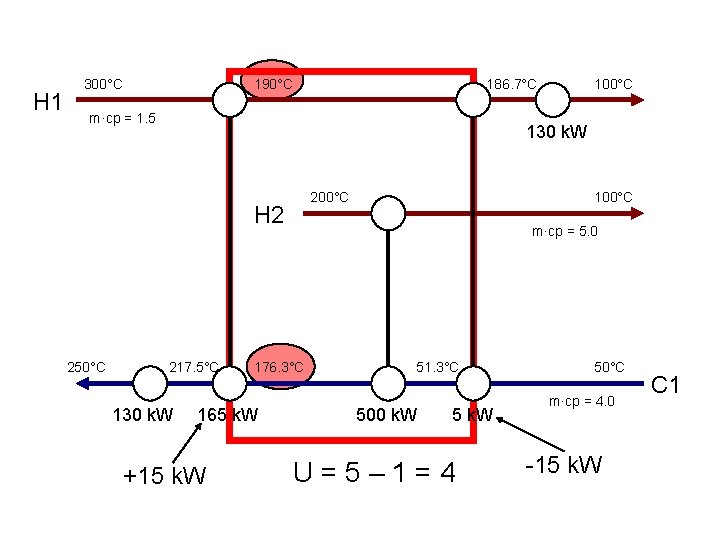
H 1 300°C 190°C 186. 7°C m·cp = 1. 5 130 k. W 200°C H 2 250°C 100°C 217. 5°C 130 k. W +15 k. W m·cp = 5. 0 176. 3°C 165 k. W 100°C 51. 3°C 500 k. W 5 k. W U=5– 1=4 50°C m·cp = 4. 0 -15 k. W C 1

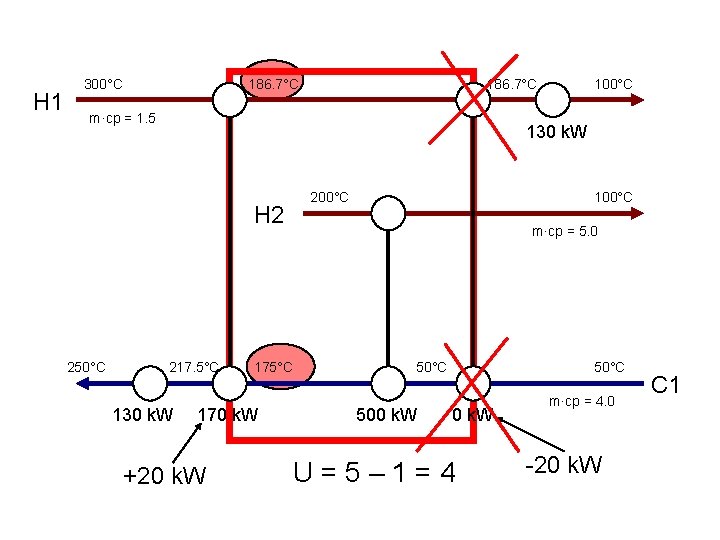
H 1 300°C 186. 7°C m·cp = 1. 5 130 k. W H 2 250°C 100°C 217. 5°C 130 k. W 175°C 170 k. W +20 k. W 200°C 100°C m·cp = 5. 0 50°C 500 k. W 50°C 0 k. W U=5– 1=4 m·cp = 4. 0 -20 k. W C 1

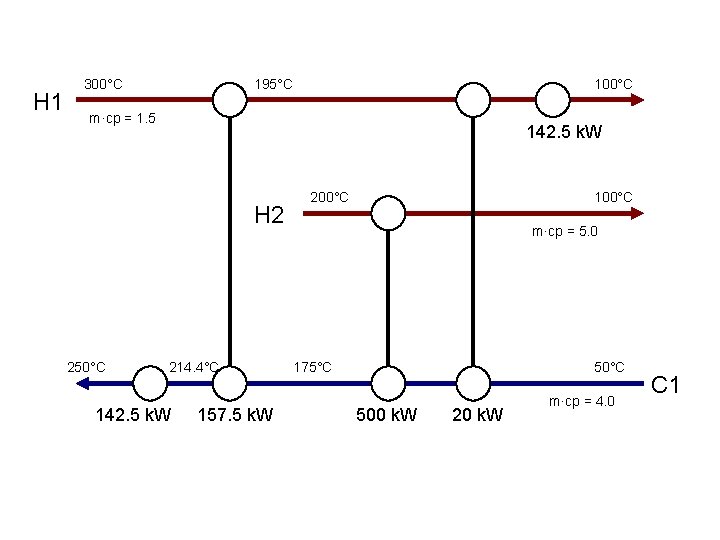
H 1 300°C 195°C 100°C m·cp = 1. 5 142. 5 k. W H 2 250°C 214. 4°C 142. 5 k. W 157. 5 k. W 200°C 100°C m·cp = 5. 0 175°C 500 k. W 20 k. W m·cp = 4. 0 C 1